Process Monitoring of Bivariate Poisson Data A Problem

Process Monitoring of Bivariate Poisson Data A Problem Oriented Solution Sotiris Bersimis, Department of Statistics and Insurance Science, University of Piraeus, Greece, and Petros E. Maravelakis, Department of Statistics and Actuarial. Financial Mathematics, University of the Aegean, Samos, Greece.

• Greek industry is composed of 23 sectors and the most important of them is the food and drink sector. • This sector represents about 21% of Greek manufacturing industry, includes more than 1, 300 enterprises and creates 70, 000 jobs. • In Crisis 2002, Greece’s food sector was second in the European rk of Economic Union (out of 15 countries), in terms of growth, reaching a growth rate of 3. 3% (in that period Spain hold the first place). • The first place in the food sector is taken by dairy products, products which hold 24%. • The 5 main sectors of the Greek dairy industry are: milk, milk yogurt, cheese, ice cream, cream and butter. The Problem is related to Food Industry

Contribution of Each Food Sector in the Greek Food Industry

• The dairy industry showed great signs of improvement, in the last 10 years, mainly because of the high nutritional value of dairy products and their close relationship with the Greek diet (now is also trapped in the economic crisis). • From the preceding discussion it is clear that the dairy industry is of great importance for Greek Economy while milk is of great importance for Greeks’ diet. • Among the different categories, Greeks prefer fresh milk, milk which holds 47. 4% of total share. • At the same time, all companies invest considerable money in terms of research and development, and installation of units to gather and process fresh milk of high quality and safety. quality safety In the dairy industry and Especially in Milk Production

• In fresh milk as well as in many food processing operations, product safety is controlled, by checking only the final product by microbiological and chemical methods (Tokatli et al, 2005). • A major drawback associated with this approach is time delay Collecting and examining the samples to determine the safety of the product takes too much time (the results of the microbiological analysis are completed only after the product is released to the market). market • Another drawback is that it can be a high-cost solution if any high-cost contamination is reported after the production is completed. Furthermore, the recall of the defective product and the collection from retail outlets add extra significant cost A Closer Look to the Problem

• Thus, it is clear that new process monitoring techniques are needed aiming at this type of problems • The significance of new process monitoring techniques to deal with this type of problems arises from the fact that these cases are related to public health, since there are many diseases associated with low quality milk (or similar food products): • • • Leptospirosis Cowpox. Tuberculosis Brucellosis Listeria Johne's Disease A Closer Look to the Problem

• A milk pasteurization plant. A continuous pasteurization line. • Our focus was concentered in the time interval after the pasteurization is completed and before the product is released to the consumer, since any pathogenic biological factor contained in the raw material is removed with the pasteurization process • What now if a pathogenic biological factor appears to the part of production after the pasteurization of the product? • As we already said microbiological methods are applied to the microbiological final product to ensure that the milk is safe for consumption. • But also we said that there is a time delay and that usually the exact results of the microbiological analysis are taken after the product is released to the market. The Exact Problem

• Thus we need a monitoring procedure ! • But what are we going to monitor ? • Usually in that case quality control departments monitor the percentage of the non-conforming products. • Also there are few cases that the quality control departments monitor the number of microorganisms of a specific type found in a sample (microorganisms per milliliter / in a suspension created by a sample from the production line)… • In that case we monitor with an appropriate control chart a Poisson distributed test statistic… • Note here that the milk (and almost all the food) contains microorganisms that if they do not exceed a threshold can not affect human health (in some cases are also useful). The Exact Problem

• But this needs time… • The Poisson based control chart is fed with measurements only after the product is at the hands of the consumer… • The quality managers are instructed that they have to wait a certain amount of time in order to proceed to the counting of microorganisms in the plate. • In that case, we are assuming that if a contamination factor exists, affects the new products in an increasing way (the effects are a function of time). • In that case, a better solution is to use CUSUM type or an EWMA control chart. The Exact Problem

• But the use of these types of charts do not solve the problem, because there is the time delay, and in that case an extreme event will identified only when is too late… • A better solution is to measure the number of microorganisms (of a specific type) that are developed in a test plate (created by a sample from the production line) in many time points …. • from zero point to the final time point (and not only at the end of the time period given in the microbiological guidelines). • In that way we may be capable to observe how fast are the number of microorganisms is growing. • The idea is that if a contaminating factor exists in the production line after the pasteurization process is completed then the number of microorganisms will be growing faster. The Exact Problem

• Also, if a contaminating factor make its appearance in the production line then it itself evolves (since it is a biological factor) causing continuously more and more contamination. • Thus, the proposed sampling procedure is the following: • Take one sample from the production line every k time units (say for example every 8 hours) • Define a value l for the measurements on microbiological system (say for example 6) – usually by Optical Density • If the guidelines instruct that the number of microorganisms of a specific type must measure in r hours (say 48 hours), then perform the 1 st test at the r/l (8 th) hour, the 2 nd test at the 2 r/l (16 th ) hour, …, and finally the lth test at the r (48 th ) hour. The Exact Problem

Sampling Point Plate / Interval 1 2 3 4 1 (0, 8] 2 (8, 16] 3 (16, 24] 4 (24, 32] 5 (32, 40] 6 (40, 48] 5 6 7 8 9 X(1, 1) X(1, 2) X(1, 3) X(1, 4) X(1, 5) X(1, 6) X(1, 7) X(1, 8) X(1, 9) 10 11 12 … …. …. X(2, 1) X(2, 2) X(2, 3) X(2, 4) X(2, 5) X(2, 6) X(2, 7) X(2, 8) X(2, 9) X(3, 1) X(3, 2) X(3, 3) X(3, 4) X(3, 5) X(3, 6) X(3, 7) X(3, 8) X(3, 9) …. X(4, 1) X(4, 2) X(4, 3) X(4, 4) X(4, 5) X(4, 6) X(4, 7) X(4, 8) X(4, 9) X(5, 1) X(5, 2) X(5, 3) X(5, 4) X(5, 5) X(5, 6) X(5, 7) X(5, 8) X(6, 1) X(6, 2) X(6, 3) X(6, 4) X(6, 5) X(6, 6) X(6, 7) • The null hypothesis is that the process is in control, that there is no time dependence, and that each of the components x(i, j), i=1, 2, …, l=6 and j=1, 2, …, +∞ follows a Poisson distribution with the parameter λl. • Thus, each time point u the sums of the form y(u)= x(1, u)+x(2, u-1)+…+x(l, u-l+1) are also Poisson random variables with parameter l∙λl. Sampling Scheme

• Thus, in case we are interested in only one type of bacterium, we may apply a univariate Shewhart type control chart on the statistic y(u)=x(1, u)+x(2, u-1)+…+x(l, u-l+1) for u=1, 2, …, +∞. Univariate Control Chart

• But what happens in the case that we have more than one types of bacterium ? Say for example 2. • In that case, we may apply the same technique in both the types of bacterium. • Thus, we conclude with two sums of the form • y(1, u)=x(1, u)+x(2, u-1)+…+x(l, u-l+1) for u=1, 2, …, +∞ • y(2, u)=x(1, u)+x(2, u-1)+…+x(l, u-l+1) for u=1, 2, …, +∞ • The two variables in most of the cases will be dependent, since the presence of a contaminating factor will trigger a chain reaction in the evolution of these types of bacterium. • In that case, we define the two dimensional random variable y=(y 1, y 2) which follows a two dimensional Poisson distribution with parameters λ 1, λ 2, and λ. The Bivariate Case

• The two dimensional random variable y=(y 1, y 2) has the following probability function • This bivariate setting is actually based on the joint distribution of the variables Y 1, Y 2 where in general Y 1=Z 1+Z 3 and Y 2=Z 2+Z 3 and Z 1, Z 2, Z 3 are mutually independent Poisson random variables with means λ 1, λ 2 and λ 3, respectively. The Bivariate Case

• The next step in our methodology is to identify the variable that will be used for the monitoring the bivariate process. • A fact that will be used to motivate the selection of this variable is that the number of the bacteria can only increase. Therefore, we are interested in a variable that will be able to detect fast this possible increase. • A straightforward selection is the sum of the two random variables Y 1 and Y 2 which is the sum of two dependent Poisson variables, say Y. • This random variable identifies an increase in the mean of either Y 1 and Y 2. • The random variable Y follows a Hermite distribution (see Jonshon, Kotz and Kemp (1992) pages 357 -364) with probability function The Bivariate Case

• Consequently, for the identification of an out of control situation we may construct a Shewhart type control chart with limits calculated using the Hermite distribution (see Montgomery (2008)). • This chart detects a possible increase in the mean of any of the two variables. Based on 1000 repetitions. The Bivariate Case Variable Shift 1 25% 1 75% 1 125% 2 75% 2 125% 1, 2 75% 1, 2 125% ATS Difference 82, 4 67, 1 22, 4 88, 2 65, 1 24, 1 52, 2 35, 2 20, 1

• The next step required by the nature of the problem is to see what happens after an out-of-control signal is given. • A method to identify the responsible variable is needed. • In order to identify the responsible variable after a signal we have to properly select a random variable that will help us in this direction. • Such a random variable is the difference of the two random variables Y 1 and Y 2, say Y’. • From the definition of the bivariate Poisson distribution we deduce that Y’=Y 1 -Y 2=Z 1 -Z 2, is the difference of two independent Poisson r. v. The Bivariate Case

• Since we use Y’ after a signal is issued, we expect to see one of the following results • a positive value of Y’ meaning that we have an increase in Z 1. • a negative value of Y’ meaning that we have an increase in Z 2. • a value of Y’ close to zero meaning that both Z 1 and Z 2 have shifted. • Therefore, the use of Y’ assures us that we will be able to identify the responsible variable in most of the cases. The probability distribution of Y’ is known and is given in Jonshon, Kotz and Kemp (1992) pages 190 -192 and it is of the form The Bivariate Case

• Thus, we may use the distribution of Y’ in order to define a formal procedure for identifying the out-of-control variable. • Specifically, if the value of Y’ is above the 95% percentage point of its theoretical distribution, then responsible variable is Y 1 and if the value of Y’ is below the 5% percentage point of its theoretical distribution then Y 2 is the responsible variable and if the value of is between the 5% and 95% percentage point of its theoretical distribution then both variables have shifted. The Bivariate Case

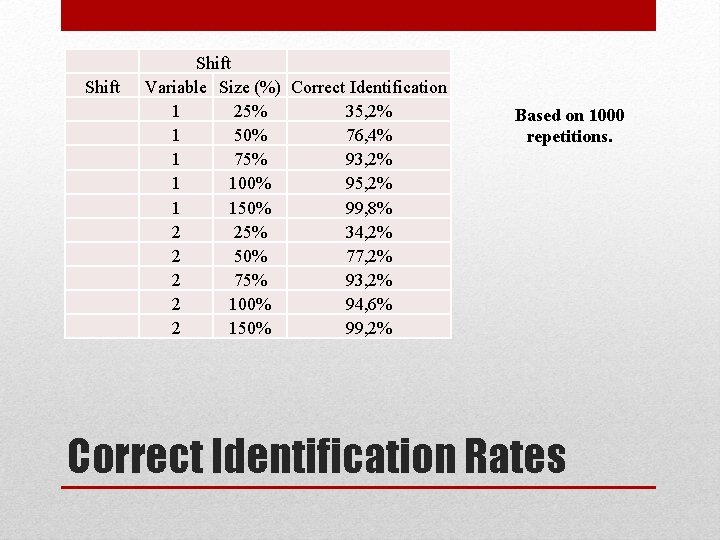
Shift Shift Variable Size (%) Correct Identification 1 25% 35, 2% 1 50% 76, 4% 1 75% 93, 2% 1 100% 95, 2% 1 150% 99, 8% 2 25% 34, 2% 2 50% 77, 2% 2 75% 93, 2% 2 100% 94, 6% 2 150% 99, 2% Based on 1000 repetitions. Correct Identification Rates

• Figen (Kosebalaban) Tokatli, Ali Cinar, Joseph E. Schlesser (2005). HACCP with multivariate process monitoring and fault diagnosis techniques: application to a food pasteurization process, Food Control, 16, 411– 422. • Jonshon, N. L. , Kotz, S. and Kemp, A. W. (1992). Univariate Discrete Distributions, Wiley, New York. • Montgomery, D. C. (2008). Introduction to Statistical Quality Control, Wiley, New York. References