PROCESS EQUIPMENT DESIGN GAS ADSORPTION COLUMN Problem Statement

PROCESS EQUIPMENT DESIGN GAS ADSORPTION COLUMN

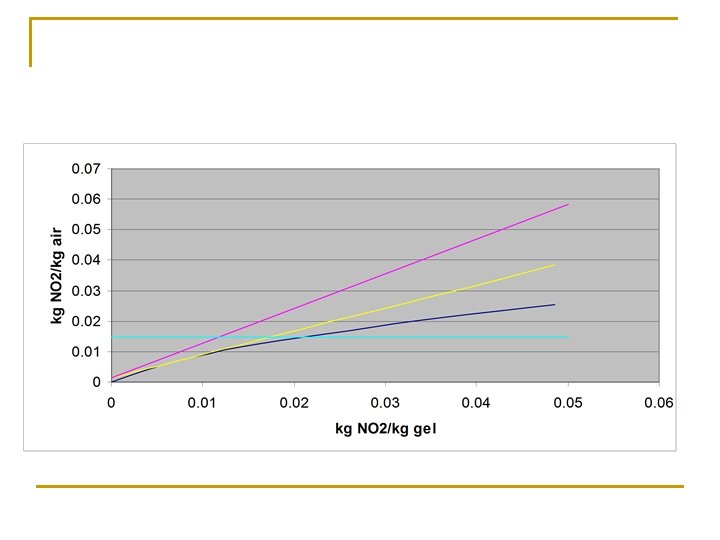
Problem Statement Nitrogen dioxide is produced by a thermal process is to be removed from a dilute mixture with air by adsorption on silica gel in a continuous counter current adsorber. The gas flow rate is 1000 lb/m 2 hr and contains 1. 5% NO 2 by volume. It is desired to remove 90% of the NO 2. Experimental data for equilibrium adsorption isotherm at 25 °C and 1 atm is given Partial pressure NO 2, mm Hg 0 2 4 6 8 10 12 Kg NO 2/ 100 kg gel 0 0. 4 0. 9 1. 65 2. 6 3. 65 4. 85

The silica gel has an average particle size of 0. 068 inches in diameter and external surface of particle is 10. 58 sq ft/lb. the individual resistance to mass transfer in fluid and within solid during adsorption of water vapor from air by silica gel are Kya. P = 188 G 0. 55 lb. H 20/ hr cu ft Ksa. P = 217 lb. H 20/ hr cu ft where G is the mass velocity of gas.

Adsorption n Process that occurs when a gas or liquid solute accumulates on the surface of a solid or more rarely, a liquid (adsorbent), forming a molecular or atomic film (the adsorbate). The term sorption encompasses both processes, while desorption is the reverse process. n Silica gel is a highly porous solid adsorbent material. It has a very large internal surface composed of myriad microscopic cavities and a vast system of capillary channels.

Conveying of Silica Gel n n Silica Gel is characterized as a B 28 material Possible methods 1. 2. 3. Belt conveyor: Costlier Bucket elevator Screw Conveyor Ø Ø Ø Screw dia: 12 in. Approximate area covered by materials: 15% Costing depends on correlation of manufacture

Regeneration of Adsorbent n n Thermal Pressure based Using Inert gas Steam condensation

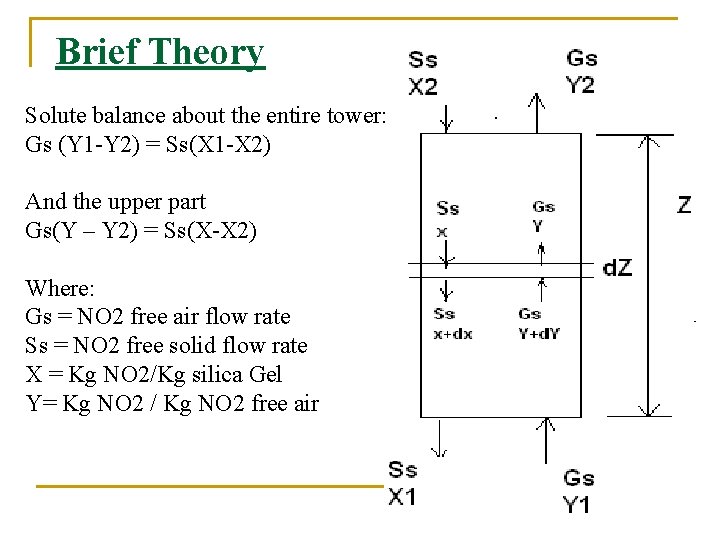
Brief Theory Solute balance about the entire tower: Gs (Y 1 -Y 2) = Ss(X 1 -X 2) And the upper part Gs(Y – Y 2) = Ss(X-X 2) Where: Gs = NO 2 free air flow rate Ss = NO 2 free solid flow rate X = Kg NO 2/Kg silica Gel Y= Kg NO 2 / Kg NO 2 free air

Solution Procedure n n n Fix (X 2, Y 2) by the specifications of the problem and the ordinate Y 1 Draw a tangent through (X 2, Y 2) to the equilibrium curve. This gives the minimum adsorbent rate required We operate at around 1 -1. 5 times the minimum rate We then assume, for ease of calculations, the equilibrium curve to be a straight line for the range of values that are encountered in the problem. Calculate Nt. OG and Ht. OG and hence Z

Resistances to mass transfer Gas phase resistance Liquid phase resistance = 217 lb. NO 2/ hr cu ft

Evaluation of height of tower (Z)

Results 1. 2. 3. 4. 5. 6. Minimum solid to gas ratio = 0. 76 Minimum adsorbent required = 1. 009 Kg/m 2. sec Actual adsorbent rate = 1. 52 Kg/m 2. sec Nt. OG = 4. 6 Ht. OG= 2. 54 m Z = 11. 6 m

References 1. 2. Mass Transfer Operations, by Robert E. Treybal, Third edition, Mc. Graw Hill Book Company. Chemical Engineers Handbook, Perry, R. H. , and C. H. Chilt 5 th Ed. Mc. Graw-Hill, NY, USA 3. Analysis of the Adsorption Process and of Desiccant Cooling Systems -A Pseudo-steady state Model for Coupled Heat and Mass Transfer, Robert S Barlow, 1982 4. Gas purification processes, Nonhebel G, George Newnes Limited, London

Thank You