PROCESS CONTROL PDT 255 Week 10 Second order

PROCESS CONTROL PDT 255 Week 10: Second order system response damping Wan Mastura Wan Ibrahim 1

Revision from last week Time constant - the speed with which the measured Process Variable (PV) responds to changes in the Controller Output (CO) 2

What is second order system? Second-order systems are described by a secondorder differential equation that relates the ouput variable y to the input variable x (the forcing function) with time as the independent variable.

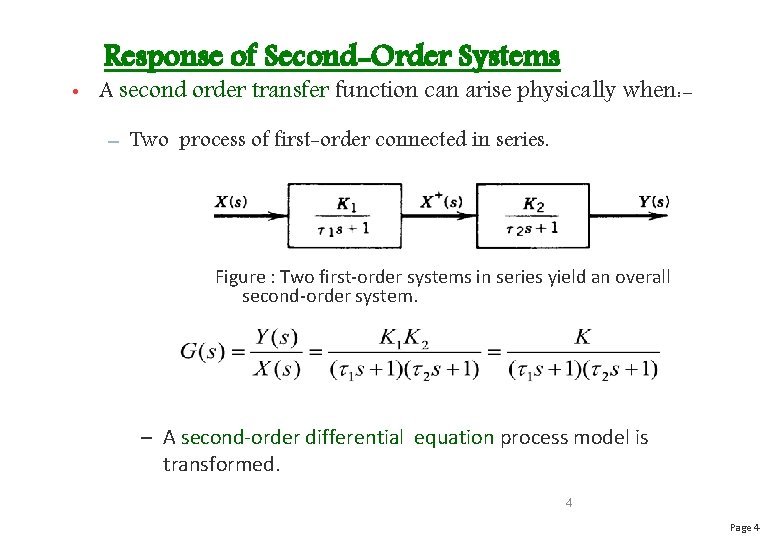
Response of Second-Order Systems • A second order transfer function can arise physically when: – Two process of first-order connected in series. Figure : Two first-order systems in series yield an overall second-order system. – A second-order differential equation process model is transformed. 4 Page 4

Second-order systems u Time-domain representation: Laplace-domain representation: K = process gain = natural period = damping coefficient Page 5

Standard form of the second-order transfer function. Where: is the process gain. is the time constant which determines the speed of response of the system. is the damping factor which provides a measure of the amount of damping in the system, that is, the degree of oscillation in a process response after a perturbation. 6

• Example 1: • Given the transfer function as shown below, find ζ and wn. • Solution • Compare with the general second-order transfer function, • therefore, a) b)

Example 2: Determining the Parameters of a 2 nd Order System from its Gp(s) 8

9

Exercise 1

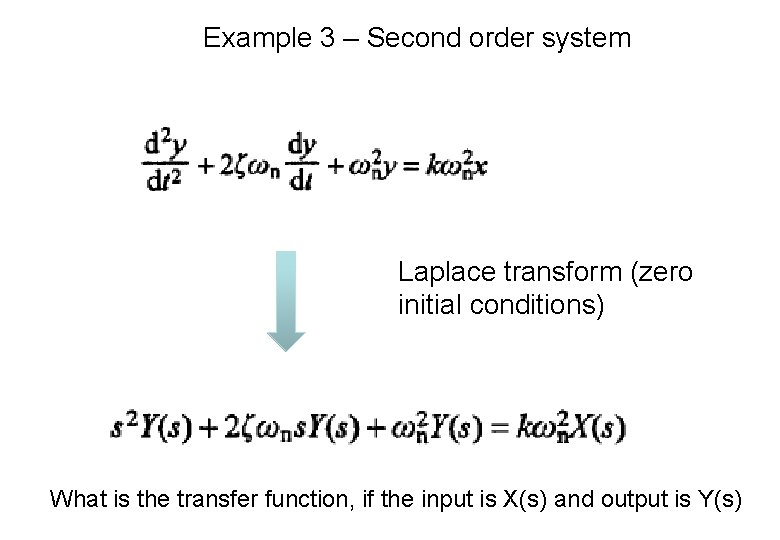
Example 3 – Second order system Laplace transform (zero initial conditions) What is the transfer function, if the input is X(s) and output is Y(s)

Example 3 – Continued Given that the input is a unit step input, what the output will be? Find the Laplace transform of a step input from your Laplace transformation table

Example 3 – Continued Unit step input, X(s) = 1/s Therefore, the output transform Y(s) is: • There are three different forms of answer to this equation for the way output varies with time – depends on value of damping constant, ζ • The system can be: overdamped, critically damped or underdamped

Example 3 – Continued The next step to know whether system is overdamped, critically damped or undamped – where p 1 and p 2 are the roots of the denominator quadratic term

Example 3 – Continued Let’s look back at our problem: How do we find roots of the equation? this is the CHARACTERISTIC EQUATION

Example 3 – Continued Please recall – formula to find roots of quadratic equation: Apply the formula to our equation The important issue in determining the form of the roots is the value of the square root term and this is determined by the value of the damping factor, ζ

Remember: The value of completely determines the degree of oscillation in a process response after a perturbation

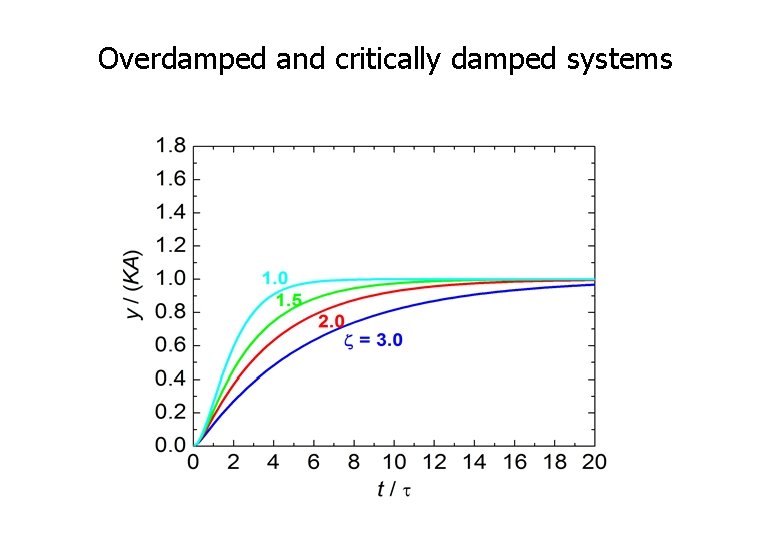
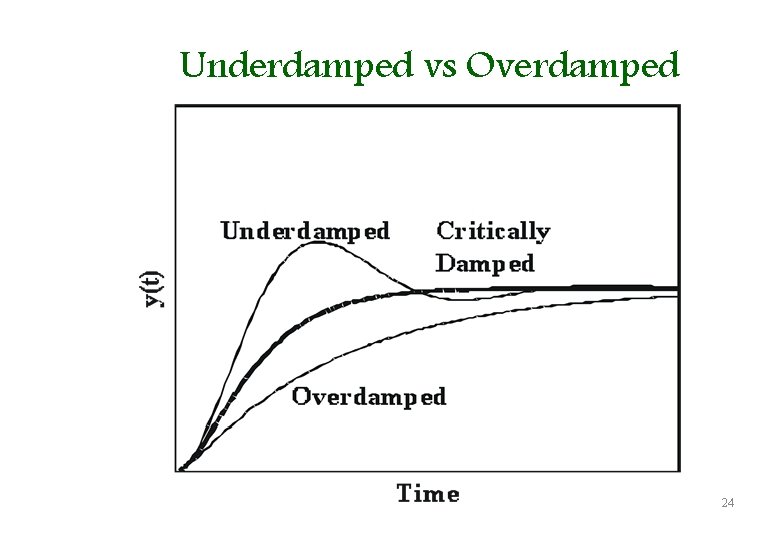
Case 1: ζ > 1 • The square root term (in previous slide) is real and will factorise • This describes an output which does not oscillate but dies away with time • The output takes longer than critical damping to reach the steady state value. • The system is called OVERDAMPED • As time tends to infinity, the output becomes steady

Overdamped and critically damped systems

Case 2: ζ = 1 • The square root term is zero • Both roots are real and both the same • This is called as CRITICALLY DAMPED condition – describing an output which does not oscillate but dies away with time • There is no oscillations and the output just gradually approaches the steady state value.

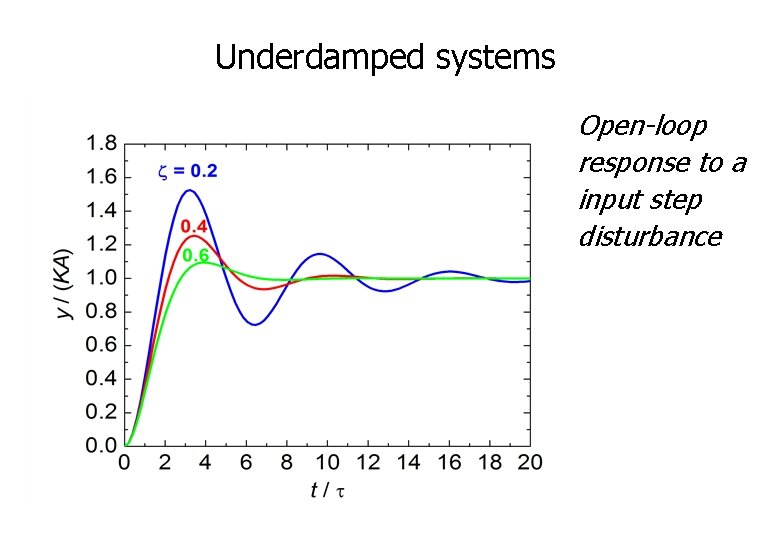
Case 3: 0 < ζ < 1 • The output is oscillates but the closer the damping ratio to 1 the faster the amplitude of the oscillations diminishes. • The square root term does not have a real value • The system is UNDERDAMPED • When the damping ratio is 0, the system is UNDAMPED Case 4: ζ < 0 • The system is unstable

Underdamped systems Open-loop response to a input step disturbance

Step Response of Second-Order Transfer Function - SUMMARY 4 is unstable second-order system that would have an unbounded response to any input. 23

Underdamped vs Overdamped 24

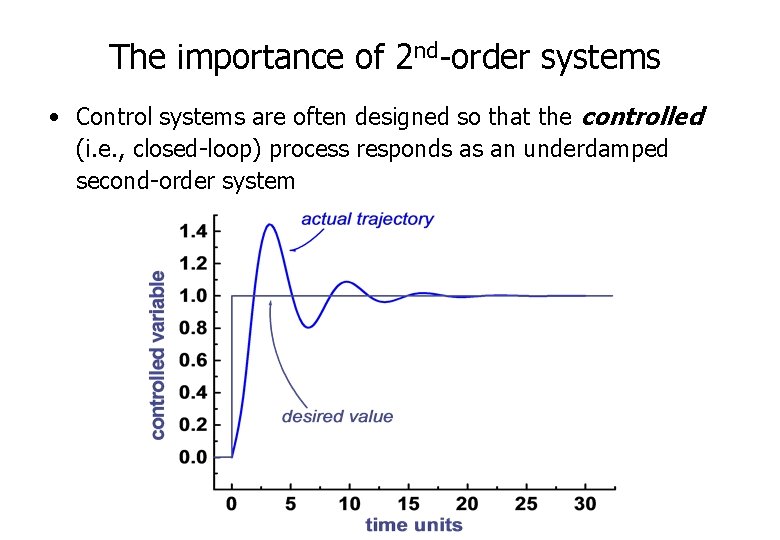
The importance of 2 nd-order systems • Control systems are often designed so that the controlled (i. e. , closed-loop) process responds as an underdamped second-order system

Example 4 How to solve: 1. Write how input, output and transfer function related 2. Find what is Laplace transform of the input 3. Find output 4. Find characteristic equation 5. Find roots of the characteristic equation

Exercise 2

References • Bolton, W. , Instrumentation and Control Systems. Norfolk, Newnes, 2004. • Seborg et al. Process dynamics and control • Coughanowr, D. , Le. Blanc, S. Process Systems Analysis and Control.