Process Control Laboratory 7 7 0 7 1

Process Control Laboratory 7. 7. 0 7. 1 7. 2 7. 3 7. 4 7. 5 7. 6 7. 7 7. 8 7. 9 KEH PID Controllers Overview PID controller variants Choice of controller type Specifications and performance criteria Controller tuning based on frequency response Controller tuning based on step response Model-based controller tuning Controller design by direct synthesis Internal model control Model simplification Process Dynamics and Control 7– 1

7. PID Controllers Process Control Laboratory 7. 0 Overview PID controller (”pee-i-dee”) is a generic name for a controller containing a linear combination of § proportional (P) § integral (I) § derivative (D) terms acting on a control error (or sometimes the process output). All parts need not be present. Frequently I and/or D action is missing, giving a controller like § P, PI, or PD controller It has been estimated that of all controllers in the world § 95 % are PID controllers KEH Process Dynamics and Control 7– 2

7. PID Controllers Process Control Laboratory 7. 1 PID controller variants 7. 1. 1 Ideal PID controller KEH Process Dynamics and Control 7– 3

7. 1. 1 Ideal PID controller 7. 1 PID controller variants Process Control Laboratory KEH Process Dynamics and Control 7– 4

7. 1 PID controller variants 7. PID Controllers Process Control Laboratory 7. 1. 2 The series form of a PID controller KEH Process Dynamics and Control 7– 5

7. 1 PID controller variants 7. PID Controllers Process Control Laboratory 7. 1. 3 A PID controller with derivative filter KEH Process Dynamics and Control 7– 6

7. 1 PID controller variants 7. 1. 3 A PID controller with derivative filter Process Control Laboratory KEH Process Dynamics and Control 7– 7

7. 1 PID controller variants 7. PID Controllers Process Control Laboratory 7. 1. 4 Differentiation of the measured output KEH Process Dynamics and Control 7– 8

7. 1. 4 Differentiation of the measured output 7. 1 PID controller variants Process Control Laboratory 7. 1. 5 Setpoint weighting KEH Process Dynamics and Control 7– 9

7. 1. 5 Setpoint weighting 7. 1 PID controller variants Process Control Laboratory KEH Process Dynamics and Control 7– 10

7. 1 PID controller variants 7. PID Controllers Process Control Laboratory 7. 1. 6 Non-interactive form of a PID controller KEH Process Dynamics and Control 7– 11

7. PID Controllers Process Control Laboratory 7. 2 Choice of controller type 7. 2. 1 On-off controller KEH Process Dynamics and Control 7– 12

7. PID Controllers Process Control Laboratory 7. 2 Choice of controller type 7. 2. 2 P controller KEH Process Dynamics and Control 7– 13

7. PID Controllers Process Control Laboratory 7. 2 Choice of controller type 7. 2. 3 PI controller KEH Process Dynamics and Control 7– 14

7. 2 Choice of controller type 7. PID Controllers Process Control Laboratory 7. 2. 4 PD controller KEH Process Dynamics and Control 7– 15

7. 2 Choice of controller type 7. PID Controllers Process Control Laboratory 7. 2. 5 PID controller KEH Process Dynamics and Control 7– 16

7. PID Controllers Process Control Laboratory 7. 3 Specifications and performance criteria 7. 3. 1 General performance criteria The task of a controller is to control a system to behave in a desired way despite unknown disturbances and an inaccurately known system. The controlled system should satisfy performance criteria such as: § The controlled system must be stable; this is absolutely necessary. § The effect of disturbances on the controlled output is minimized; this is especially important for regulatory control. § The controlled output should follow setpoint changes fast and smoothly; this is especially important for setpoint tracking. § The control error is minimized or kept within certain limits, § The control signal variations should be moderate or at least not be excessively large; more variations wear out control equipment faster. § The control system should be robust (insensitive) against moderate changes in system properties, which introduce model uncertainty. The importance of these criteria varies from case to case. Since many criteria are conflicting, compromises have to be made in the control design. KEH Process Dynamics and Control 7– 17

7. PID Controllers Process Control Laboratory 7. 3 Specifications and performance criteria 7. 3. 2 Fundamental limitations One reason to the fact that there are usually good solutions to the conflicting control criteria is that feedback control is used. § However, feedback also introduces limitations because a control error is required for the controller to take action. § The fact that the available resources for control are always limited, also limit the achievable performance. In addition to the general limitations above, there also limitations that depend on the process to be controlled, e. g. , § the dynamics of the process § nonlinearities § model and process uncertainty § disturbances § control signal limitations KEH Process Dynamics and Control 7– 18

7. 3 Specifications and performance criteria Process Control Laboratory 7. 3. 2 Fundamental limitations The process dynamics is often the performance limiting factor. Such factors are § time delays as well as RHP (right-half plane) poles and zeros § high-order dynamics In practice, all processes are nonlinear. Such a process § cannot be described accurately at different operating points by a linear model with constant parameters; thus there is model/process uncertainty. Disturbances such as load disturbances and measurement noise limit how well a variable can be controlled. § Efficient control of load disturbances often require derivative action, but measurement noise is bad for the derivative. § Large load disturbances can cause the control variable to reach its (physical) maximum or minimum value. This is especially troublesome if the controller contains an integrator. Proportional band integrator windup are two concepts that deal with this limitation. KEH Process Dynamics and Control 7– 19

7. PID Controllers Process Control Laboratory 7. 3 Specifications and performance criteria 7. 3. 3 Proportional band integrator windup KEH Process Dynamics and Control 7– 20

7. 3. 3 Proportional band integrator windup Proportional band Process Control Laboratory KEH Process Dynamics and Control 7– 21

7. 3 Specifications and performance criteria Process Control Laboratory 7. 3. 3 PB and integrator windup Integrator windup Usually controllers are tuned for stability and performance, not for signal limits. Therefore, it is not uncommon that a control signal reaches a constraint. If the controller contains integral action, this can be very damaging to the control performance unless the situation is handled properly. Consider the figure, where the PI control law (7. 25) has been used. A strong disturbance causes the process output to fall well below the setpoint. The controller is not able to eliminate the control error (A) because the control signal has reached a constraint. During this time, the positive control error will increase the integral in the controller. If the disturbance later disappears, the controller will still keep the control signal at the constraint due to the large value of the integral, even if the control error goes below zero. This will cause the output (B), which is entirely due to the controller. Illustration of integral windup. KEH Process Dynamics and Control 7– 22

7. 3. 3 Proportional band integrator windup Integral windup The described phenomenon is called integral windup (also reset windup). Process Control Laboratory There are sophisticated as well as simple methods for handling the problem. The term anti-windup is used for such arrangements. A simple solution is to stop integrating when a control signal reaches a constraint. This requires that § it is known when the control signal reaches a constraint (e. g. , through measurement) § there is some built-in logic to interrupt the integration In the case of digital control, which nowadays is customary, automatic anti-windup can be built into the control law. KEH Process Dynamics and Control 7– 23

7. PID Controllers Process Control Laboratory 7. 3 Specifications and performance criteria 7. 3. 4 Design specifications KEH Process Dynamics and Control 7– 24

7. 3. 4 Design specifications Step-response specifications Process Control Laboratory KEH Process Dynamics and Control 7– 25

7. 3 Specifications and performance criteria 7. 3. 4 Design specifications Process Control Laboratory KEH Process Dynamics and Control 7– 26

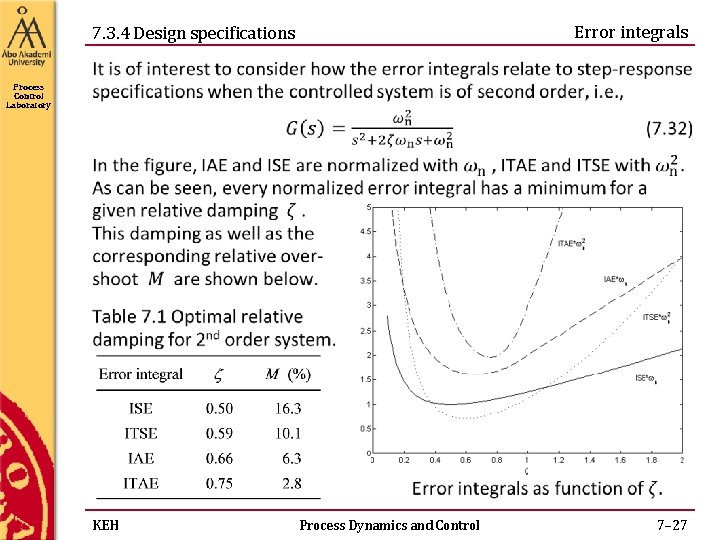
Error integrals 7. 3. 4 Design specifications Process Control Laboratory KEH Process Dynamics and Control 7– 27

7. PID Controllers Process Control Laboratory 7. 4 Tuning based on frequency response 7. 4. 1 Experimental tuning KEH Process Dynamics and Control 7– 28

7. 4 Tuning based on frequency response 7. 4. 1 Experimental tuning Process Control Laboratory KEH Process Dynamics and Control 7– 29

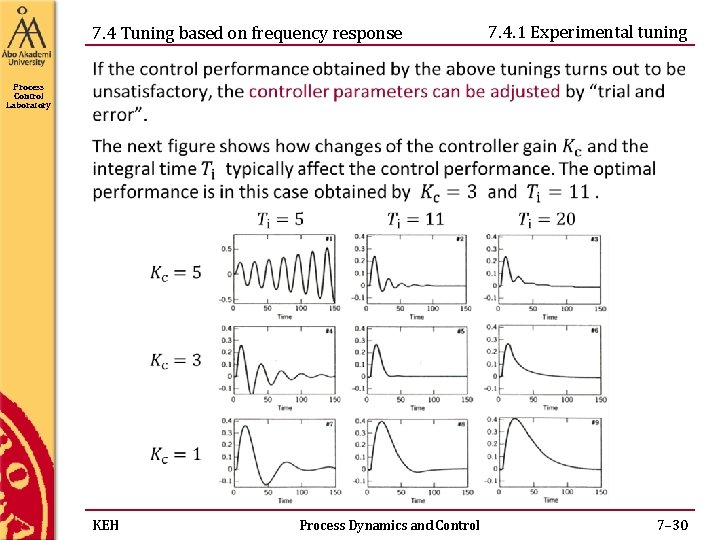
7. 4 Tuning based on frequency response 7. 4. 1 Experimental tuning Process Control Laboratory KEH Process Dynamics and Control 7– 30

7. PID Controllers Process Control Laboratory 7. 4 Tuning based on frequency response 7. 4. 2 Ziegler-Nichols’s recommendations KEH Process Dynamics and Control 7– 31

7. PID Controllers Process Control Laboratory 7. 4 Tuning based on frequency response 7. 4. 3 Åström’s and Hägglund’s correlations KEH Process Dynamics and Control 7– 32

7. PID Controllers Process Control Laboratory 7. 5 KEH Tuning based on step response Process Dynamics and Control 7– 33

7. PID Controllers 7. 5 Tuning based on step response Process Control Laboratory KEH Process Dynamics and Control 4– 34

7. PID Controllers Process Control Laboratory 7. 5 Tuning based on step response 7. 5. 1 Ziegler-Nichols’s recommendations KEH Process Dynamics and Control 7– 35

7. 5 Tuning based on step response 7. PID Controllers Process Control Laboratory 7. 5. 2 The CHR method KEH Process Dynamics and Control 7– 36

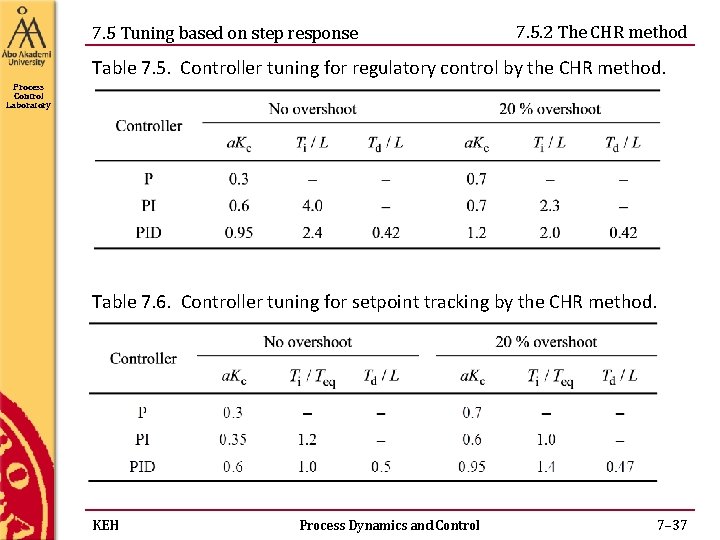
7. 5 Tuning based on step response 7. 5. 2 The CHR method Table 7. 5. Controller tuning for regulatory control by the CHR method. Process Control Laboratory Table 7. 6. Controller tuning for setpoint tracking by the CHR method. KEH Process Dynamics and Control 7– 37

7. PID Controllers Process Control Laboratory 7. 5 Tuning based on step response 7. 5. 3 Åström’s and Hägglund’s correlations KEH Process Dynamics and Control 7– 38

7. PID Controllers Process Control Laboratory 7. 6 KEH Model-based controller tuning Process Dynamics and Control 7– 39

7. PID Controllers Process Control Laboratory 7. 6 Model-based controller tuning 7. 6. 1 First-order system with a time delay KEH Process Dynamics and Control 7– 40

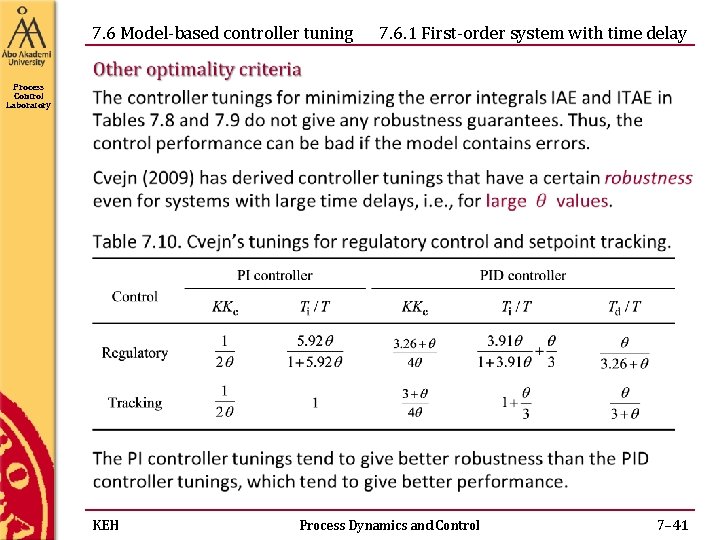
7. 6 Model-based controller tuning 7. 6. 1 First-order system with time delay Process Control Laboratory KEH Process Dynamics and Control 7– 41

7. PID Controllers Process Control Laboratory 7. 6 Model-based controller tuning 7. 6. 2 Second-order no-zero system with a time delay KEH Process Dynamics and Control 7– 42

7. 6 Model-based controller tuning 7. 6. 2 Second-order system with delay Process Control Laboratory KEH Process Dynamics and Control 7– 43

7. 6. 2 Second-order system with delay Overdamped system Process Control Laboratory KEH Process Dynamics and Control 7– 44

7. PID Controllers Process Control Laboratory 7. 7 Controller design by direct synthesis In the previous sections, equations for controller tuning have been given for first- and second-order no-zero systems. § The equations are usually the result of optimization of some criterion that is considered to imply “good control”. § However, what is “good control” varies from case to case depending on the compromise between stability and performance. § A drawback of the tuning equations is that the user cannot influence the tuning according to his/her opinion of “good control”. In this section, a method is introduced whereby § the user can influence the controller tuning in a systematic way according to his/her opinion of “good control” § more model types than in previous sections can be handled, e. g. , systems with a zero KEH Process Dynamics and Control 7– 45

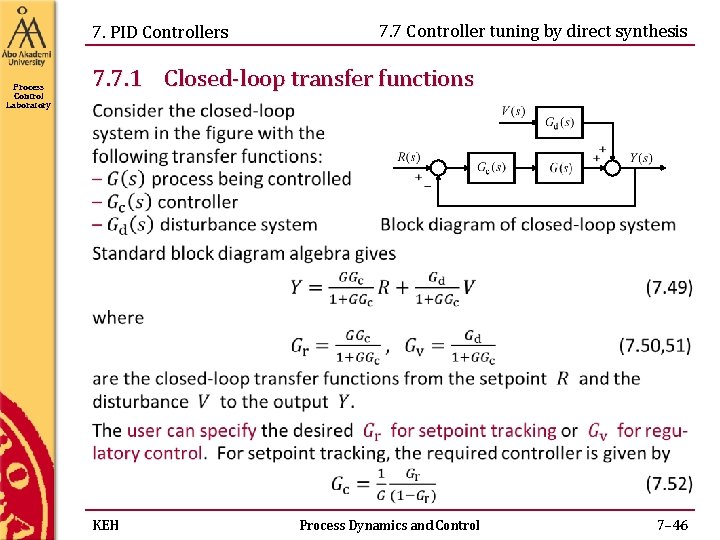
7. PID Controllers Process Control Laboratory 7. 7 Controller tuning by direct synthesis 7. 7. 1 Closed-loop transfer functions KEH Process Dynamics and Control 7– 46

7. PID Controllers Process Control Laboratory 7. 7 Controller tuning by direct synthesis 7. 7. 2 Low-order minimum-phase systems KEH Process Dynamics and Control 7– 47

7. 7 Controller tuning by direct synthesis 7. 7. 2 Low-order min-phase systems Process Control Laboratory KEH Process Dynamics and Control 7– 48

7. 7 Controller tuning by direct synthesis 7. 7. 2 Low-order min-phase systems Process Control Laboratory KEH Process Dynamics and Control 7– 49

7. PID Controllers Process Control Laboratory 7. 7 Controller tuning by direct synthesis 7. 7. 3 High-order minimum-phase systems KEH Process Dynamics and Control 7– 50

7. PID Controllers Process Control Laboratory 7. 7 Controller tuning by direct synthesis 7. 7. 4 Second-order system with RHP zero KEH Process Dynamics and Control 7– 51

7. 7 Controller tuning by direct synthesis 7. 7. 4 System with RHP zero Process Control Laboratory KEH Process Dynamics and Control 7– 52

7. 7 Controller tuning by direct synthesis 7. 7. 4 System with RHP zero Process Control Laboratory KEH Process Dynamics and Control 7– 53

7. 7. 4 Second-order system with RHP zero Closed-loop system of 2 nd order Process Control Laboratory KEH Process Dynamics and Control 7– 54

7. PID Controllers Process Control Laboratory 7. 7 Controller tuning by direct synthesis 7. 7. 5 First-order system with a time delay KEH Process Dynamics and Control 7– 55

7. 7 Controller tuning by direct synthesis 7. 7. 5 1 st order system with a delay Process Control Laboratory KEH Process Dynamics and Control 7– 56

7. 7 Controller tuning by direct synthesis 7. 7. 5 1 st order system with a delay Process Control Laboratory KEH Process Dynamics and Control 7– 57

7. PID Controllers Process Control Laboratory 7. 8 Internal model control “Internal model control” (IMC) is closely related to “direct synthesis” (DS). As in DS, a model of the system to be controlled is explicitly built into the controller, but in a different way. § An advantage with IMC is that it is easier to implement more complex control laws than regular PID controllers. For example, the controller transfer function (7. 85) can easily be implemented exactly with IMC. § Even if the controller design is based on IMC, it is often desirable to implement the controller as a regular PID controller. In such cases, the IMC approach offers better possibilities to deal with robustness issues than DS. KEH Process Dynamics and Control 7– 58

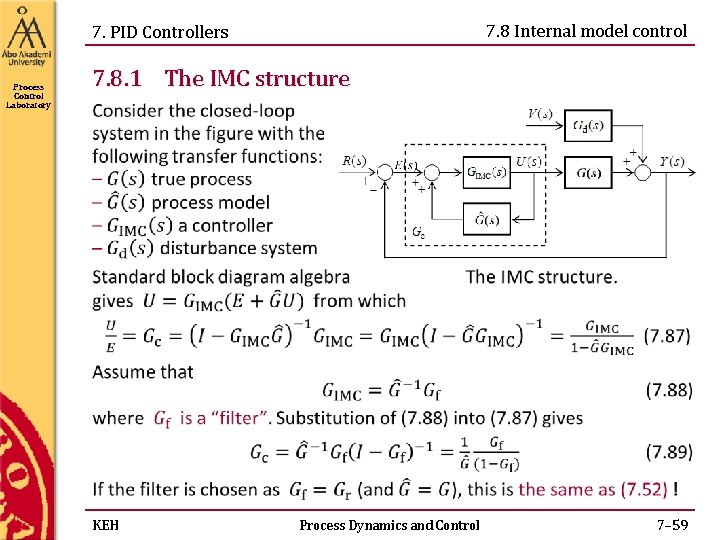
7. 8 Internal model control 7. PID Controllers Process Control Laboratory 7. 8. 1 The IMC structure KEH Process Dynamics and Control 7– 59

7. 8 Internal model control 7. PID Controllers Process Control Laboratory 7. 8. 2 Handling of time delays without approximation KEH Process Dynamics and Control 7– 60

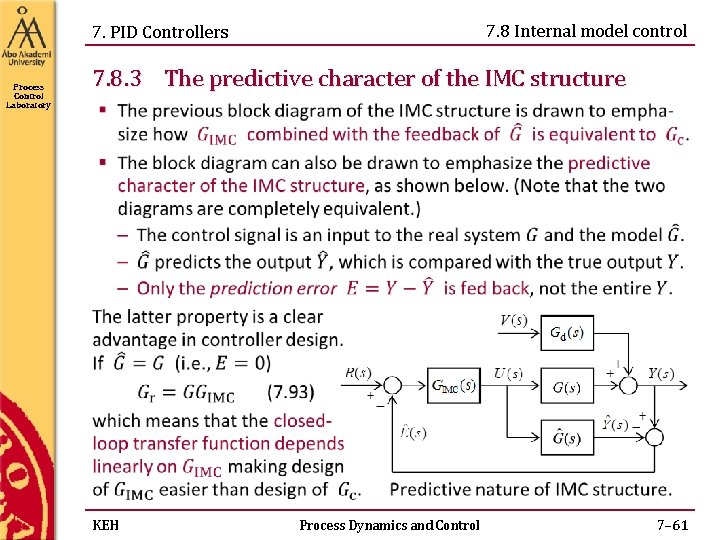
7. 8 Internal model control 7. PID Controllers Process Control Laboratory 7. 8. 3 The predictive character of the IMC structure KEH Process Dynamics and Control 7– 61

7. 8 Internal model control 7. PID Controllers Process Control Laboratory 7. 8. 4 Controller design KEH Process Dynamics and Control 7– 62

7. 8. 4 Controller design 7. 8 Internal model control Process Control Laboratory KEH Process Dynamics and Control 7– 63

7. 8 Internal model control 7. PID Controllers Process Control Laboratory 7. 8. 5 Implementation with a regular PID controller KEH Process Dynamics and Control 7– 64

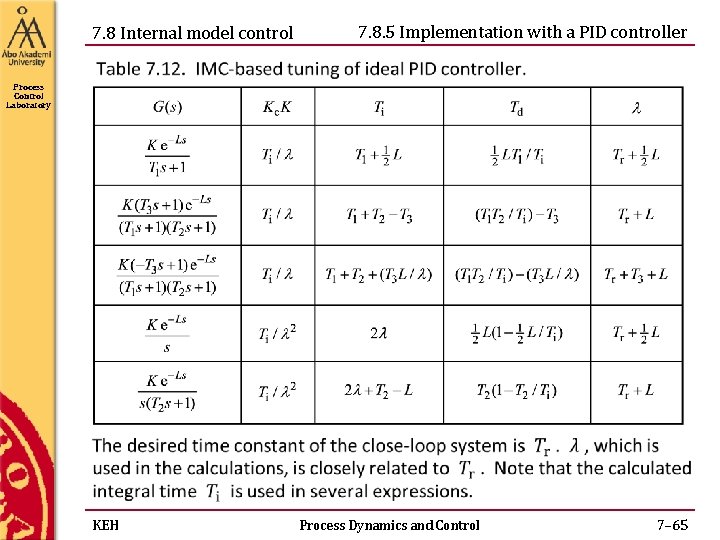
7. 8 Internal model control 7. 8. 5 Implementation with a PID controller Process Control Laboratory KEH Process Dynamics and Control 7– 65

7. PID Controllers Process Control Laboratory 7. 9 Model simplification KEH Process Dynamics and Control 7– 66

7. 9 Model simplification 7. PID Controllers Process Control Laboratory 7. 9. 1 Skogestad’s method KEH Process Dynamics and Control 7– 67

Elimination of LHP zeros 7. 9. 1 Skogestad’s method Process Control Laboratory KEH Process Dynamics and Control 7– 68

Elimination of LHP zeros 7. 9. 1 Skogestad’s method Process Control Laboratory KEH Process Dynamics and Control 7– 69

7. 9. 1 Skogestad’s method Elimination of RHP zeros and the half rule Process Control Laboratory KEH Process Dynamics and Control 7– 70

7. 9. 1 Skogestad’s method 7. 9 Model simplification Process Control Laboratory KEH Process Dynamics and Control 7– 71

Example 7. 2 7. 9. 1 Skogestad’s method Process Control Laboratory KEH Process Dynamics and Control 7– 72

7. 9 Model simplification 7. PID Controllers Process Control Laboratory 7. 9. 2 Isaksson’s and Graebe’s method KEH Process Dynamics and Control 7– 73

7. 9 Model simplification 7. 9. 2 Isakssons’s and Graebe’s method Process Control Laboratory KEH Process Dynamics and Control 7– 74

7. 9 Model simplification 7. 9. 2 Isakssons’s and Graebe’s method Process Control Laboratory KEH Process Dynamics and Control 7– 75