Process Control Charts Plot of Sample Data Over

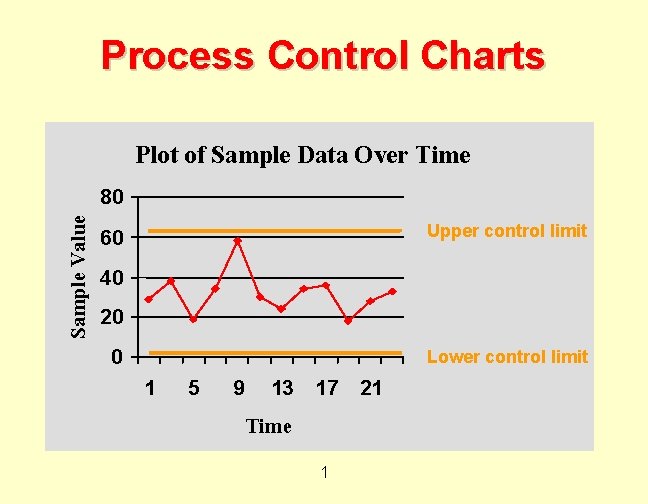
Process Control Charts Plot of Sample Data Over Time Sample Value 80 Upper control limit 60 40 20 0 Lower control limit 1 5 9 13 17 Time 1 21

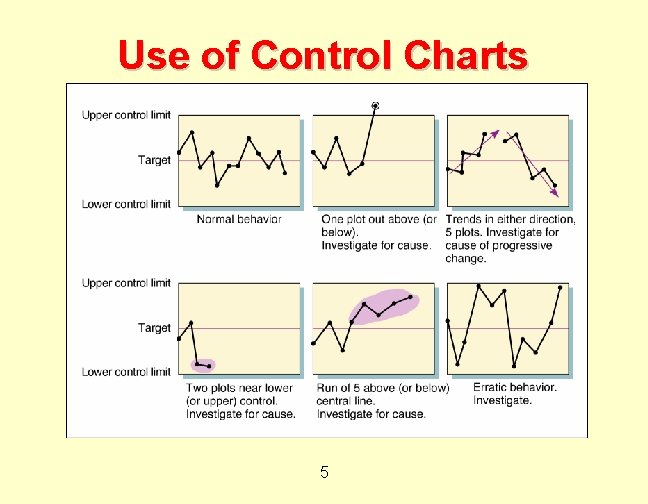
Control Charts ¨ Process is not in control if: ¨ Sample is not between upper and lower control limits. ¨ A non-random pattern is present, even when between upper and lower control limits. ¨ Based on sample being normally distributed. 2

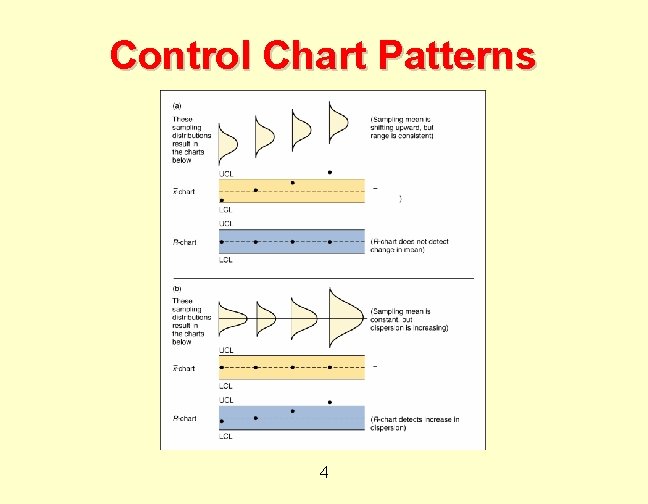
A Process in Control: ¨ Two thirds of points are near the center line ¨ A few points may be further out ¨ Points float back and forth across the centerline at random ¨ Points are balanced around the centerline ¨ There are no, or few points outside 3 limits

Control Chart Patterns 4

Use of Control Charts 5

Process capability (Ch. 11) ¨ Control charts measure what happens ¨ Involves averages of samples ¨ Specifications are what the customer wants ¨ Involves individual units ¨ Process capability: ¨ How well can a process meet customer desires? 6 ¨ Can be subjective and changing.

Estimation of population stdev. ¨ from raw data: ¨ ¨ Sigma X can be calculated directly from individuals Sigma Xbar = Sigma X / sqrt(n) ¨ ¨ Sigma X = Sbar /c 4 or Sigma X = Rbar /d 2 C 4 and d 2 are factors from the Shewhart tables. Note all of these are estimates, and probably won’t agree exactly. ¨ Estimate from sample Stdevs or Ranges: ¨ Process capability is 6 -Sigma 7

Process capability is 6 Sigma ¨ Capability Index related to Specification limits, USL and LSL: ¨ Cp = (USL-LSL) / 6 -Sigma ¨ 6 -Sigma < (USL-LSL) ; Cp>1 good situation ¨ 6 -Sigma = (USL-LSL) ; Cp =1 need center + control ¨ 6 -Sigma >(USL-LSL) ; more frequent failures even if centered and in control 8

Centering Index ¨ Even if in control and good capability, must be centered at target value to give best results. ¨ Cpk = Z(min) /3 where ¨ Zmin = smaller of Zusl = (USL-Xbar) / Sigma. X ¨ Zlsl = (Xbar-LSL) / Sigma. X ¨ ¨ Cpk = 1 if perfectly centered 9