Process Capability Analysis Measure Phase Scope of Module

Process Capability Analysis (Measure Phase)

Scope of Module • Process Variation • Process Capability – Specification, Process and Control Limits – Process Potential vs Process Performance • Short-Term vs Long-Term Process Capability • Process Capability for Non-Normal Data – Cycle-Time – Reject Rate – Defect Rate (Exponential Distribution) (Binomial Distribution) (Poisson Distribution) Process Capability Analysis 2

Process Variation is the inevitable differences among individual measurements or units produced by a process. Sources of Variation • • • within unit between units between lots between lines across time measurement error (positional variation) (unit-unit variation) (lot-lot variation) (line-line variation) (time-time variation) (repeatability & reproducibility) Process Capability Analysis 3

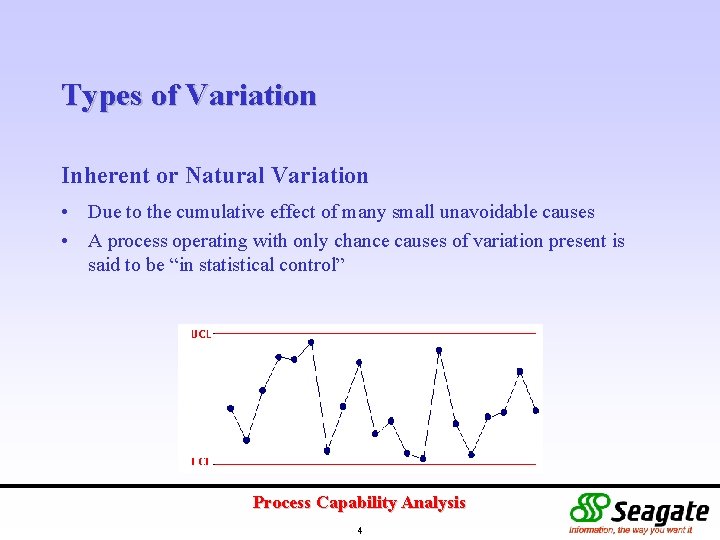
Types of Variation Inherent or Natural Variation • Due to the cumulative effect of many small unavoidable causes • A process operating with only chance causes of variation present is said to be “in statistical control” Process Capability Analysis 4

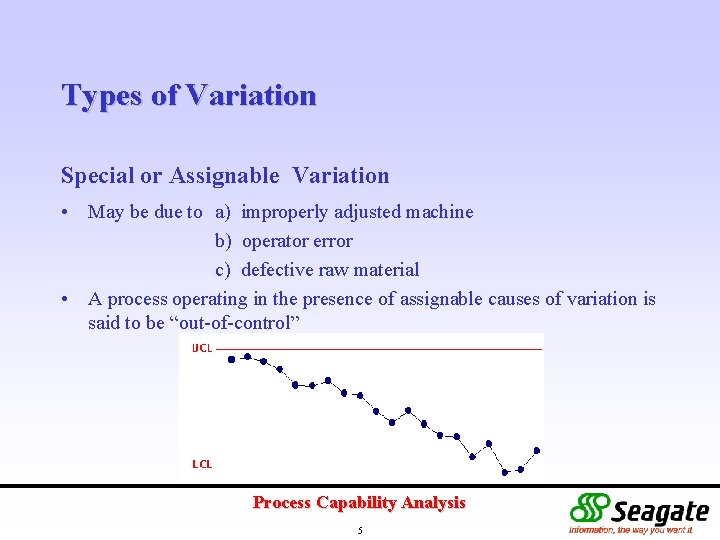
Types of Variation Special or Assignable Variation • May be due to a) improperly adjusted machine b) operator error c) defective raw material • A process operating in the presence of assignable causes of variation is said to be “out-of-control” Process Capability Analysis 5

Process Capability is the inherent reproducibility of a process’s output. It measures how well the process is currently behaving with respect to the output specifications. It refers to the uniformity of the process. Capability is often thought of in terms of the proportion of output that will be within product specification tolerances. The frequency of defectives produced may be measured in a) percentage (%) b) parts per million (ppm) c) parts per billion (ppb) Process Capability Analysis 6

Process Capability studies can • indicate the consistency of the process output • indicate the degree to which the output meets specifications • be used for comparison with another process or competitor Process Capability Analysis 7

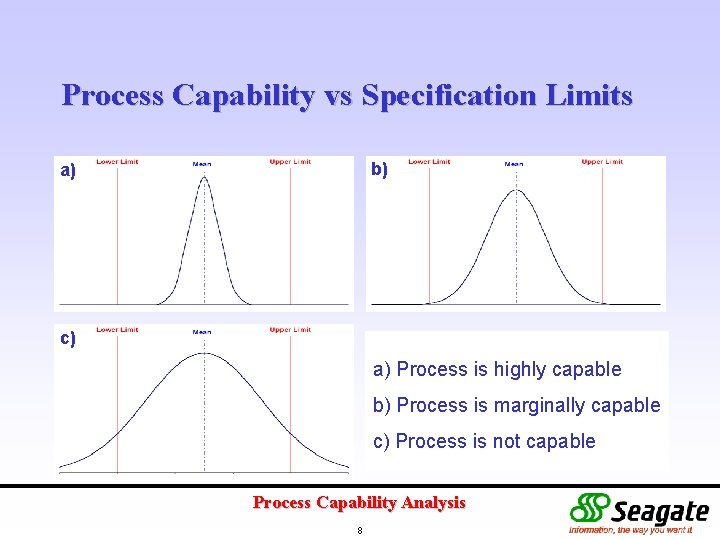
Process Capability vs Specification Limits b) a) c) a) Process is highly capable b) Process is marginally capable c) Process is not capable Process Capability Analysis 8

Three Types of Limits Specification Limits (LSL and USL) • created by design engineering in response to customer requirements to specify the tolerance for a product’s characteristic Process Limits (LPL and UPL) • measures the variation of a process • the natural 6 limits of the measured characteristic Control Limits (LCL and UCL) • measures the variation of a sample statistic (mean, variance, proportion, etc) Process Capability Analysis 9

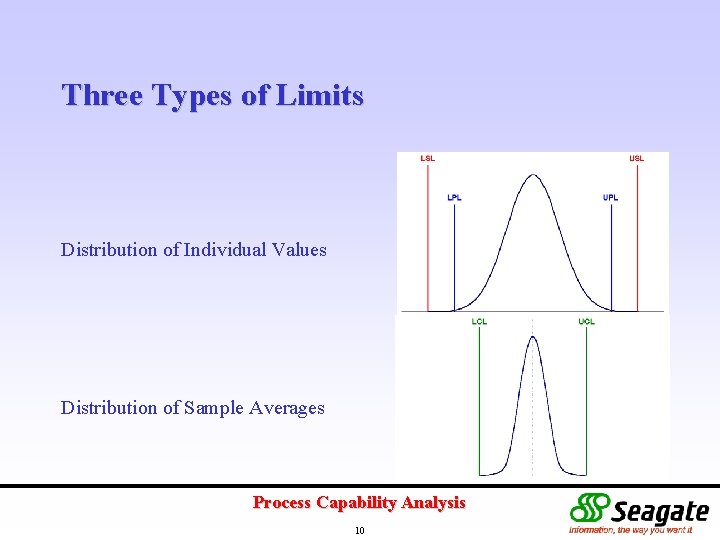
Three Types of Limits Distribution of Individual Values Distribution of Sample Averages Process Capability Analysis 10

Process Capability Indices Two measures of process capability • Process Potential – Cp • Process Performance – Cpu – Cpl – Cpk Process Capability Analysis 11

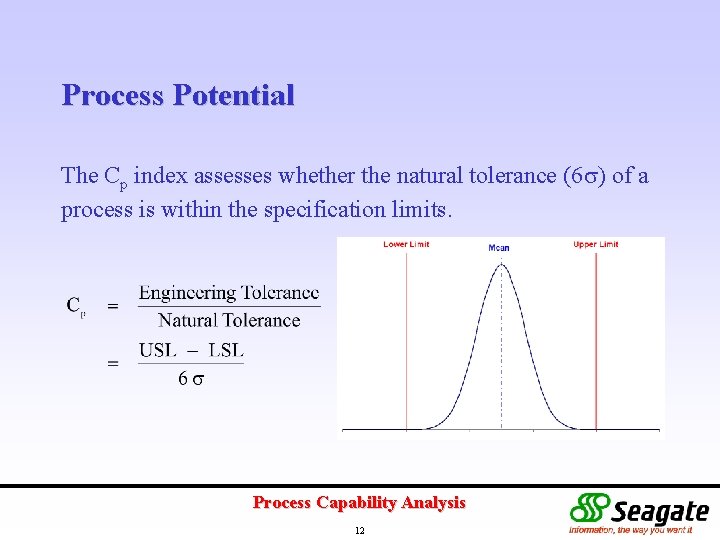
Process Potential The Cp index assesses whether the natural tolerance (6 ) of a process is within the specification limits. Process Capability Analysis 12

Process Potential A Cp of 1. 0 indicates that a process is judged to be “capable”, i. e. if the process is centered within its engineering tolerance, 0. 27% of parts produced will be beyond specification limits. Cp 1. 00 1. 33 1. 50 2. 00 Reject Rate 0. 270 % 0. 007 % 6. 8 ppm 2. 0 ppb Process Capability Analysis 13

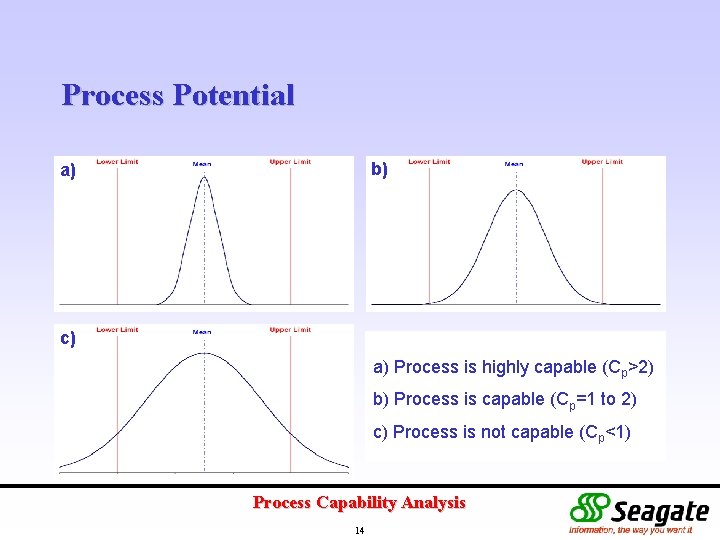
Process Potential b) a) c) a) Process is highly capable (Cp>2) b) Process is capable (Cp=1 to 2) c) Process is not capable (Cp<1) Process Capability Analysis 14

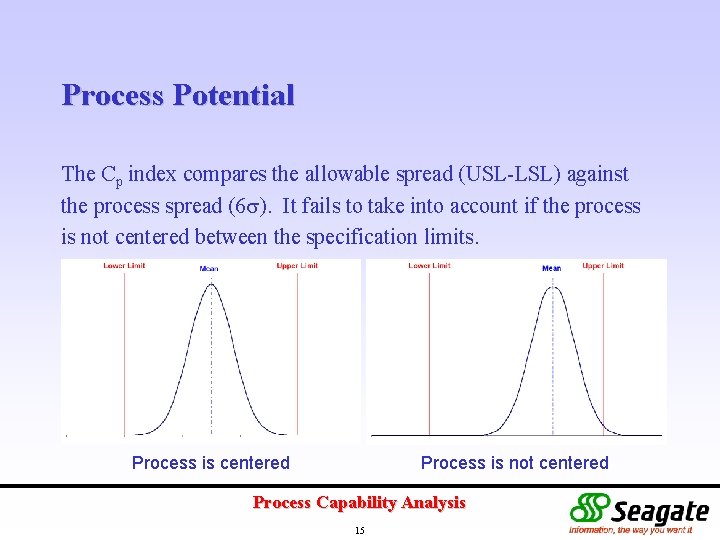
Process Potential The Cp index compares the allowable spread (USL-LSL) against the process spread (6 ). It fails to take into account if the process is not centered between the specification limits. Process is centered Process is not centered Process Capability Analysis 15

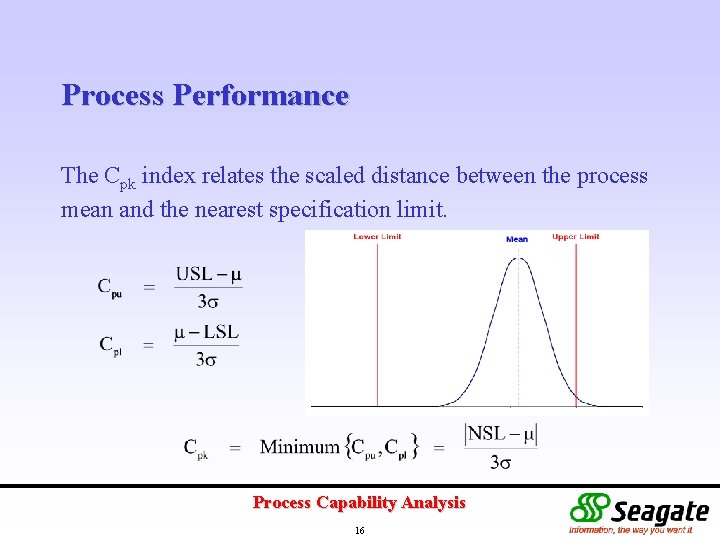
Process Performance The Cpk index relates the scaled distance between the process mean and the nearest specification limit. Process Capability Analysis 16

Process Performance Cpk Reject Rate 1. 0 1. 1 1. 2 1. 3 1. 4 1. 5 1. 6 1. 7 1. 8 1. 9 2. 0 0. 13 – 0. 27 % 0. 05 – 0. 10 % 0. 02 – 0. 03 % 48. 1 – 96. 2 ppm 13. 4 – 26. 7 ppm 3. 4 – 6. 8 ppm 794 – 1589 ppb 170 – 340 ppb 33 – 67 ppb 6 – 12 ppb 1– 2 ppb Process Capability Analysis 17

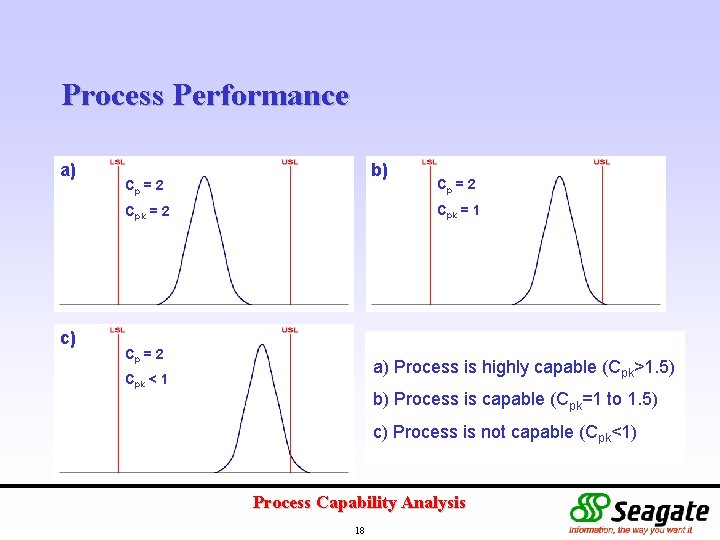
Process Performance a) b) Cp = 2 Cpk = 1 Cpk = 2 c) Cp = 2 a) Process is highly capable (Cpk>1. 5) Cpk < 1 b) Process is capable (Cpk=1 to 1. 5) c) Process is not capable (Cpk<1) Process Capability Analysis 18

Example 1 Specification Limits : 4 to 16 g Machine (a) (b) (c) (d) Std Dev 4 2 2 1 Mean 10 10 7 13 Determine the corresponding Cp and Cpk for each machine. Process Capability Analysis 19

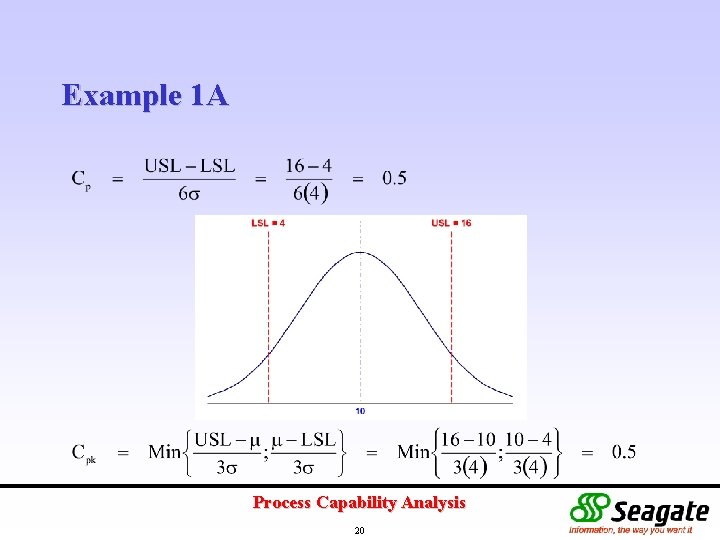
Example 1 A Process Capability Analysis 20

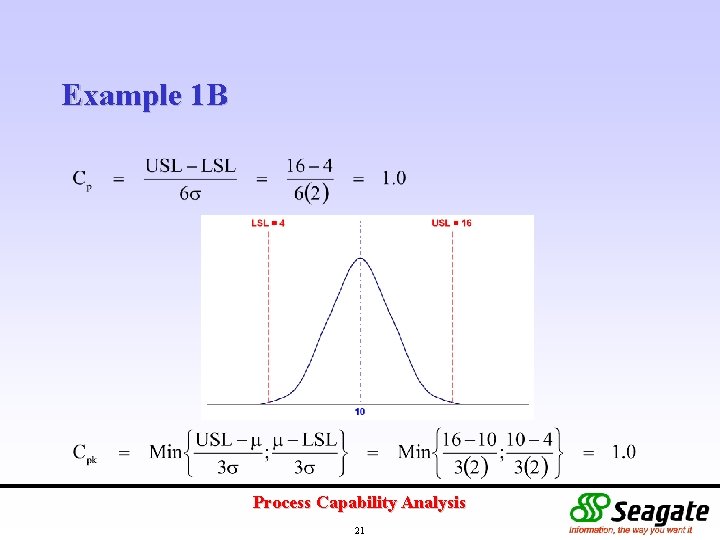
Example 1 B Process Capability Analysis 21

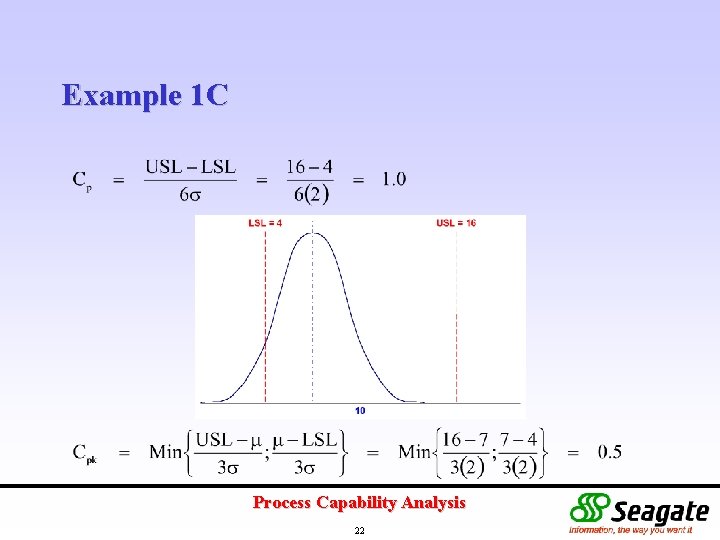
Example 1 C Process Capability Analysis 22

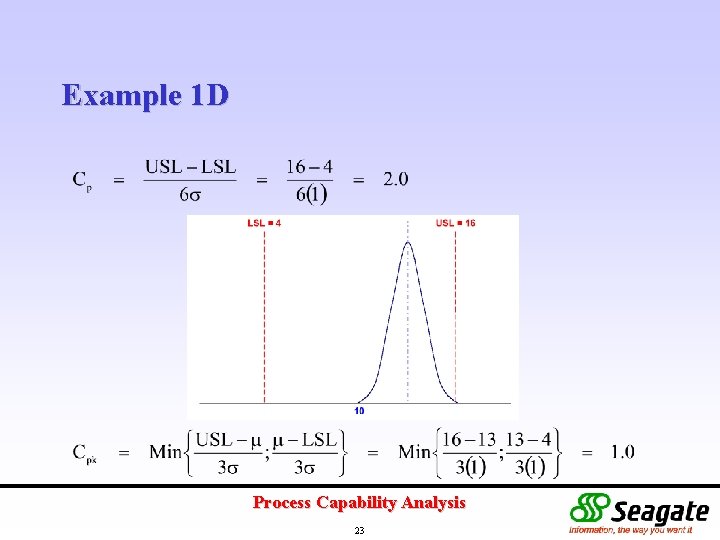
Example 1 D Process Capability Analysis 23

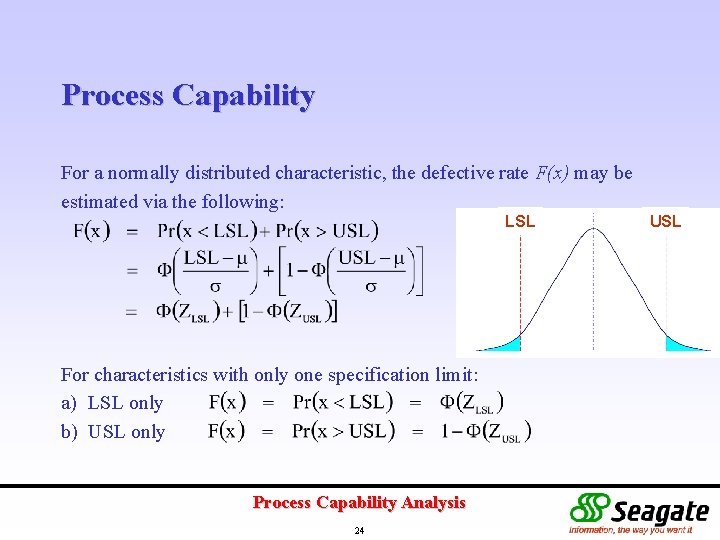
Process Capability For a normally distributed characteristic, the defective rate F(x) may be estimated via the following: LSL For characteristics with only one specification limit: a) LSL only b) USL only Process Capability Analysis 24 USL

Example 2 Specification Limits : 4 to 16 g Machine (a) (b) (c) (d) Std Dev 4 2 2 1 Mean 10 10 7 13 Determine the defective rate for each machine. Process Capability Analysis 25

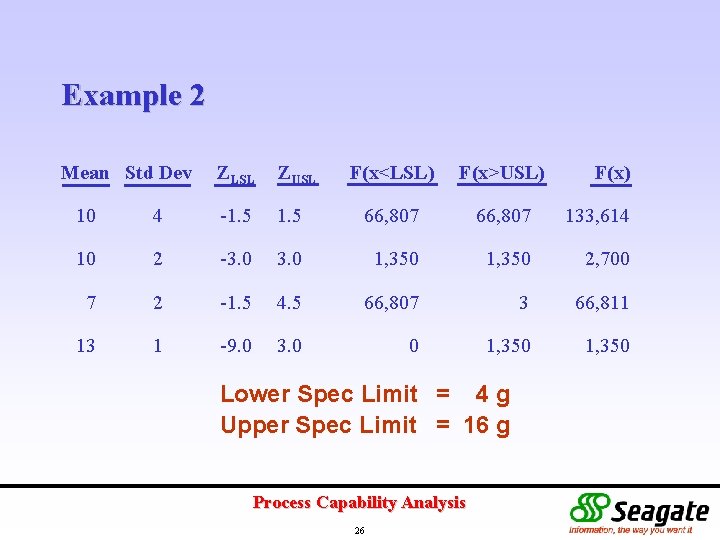
Example 2 Mean Std Dev ZLSL ZUSL F(x<LSL) F(x>USL) F(x) 10 4 -1. 5 66, 807 133, 614 10 2 -3. 0 1, 350 2, 700 7 2 -1. 5 4. 5 66, 807 3 66, 811 13 1 -9. 0 3. 0 0 1, 350 Lower Spec Limit = 4 g Upper Spec Limit = 16 g Process Capability Analysis 26

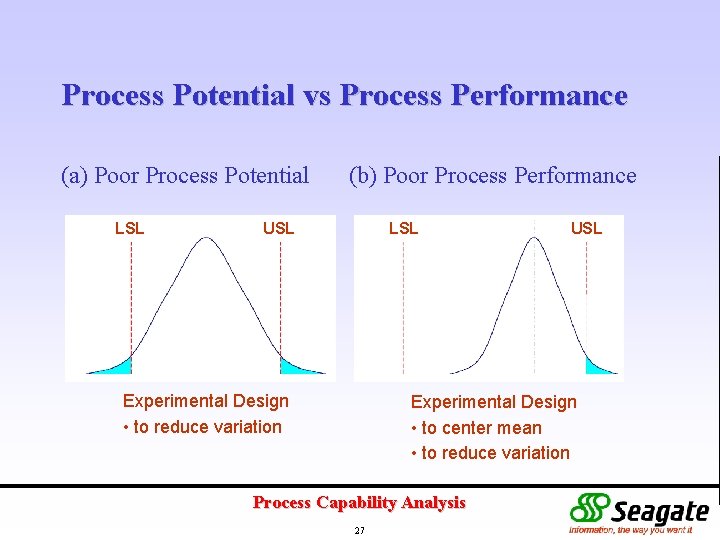
Process Potential vs Process Performance (a) Poor Process Potential LSL (b) Poor Process Performance USL LSL Experimental Design • to reduce variation USL Experimental Design • to center mean • to reduce variation Process Capability Analysis 27

Process Potential vs Process Performance Cpk 1. 0 1. 2 1. 4 1. 0 Process Potential Index (Cp) 1. 2 1. 4 1. 6 1. 8 2. 0 2, 699. 9 1, 363. 3 1, 350. 0 318. 3 159. 9 159. 1 26. 7 13. 4 1. 6 0. 8 0. 1 0. 0 1. 6 1. 8 2. 0 0. 0 Defective Rate (measured in dppm) is dependent on the actual combination of Cp and Cpk. . Process Capability Analysis 28

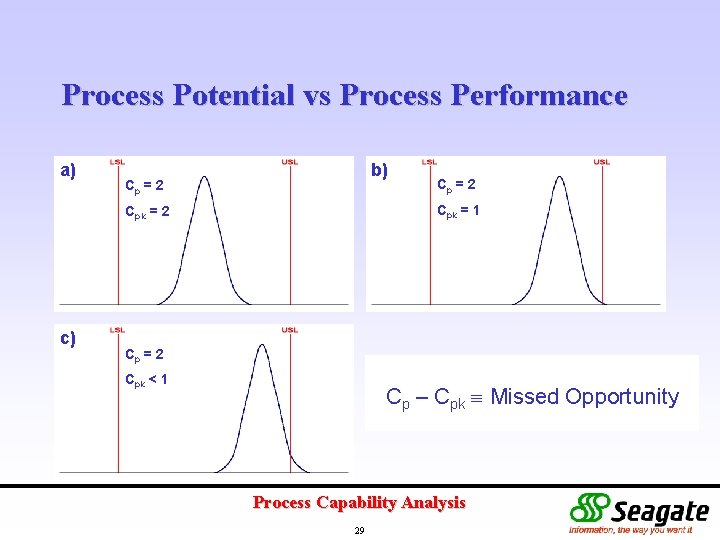
Process Potential vs Process Performance a) b) Cp = 2 Cpk = 1 Cpk = 2 c) Cp = 2 Cpk < 1 Cp – Cpk Missed Opportunity Process Capability Analysis 29

Alternative Process Performance Index Process capability statistics measure process variation relative to specification limits. The Cp statistic compares the engineering tolerance against the process’s natural variation. The Cpk statistic takes into account the location of the process relative to the midpoint between specifications. If the process target is not centered between specifications, the Cpm statistic is preferred. Process Capability Analysis 30

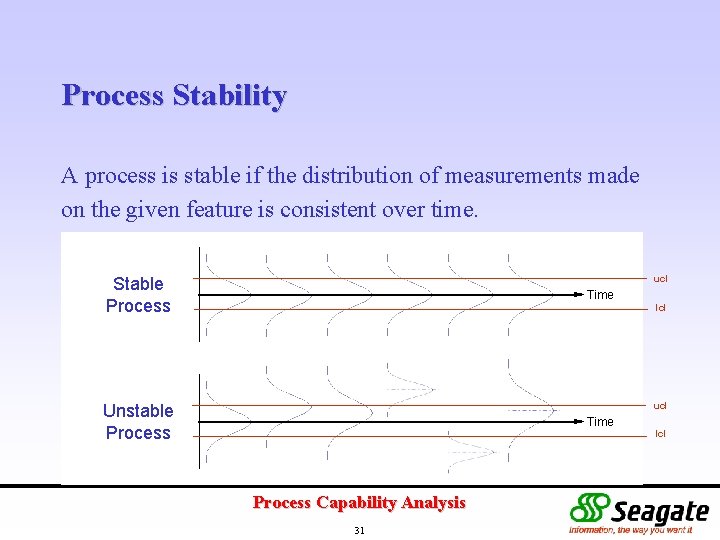
Process Stability A process is stable if the distribution of measurements made on the given feature is consistent over time. ucl Stable Process Time lcl ucl Unstable Process Time Process Capability Analysis 31 lcl

Within vs Overall Capability Within Capability (previously called short-term capability) shows the inherent variability of a machine/process operating within a brief period of time. Overall Capability (previously called long-term capability) shows the variability of a machine/process operating over a period of time. It includes sources of variation in addition to the short-term variability. Process Capability Analysis 32

Within vs Overall Capability Within Overall Sample Size 30 – 50 units 100 units Number of Lots single lot several lots Period of Time hours or days weeks or months Number of Operators single operator different operators Process Potential Cp Pp Process Performance Cpk Process Capability Analysis 33

Within vs Overall Capability Within Capability Overall Capability The key difference between the two sets of indices lies in the estimates for Within and Overall. Process Capability Analysis 34

Estimating Within and Overall Consider the following observations from a Control Chart: S/N X 1 X 2 … Xk Mean 1 2 : m x 1, 1 x 1, 2 : x 1, m x 2, 1 x 2, 2 : x 2, m … … xk, 1 xk, 2 : xk, m – X 1 – X 2 : – X m … The overall variation Overall is estimated by Process Capability Analysis 35 Range Std Dev R 1 R 2 : Rm S 1 S 2 : Sm

Estimating Within and Overall The within variation Within may be estimated by one of the following: (a) R-bar Method where d 2 is a Shewhart constant = (k) where c 4 is a Shewhart constant = (k) (b) S-bar Method (c) Pooled Standard Deviation Method In Mini. Tab, the Pooled Standard Deviation is the default method. Process Capability Analysis 36

Estimating Within and Overall In cases where there is only 1 observation per sub-group (i. e. k=1), the Moving Range Method is used, where. The within variation Within is then estimated using either a) the Average Moving Range : b) the Median Moving Range : Process Capability Analysis 37

Example 3 The length of a camshaft for an automobile engine is specified at 600 ± 2 mm. Control of the length of the camshaft is critical to avoid scrap/rework. The camshaft is provided by an external supplier. Assess the process capability for this supplier. The data is available in Process Capability Analysis. MTW. Process Capability Analysis 38

Example 3 Stat Quality Tools Capability Analysis (Normal) Process Capability Analysis 39

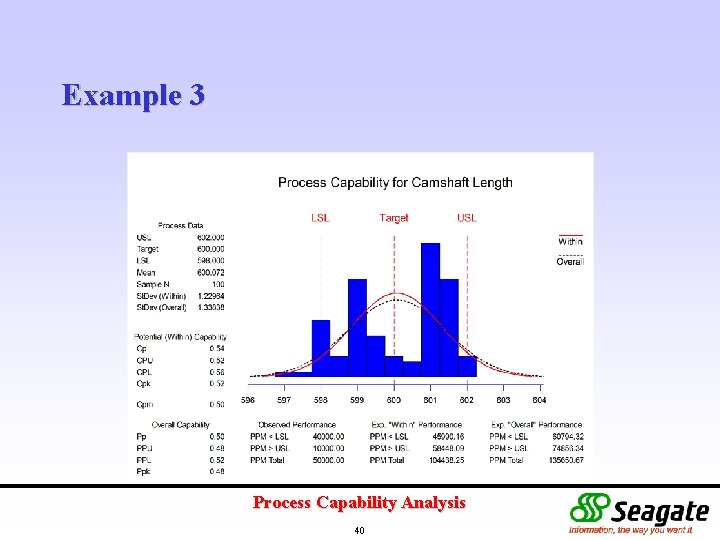
Example 3 Process Capability Analysis 40

Example 3 A Histogram of camshaft length suggests mixed populations. Further investigation revealed that there are two suppliers for the camshaft. Data was collected over camshafts from both sources. Are the two suppliers similar in performance? If not, what are your recommendations? Process Capability Analysis 41

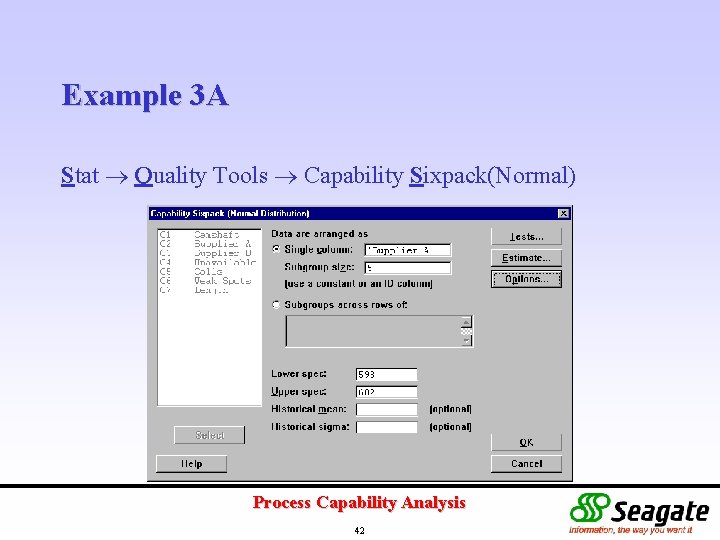
Example 3 A Stat Quality Tools Capability Sixpack(Normal) Process Capability Analysis 42

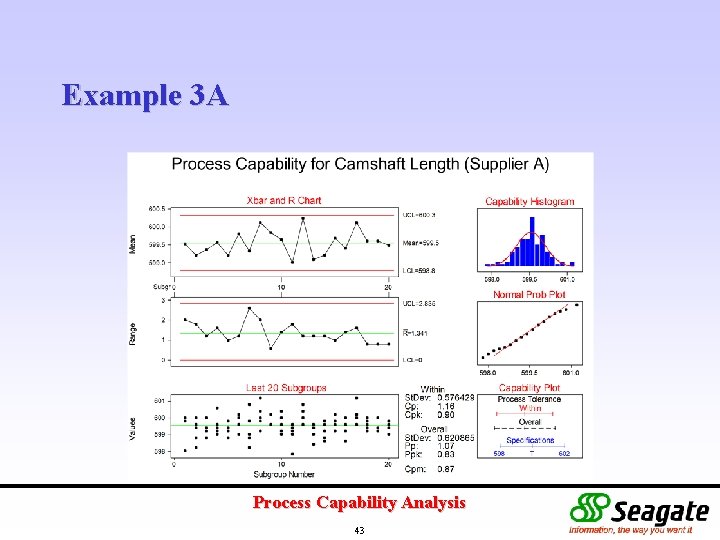
Example 3 A Process Capability Analysis 43

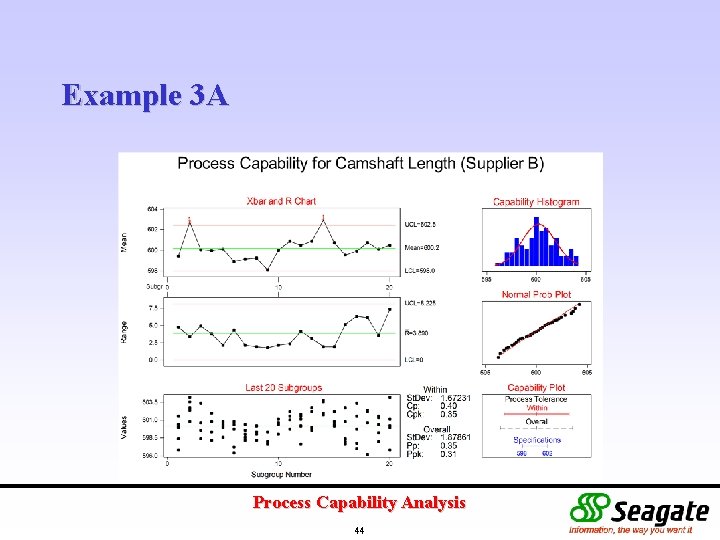
Example 3 A Process Capability Analysis 44

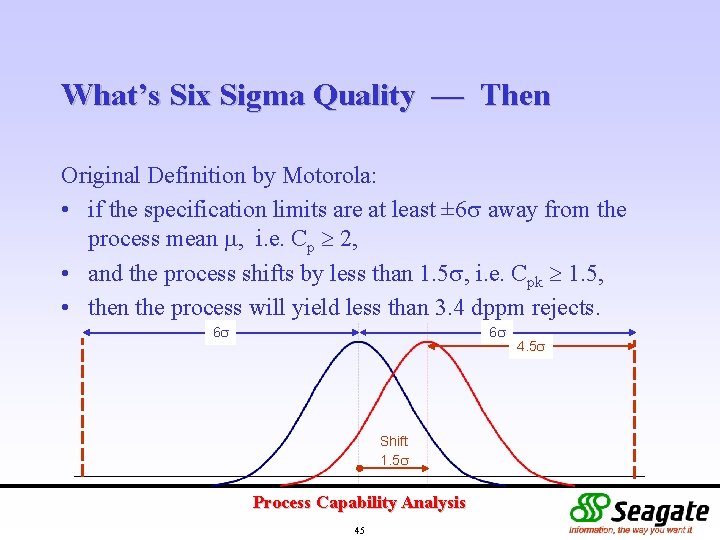
What’s Six Sigma Quality — Then Original Definition by Motorola: • if the specification limits are at least ± 6 away from the process mean , i. e. Cp 2, • and the process shifts by less than 1. 5 , i. e. Cpk 1. 5, • then the process will yield less than 3. 4 dppm rejects. 6 6 Shift 1. 5 Process Capability Analysis 45 4. 5

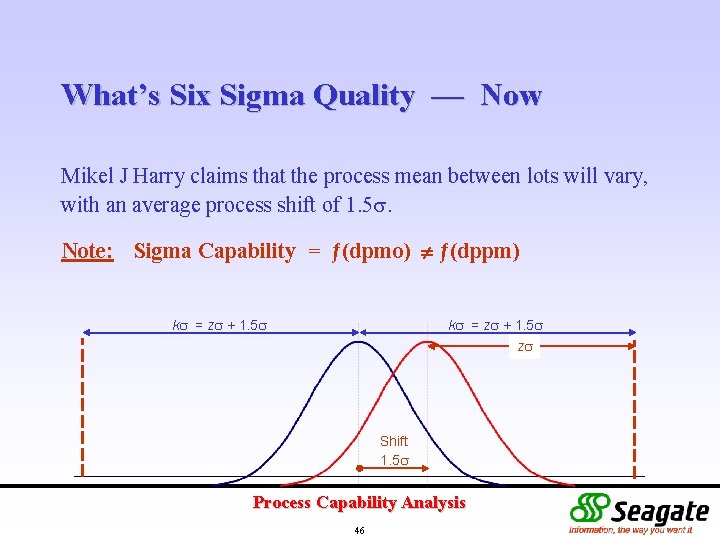
What’s Six Sigma Quality — Now Mikel J Harry claims that the process mean between lots will vary, with an average process shift of 1. 5. Note: Sigma Capability = ƒ(dpmo) ƒ(dppm) k = z + 1. 5 z k = z + 1. 5 Shift 1. 5 Process Capability Analysis 46

Process Capability for Non-Normal Data Not every measured characteristic is normally distributed. Characteristic Cycle Time Reject Rate Defect Rate Distribution Exponential Binomial Poisson Process Capability Analysis 47

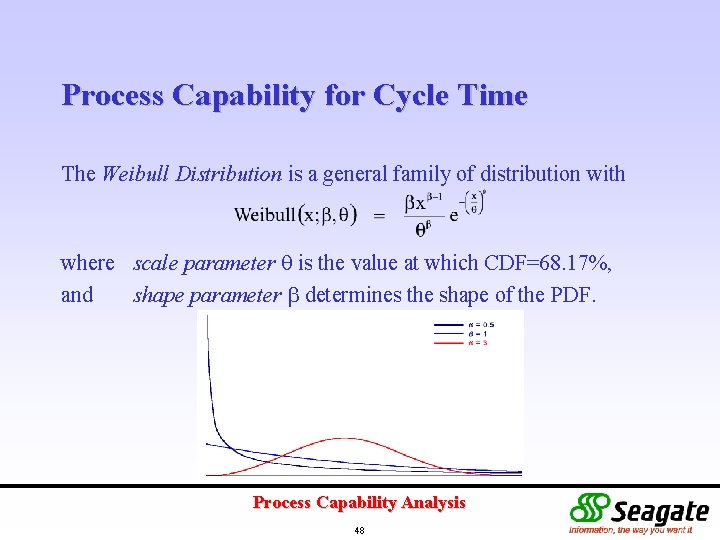
Process Capability for Cycle Time The Weibull Distribution is a general family of distribution with where scale parameter is the value at which CDF=68. 17%, and shape parameter determines the shape of the PDF. Process Capability Analysis 48

Process Capability for Cycle Time At =1, the Weibull Distribution is reduced to Weibull (x; =1, ) For an Exponential Distribution, Exponential (x; ) The Exponential Distribution is thus a Weibull Distribution with =1. Process Capability Analysis 49

Example 4 A customer service manager wants to determine the process capability for his department. A primary performance index is the time taken to close a customer complaint. The goal for this index is to close a complaint within one calendar week. Performance over the last 400 complaints was reviewed. Process Capability Analysis 50

Example 4 Stat Quality Tools Capability Analysis (Weibull) Process Capability Analysis 51

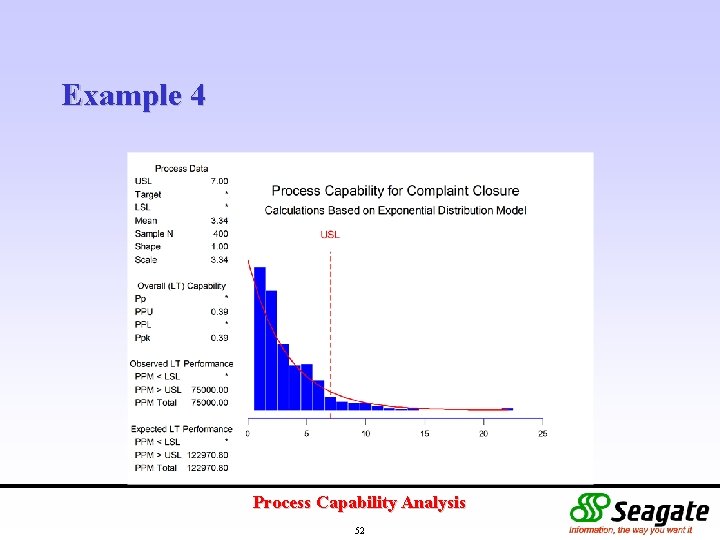
Example 4 Process Capability Analysis 52

Example 4 A Stat Quality Tools Capability Sixpack (Weibull) Process Capability Analysis 53

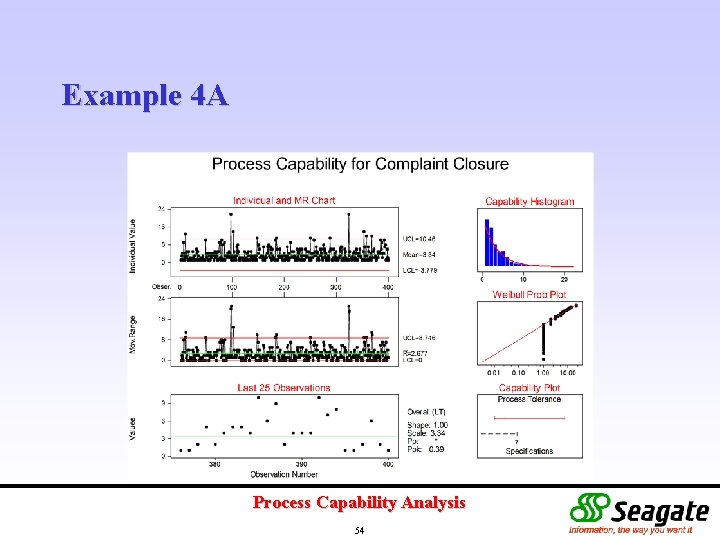
Example 4 A Process Capability Analysis 54

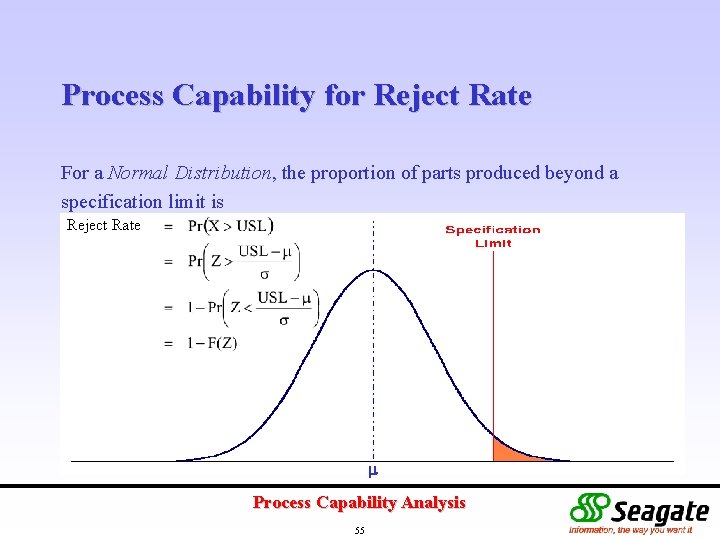
Process Capability for Reject Rate For a Normal Distribution, the proportion of parts produced beyond a specification limit is Reject Rate Process Capability Analysis 55

Process Capability for Reject Rate Thus, for every reject rate there is an accompanying Z-Score, where Recall that Hence Process Capability Analysis 56

Process Capability for Reject Rate Estimation of Ppk for Reject Rate • Determine the long-term reject rate (p) • Determine the inverse cumulative probability for p, using Calc Probability Distribution Normal • Z-Score is the magnitude of the returned value • Ppk is one-third of the Z-Score Process Capability Analysis 57

Example 5 A sales manager plans to assess the process capability of his telephone sales department’s handling of incoming calls. The following data was collected over a period of 20 days: • number of incoming calls per day • number of unanswered calls per days Process Capability Analysis 58

Example 5 Stat Quality Tools Capability Analysis (Binomial) Process Capability Analysis 59

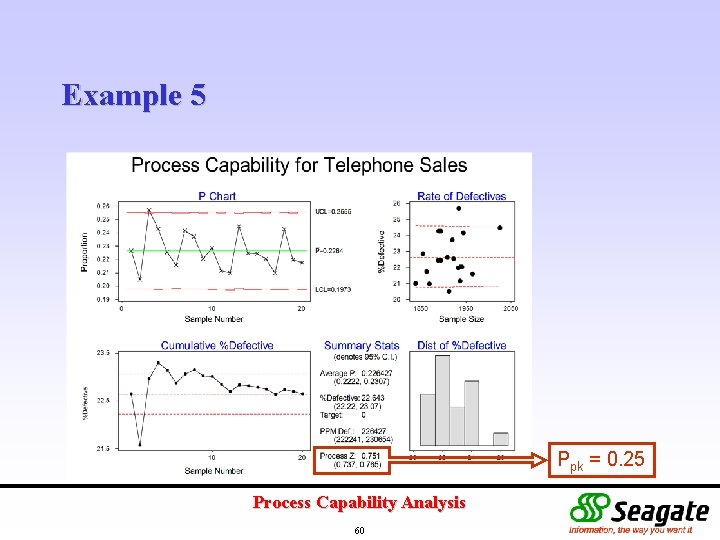
Example 5 Ppk = 0. 25 Process Capability Analysis 60

Process Capability for Defect Rate Other applications, approximating a Poisson Distribution : • error rates • particle count • chemical concentration Process Capability Analysis 61

Process Capability for Defect Rate Estimation of Ytp for Defect Rate • Define size of an inspection unit • Determine the long-term defects per unit (DPU) DPU = Total Defects Total Units • Determine throughput yield (Ytp) Ytp = exp{–DPU} Process Capability Analysis 62

Process Capability for Defect Rate Estimation of Sigma-Capability for Defect Rate • Determine the opportunities per unit • Determine the long-term defects per opportunity (d) d = defects per unit opportunities per unit • Determine the inverse cumulative probability for d, using Calc Probability Distribution Normal • Z-Score is the magnitude of the returned value • Sigma-Capability = Z-Score + 1. 5 Process Capability Analysis 63

Example 6 The process manager for a wire manufacturer is concerned about the effectiveness of the wire insulation process. Random lengths of electrical wiring are taken and tested for weak spots in their insulation by means of a test voltage. The number of weak spots and the length of each piece of wire are recorded. Process Capability Analysis 64

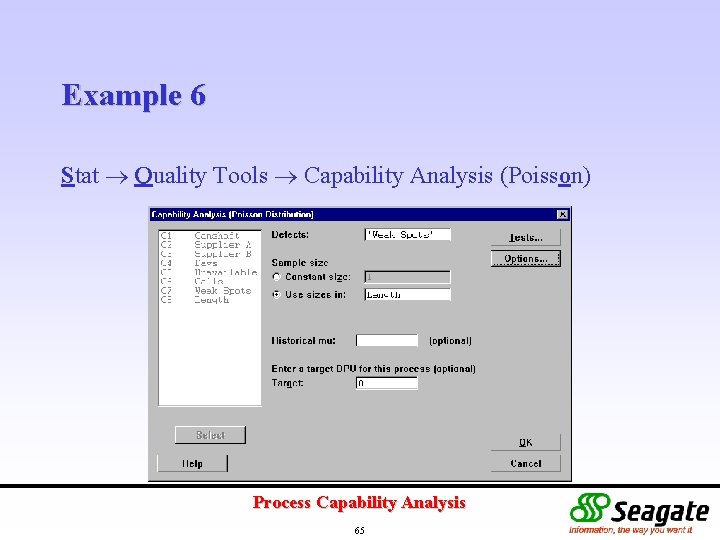
Example 6 Stat Quality Tools Capability Analysis (Poisson) Process Capability Analysis 65

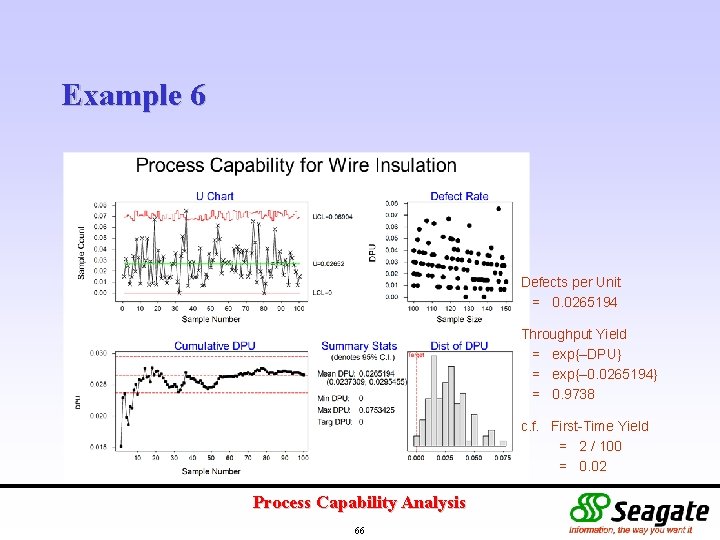
Example 6 Defects per Unit = 0. 0265194 Throughput Yield = exp{–DPU} = exp{– 0. 0265194} = 0. 9738 c. f. First-Time Yield = 2 / 100 = 0. 02 Process Capability Analysis 66

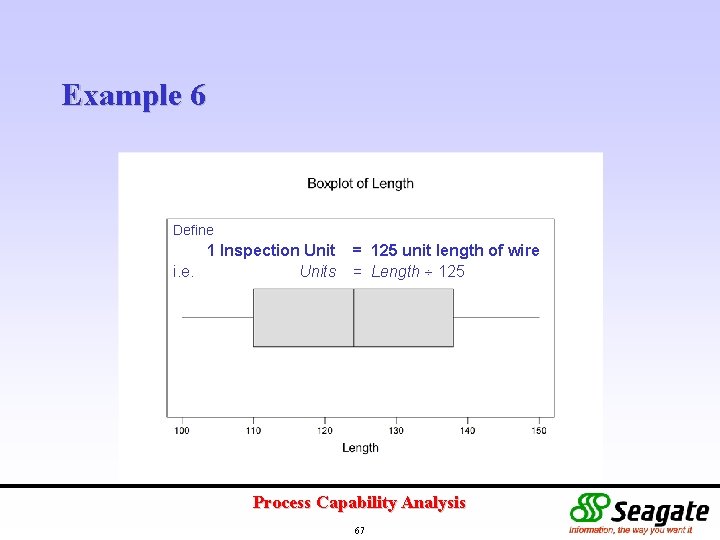
Example 6 Define 1 Inspection Unit i. e. Units = 125 unit length of wire = Length 125 Process Capability Analysis 67

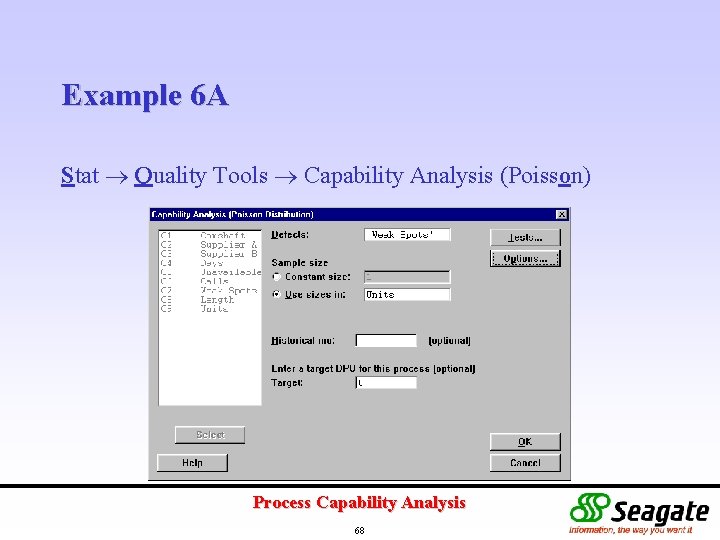
Example 6 A Stat Quality Tools Capability Analysis (Poisson) Process Capability Analysis 68

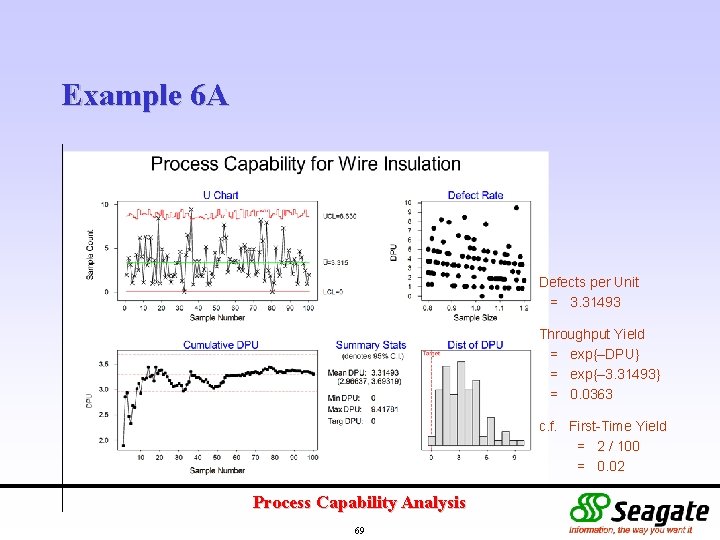
Example 6 A Defects per Unit = 3. 31493 Throughput Yield = exp{–DPU} = exp{– 3. 31493} = 0. 0363 c. f. First-Time Yield = 2 / 100 = 0. 02 Process Capability Analysis 69

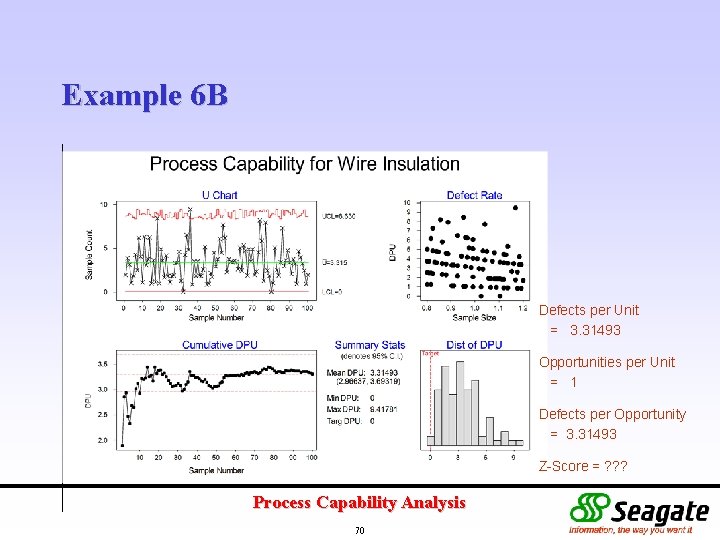
Example 6 B Defects per Unit = 3. 31493 Opportunities per Unit = 1 Defects per Opportunity = 3. 31493 Z-Score = ? ? ? Process Capability Analysis 70

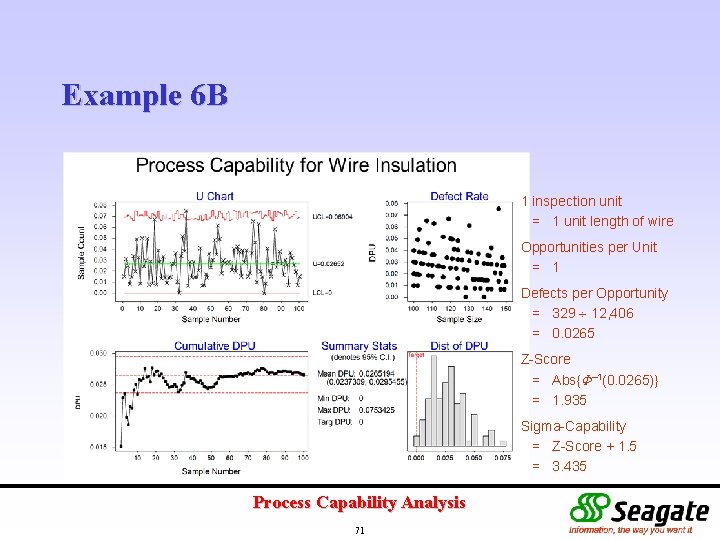
Example 6 B 1 inspection unit = 1 unit length of wire Opportunities per Unit = 1 Defects per Opportunity = 329 12, 406 = 0. 0265 Z-Score = Abs{ – 1(0. 0265)} = 1. 935 Sigma-Capability = Z-Score + 1. 5 = 3. 435 Process Capability Analysis 71

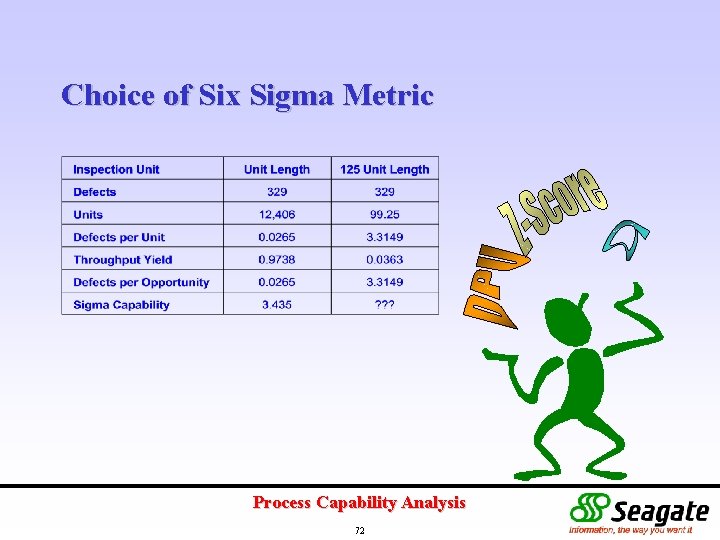
Choice of Six Sigma Metric Process Capability Analysis 72