Procedural Texture Synthesis Patterns from Algorithms Procedural Synthesis

Procedural Texture Synthesis Patterns from Algorithms

Procedural Synthesis • The basic problem: Worlds are big. – To create models and textures for even fairly small worlds takes ages, if you do it by hand. • Idea: write down the rules of the world, and a program can create the content. • Philosophy of algorithmic synthesis: proceduralism.

[World of Warcraft, 2004 -2010]

[Oblivion, 2006]

Procedural Texture • Simplest form: function evaluation – T(x, y) = ? • Instead of accessing texture memory, directly compute the texture value • Pro: saves memory, bus • Con: need the algorithm – and, need a shader, but normally would have that anyway

Proceduralism vs Reuse • Reuse: simple repetition of models, textures • Proceduralism: new models, textures by rerunning algorithm with different inputs – trivially, different random seed

Sophisticated reuse • Use small pieces – reuse not so obvious – "Lego blocks" • Modular design: blocks are big (e. g. , section of tunnel) – might be OK in industrial fiction • "divine corpse" for monsters, architecture • Penrose tiles, Wang tiles for texture, terrain – Reuse with rotation, less apparent – city setting: regular layout

Texture Synthesis Primitives • Building blocks for textures: – noise – Perlin noise – Voronoi cells – many others • Rosalind Picard: "a society of models"

Texture Basis • "basis functions" for texture • primitive functions used as foundation for specific functions aimed at specific effects • Perlin noise: "the function that launched a thousand textures"

Noise • Simple and straightforward: – N(x, y) = random(range) • Introduces much-needed randomness • But: – lacks coherence – cannot be sensibly subsampled, supersampled

Perlin Noise • Ken Perlin, 1985 • random 4 -vector at each node on an integer lattice: {a, b, c, d}[x][y][z] Noise[x][y][z] = d[x][y][z] if x, y, z are integers otherwise, interpolate ax+d, by+d, cz+d using spline 2 t^3 – 3 t^2

DNoise • Noise() is a scalar • Can get vector-valued function (for bump mapping, say) by taking the gradient of Noise()

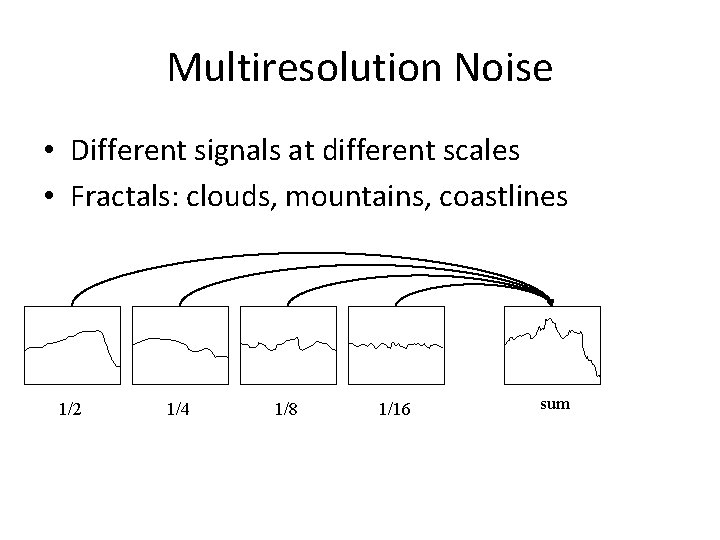
Multiresolution Noise • Different signals at different scales • Fractals: clouds, mountains, coastlines 1/2 1/4 1/8 1/16 sum

Multiresolution Noise • aka "turbulence" • FNoise(x, y, z) = Σ((2 -i)*Noise(x*2 i…)) • Extremely common formulation – so common that many mistake it for the basic noise primitive

Attributes of Perlin Noise • • Reproducible Coherent Continuous in first derivative Arbitrary resolution • Used as input to other functions

Perlin Marble • texture = cos(x + a*Noise(x, y)) – or, texture = cos(x + a*Turb(x, y)) • properly renormalized, of course! • purple/white color map • value of parameter a says how noisy the marble is

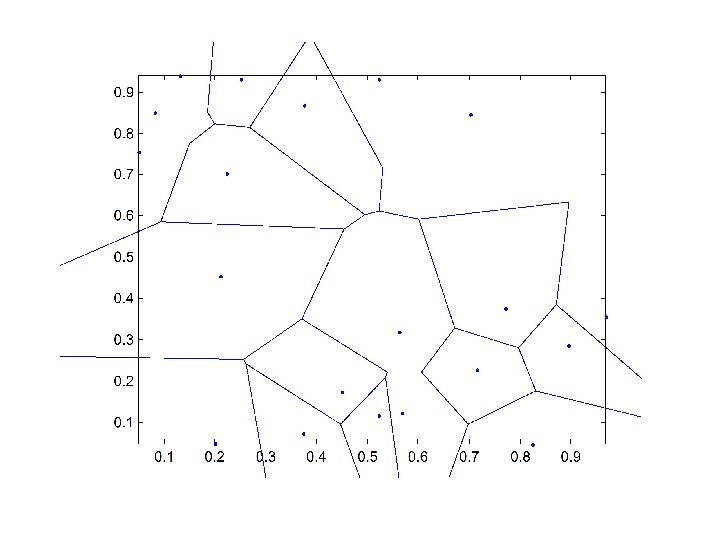
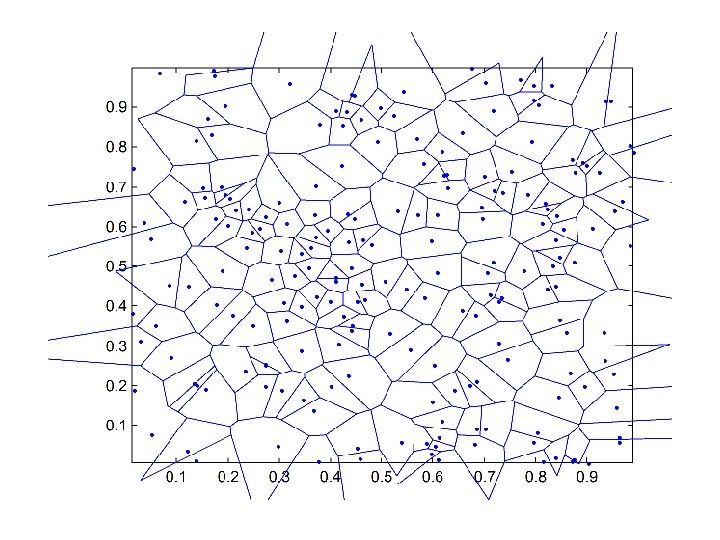
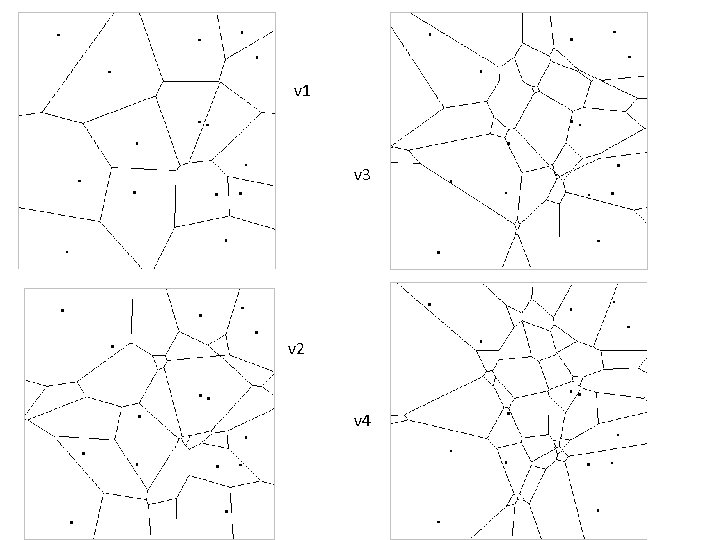
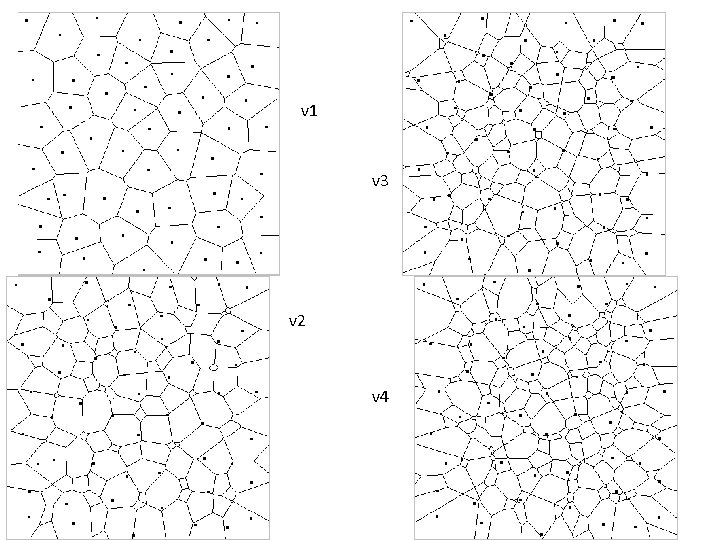
Cellular Texture • “Worley texture”, Worley 1996 • Based on the Voronoi diagram: partition of plane according to nearest point • Use nth-order distances (closest, second closest…) as basis

v 1 v 3 v 2 v 4

v 1 v 3 v 2 v 4

Combining distances • Having normalized distances, can combine – say D 1, D 2, D 3, D 4 • Take (say) 2*D 1 – D 3 • Linear transformation given by 4 coefficients: – C 1 D 1 + C 2 D 2 + C 3 D 3 + C 4 D 4 • manipulate coefficients to obtain effects