Problems of the Day 1 Find the slope

Problems of the Day 1. ) Find the slope of the line that contains (– 9, 8) and (5, – 4). 2. )Find the value of r so that the line through (10, -3) and (r, 6) has a slope of -3/2.

Chapter 5. 2 Slope and Direct Variation

A recipe for paella calls for 1 cup of rice to make 5 servings. In other words, a chef needs 1 cup of rice for every 5 servings. The equation y = 5 x describes this relationship. In this relationship, the number of servings varies directly with the number of cups of rice.

A direct variation is a special type of linear relationship that can be written in the form y = kx, where k is a nonzero constant called the constant of variation.

Ex. 1 Name the constant variation for the equation. Then find the slope of the line that passes through each pair of points. The equation y = − ½x is in y = kx form. The constant variation is -1/2 The slope is,
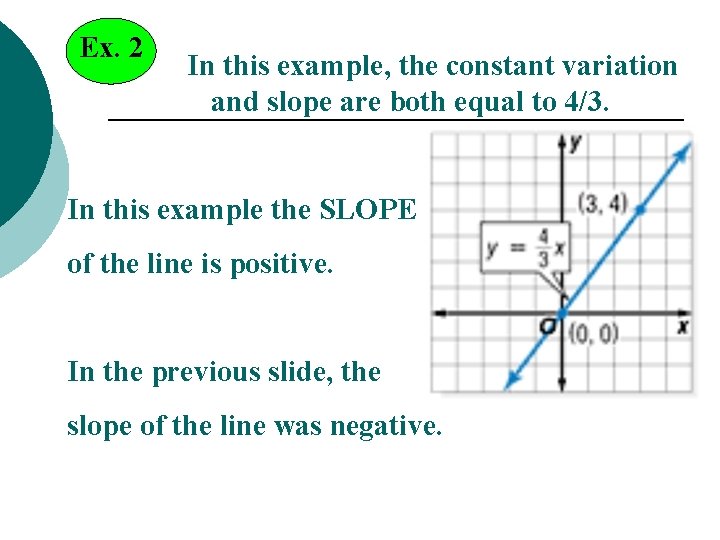
Ex. 2 In this example, the constant variation and slope are both equal to 4/3. In this example the SLOPE of the line is positive. In the previous slide, the slope of the line was negative.
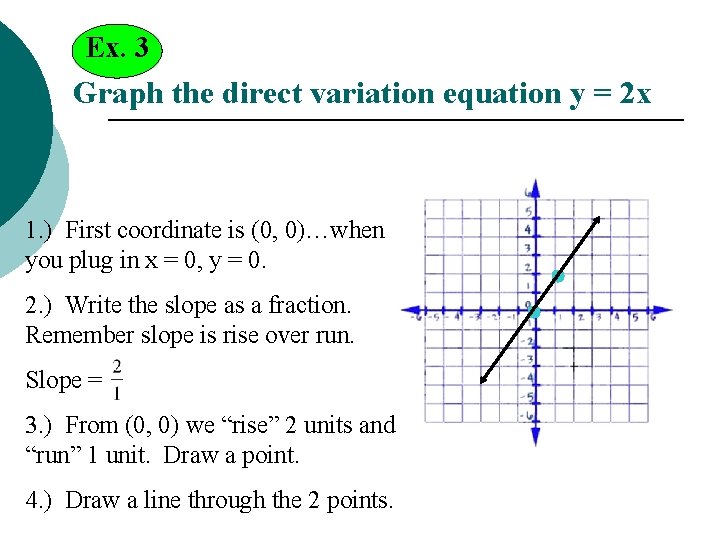
Ex. 3 Graph the direct variation equation y = 2 x 1. ) First coordinate is (0, 0)…when you plug in x = 0, y = 0. 2. ) Write the slope as a fraction. Remember slope is rise over run. Slope = 3. ) From (0, 0) we “rise” 2 units and “run” 1 unit. Draw a point. 4. ) Draw a line through the 2 points.
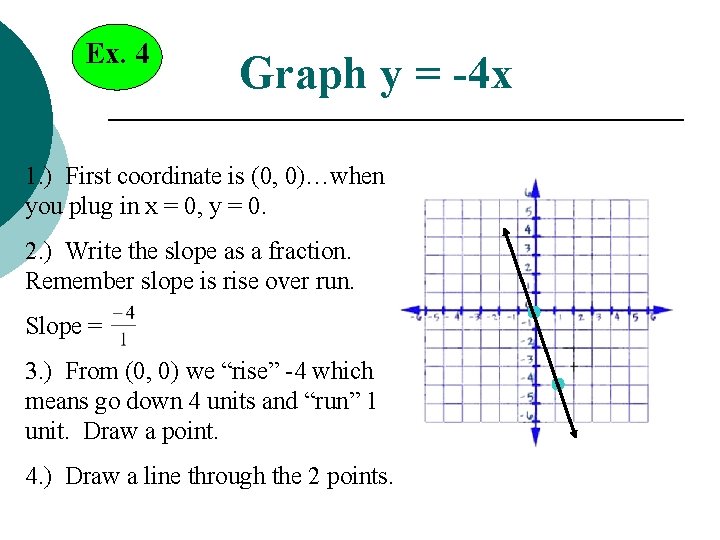
Ex. 4 Graph y = -4 x 1. ) First coordinate is (0, 0)…when you plug in x = 0, y = 0. 2. ) Write the slope as a fraction. Remember slope is rise over run. Slope = 3. ) From (0, 0) we “rise” -4 which means go down 4 units and “run” 1 unit. Draw a point. 4. ) Draw a line through the 2 points.

Ex. 5 and Solve a Direct Variation Write Equation Suppose y varies directly as x, and y = 28 and x = 7. Write a direct variation equation (y = kx) that relates x to y. We have to find the value of k first using the equation y = kx We know y = 28 and x = 7. Plug in and solve!! 28 = k ∙ 7 k=4 So the direct variation equation is y = 4 x.

Example 5 continued… Use the direct variation equation to find x when y = 52. Remember the equation we found was y = 4 x If y = 52, plug in and solve!! 52 = 4 ∙ x So x = 13, when y = 52
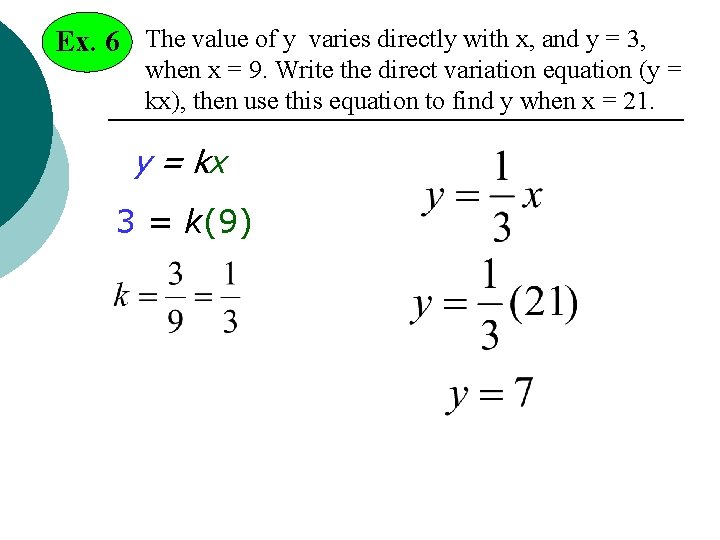
Ex. 6 The value of y varies directly with x, and y = 3, when x = 9. Write the direct variation equation (y = kx), then use this equation to find y when x = 21. y = kx 3 = k(9)

Direct Variation Equation Ex. 7 A local fast food restaurant takes in $9000 in 4 hours. a. ) Write a direct variation equation for the amount of money taken in any time. Total Income = Income per hour • $9000 = 4 k k = 2250 k • Number of hours 4 Direct variation equation: y = 2250 x, where y is total income and x is number of hours

b. ) How many hours would it take for the restaurant to earn $20, 250? y = 2250 x 20, 250 = 2250 x x = 9 hours Remember, the direct variation equation is y = 2250 x, where y is total income and x is number of hours

Assignment Study Guide 5 -2 (In-Class) ¡ Skills Practice Worksheet 5 -2 (Homework) ¡ ¡
- Slides: 14