PROBLEMAS ARITMTICOS Tema 4 4 ESO Op A

PROBLEMAS ARITMÉTICOS Tema 4 4º ESO Op A

PROBLEMAS ARITMÉTICOS 1. Proporcionalidad 1. 1. Simple 1. 2. Compuesta 2. Repartos 3. Porcentajes 4. Depósitos y préstamos bancarios 5. Mezclas 6. Móviles 7. Llenado / vaciado de depósitos

PROBLEMAS ARITMÉTICOS 1. Proporcionalidad 1. 1. Simple 1. 2. Compuesta Dos variables Directa o Inversa Tres variables Directa o Inversa Directa: Si una magnitud aumenta, la otra aumenta Si una magnitud disminuye, la otra disminuye Inversa: Si una magnitud aumenta, la otra disminuye Si una magnitud disminuye, la otra aumenta

PROBLEMAS ARITMÉTICOS 1. Proporcionalidad Simple y Compuesta Pasos resolución de problemas 1. Identificar las magnitudes del problema y explicar brevemente su relación, diciendo si es directa o inversa 2. Planteamiento del problema por regla de tres (se puede hacer en el primer lugar si así se desea) 3. Resolución del problema 4. Establecer la solución al problema

PROPORCIONALIDAD SIMPLE Directa / Inversa Ejemplo 1. Se sabe que la altura y la sombra de un edificio son proporcionales. Si la sombra de un edificio de 30 metros mide 8 metros, ¿qué altura tendrá otro edificio cuya sombra en el mismo momento mide 12 metros? 1. Identificar las magnitudes del problema y explicar brevemente su relación, diciendo si es directa o inversa A más altura del edificio, más sombra proyecta => P. Directa 2. Planteamiento del problema por regla de tres Altura (m) x 30 Sombra (m) 12 8 3. Resolución del problema Otra forma: 30 * 12 = 8 * x 4. Establecer la solución al problema Solución: La altura será de 45 metros

PROPORCIONALIDAD SIMPLE Directa Ejemplo 1. Se sabe que la altura y la sombra de un edificio son proporcionales. Si la sombra de un edificio de 30 metros mide 8 metros, ¿qué altura tendrá otro edificio cuya sombra en el mismo momento mide 12 metros? A más altura del edificio, más sombra proyecta Directa Altura (m) Sombra (m) x 12 30 8 Solución: La altura será de 45 metros => P.
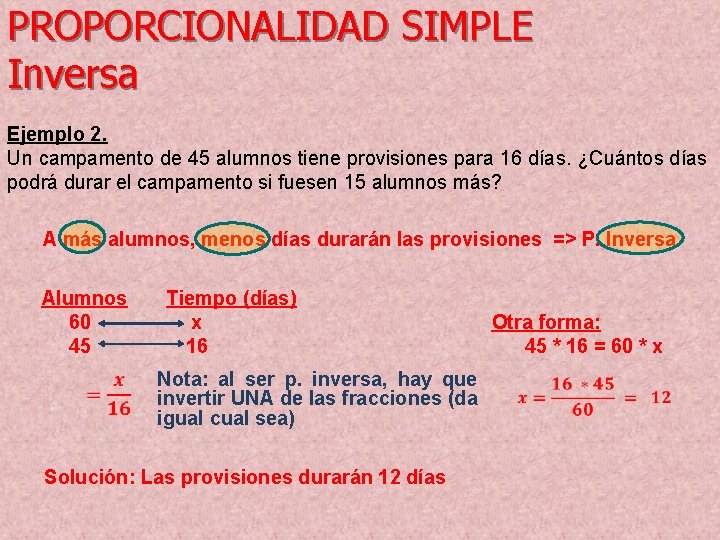
PROPORCIONALIDAD SIMPLE Inversa Ejemplo 2. Un campamento de 45 alumnos tiene provisiones para 16 días. ¿Cuántos días podrá durar el campamento si fuesen 15 alumnos más? A más alumnos, menos días durarán las provisiones => P. Inversa Alumnos 60 45 Tiempo (días) x 16 Nota: al ser p. inversa, hay que invertir UNA de las fracciones (da igual cual sea) Solución: Las provisiones durarán 12 días Otra forma: 45 * 16 = 60 * x

PROPORCIONALIDAD COMPUESTA Directa Ejemplo 3. Cuatro chicos durante 10 días de campamento han gastado en comer 60€. En las mismas condiciones, ¿cuánto gastarán en comer 6 chicos durante 15 días de campamento? . A más chicos (mismo tiempo), más dinero gastarán A más días (mismos niños), más dinero gastarán Dinero (€) x 60 Chicos 6 4 Solución: Gastarán 135 € Tiempo (días) 15 10 P. Directa

PROPORCIONALIDAD COMPUESTA Inversa Ejemplo 4 16 obreros trabajando 6 horas diarias, tardan 30 días en realizar un trabajo. ¿Cuántos días tardarán en hacer el mismo trabajo 10 obreros, empleando 8 horas diarias? A más trabajadores (mismas horas), menos días tardarán => A más horas (mismos trabajadores), menos días tardarán => Tiempo (días) x 30 Trabajadores 10 16 Solución: emplearán 36 días Tiempo (horas) 8 6 P. Inversa

PROPORCIONALIDAD COMPUESTA Directa / Inversa Ejemplo 5. En una cadena de montaje, 9 obreros trabajando 7 horas diarias han fabricado 2800 piezas. ¿Cuántos obreros son necesarios para fabricar 4000 piezas trabajando 9 horas diarias? A más trabajadores (mismas horas), más piezas harán => P. Directa A más trabajadores (mismas piezas), menos tiempo tardarán => P. Inversa Trabajadores x 9 Tiempo (horas) 9 7 Solución: serán 10 trabajadores Piezas 4000 2800

PROPORCIONALIDAD COMPUESTA Directa / Inversa Ejemplo 6 Un pintor pinta una pared de 450 m 2 en 6 días trabajando 9 horas al día. Le sale una propuesta de trabajo en la que tiene que pintar 660 m 2 en 9 días. ¿Cuántas horas diarias tiene que trabajar para poder realizar el trabajo? . A más superficie (mismos días), más horas necesita => P. Directa A más días (misma superficie), menos horas necesita => P. Inversa Tiempo (horas) x 9 Tiempo (días) 9 6 Solución: serán 8 horas diarias Superficie (m 2) 600 450

PROBLEMAS ARITMÉTICOS 1. Proporcionalidad 1. 1. Simple 1. 2. Compuesta 2. Repartos: Directo e Inverso 3. Porcentajes 4. Depósitos y préstamos bancarios 5. Mezclas 6. Móviles 7. Llenado / vaciado de depósitos

PROBLEMAS ARITMÉTICOS 2. Reparto Pasos resolución de problemas 1. Identificar la forma en que se va a repartir lo que se cita en el problema en caso de que NO nos lo digan. 2. Suma de las cantidades sobre las que se va a repartir de manera directa o sobre los inversos de las cantidades si es inversa. 3. Calculo de lo que vale una unidad de lo que se va a repartir 4. Cálculo de lo que le corresponde a cada uno según sea directo o inverso

REPARTO DIRECTAMENTE PROPORCIONAL Ejemplo 7. Un padre quiere repartir 36 galletas entre sus dos hijos de 2 y 7 años, de manera proporcional a sus edades. ¿Cuánto le toca a cada uno? 1. Identificar la forma en que se va a repartir lo que se cita en el problema en caso de que no nos lo digan. A más edad del niño, más galletas le tocarán => R. Directa 2. Suma de las cantidades sobre las que se va a repartir de manera directa 2+7=9 (se va a repartir según los años) 3. Calculo de lo que vale una unidad de lo que se va a repartir 4. . Cálculo de lo que le corresponde a cada uno 2*4=8 7 * 4 = 28 5. Establecer la solución al problema Solución: al de 2 años le da 8 galletas y al de 7 años 28 galletas

REPARTO DIRECTAMENTE PROPORCIONAL Ejemplo 7. Un padre quiere repartir 36 galletas entre sus dos hijos de 2 y 7 años, de manera proporcional a sus edades. ¿Cuánto le toca a cada uno? A más edad del niño, más galletas le tocarán Total edades => R. Directa 2+7=9 Cálculo por niño 2*4=8 7 * 4 = 28 Solución: al de 2 años le da 8 galletas y al de 7 años 28 galletas

REPARTO DIRECTAMENTE PROPORCIONAL Ejemplo 7. – Otra forma Un padre quiere repartir 36 galletas entre sus dos hijos de 2 y 7 años, de manera proporcional a sus edades. ¿Cuánto le toca a cada uno? A más edad del niño, más galletas le tocarán Total edades => R. Directa 2+7=9 Solución: al de 2 años le da 8 galletas y al de 7 años 28 galletas

REPARTO INVERSAMENTE PROPORCIONAL Ejemplo 8. Un padre quiere repartir 36 galletas entre sus dos hijos de 2 y 7 años, de manera inversamente proporcional a sus edades. ¿Cuánto le toca a cada uno? (Reparto inverso: lo dice el enunciado) Se reparte según los años pero INVERSAMENTE a ellos Solución: al de 2 años le da 28 galletas y al de 7 años 8 galletas

REPARTO INVERSAMENTE PROPORCIONAL Ejemplo 8. – Otra forma Un padre quiere repartir 36 galletas entre sus dos hijos de 2 y 7 años, de manera inversamente proporcional a sus edades. ¿Cuánto le toca a cada uno? (Reparto inverso: lo dice el enunciado) Solución: al de 2 años le da 28 galletas y al de 7 años 8 galletas

REPARTO PROPORCIONAL Ejemplo 9 La inversión de 5 socios en un negocio ha sido de 80, 60, 45, 40 y 25 miles de euros respectivamente. Deciden repartir una ganancia de 42. 000 € de manera proporcional al dinero aportado. Sin embargo, Juan, que invirtió 45. 000 € piensa que le hubiera correspondido más dinero si el reparto hubiera sido de manera inversamente proporcional. Razona si Juan tiene razón o no: calcula lo que ‘gana o pierde’ según lo que piensa

REPARTO PROPORCIONAL Solución: Juan hubiera ganado más dinero con un reparto inversamente proporcional

PROBLEMAS ARITMÉTICOS 1. Proporcionalidad 1. 1. Simple 1. 2. Compuesta 2. Repartos 3. Porcentajes 4. Depósitos y préstamos bancarios 5. Mezclas 6. Móviles 7. Llenado / vaciado de depósitos

PROBLEMAS ARITMÉTICOS 3. Porcentajes

PROBLEMAS ARITMÉTICOS 3. Porcentajes • Aumento porcentual: Resultado de sumar un porcentaje al 100%, cuando éste, represente una variación al alza Por ejemplo: Una prenda aumenta un 12% El aumento será del 12% + 100% = 112% • Disminución porcentual: Resultado de restar un porcentaje al 100%, cuando éste, represente una variación a la baja Por ejemplo: Una prenda se rebaja un 12% La disminución será del 100% - 12% = 88%

PROBLEMAS ARITMÉTICOS 3. Porcentajes • Índice de variación (IV): «Cuando se producen aumentos y/o disminuciones porcentuales seguidas sobre un mismo artículo» . Se expresa como un número decimal calculado como resultado de la multiplicación de todos los aumentos y todas las disminuciones porcentuales que sufre el artículo.

PROBLEMAS ARITMÉTICOS 3. Porcentajes • Índice de variación (IV): Por ejemplo: Una prenda aumenta un 12%, luego sube otro 20% y al final es rebajada un 30% El aumento del 12% sería un 112% = 1, 12 El aumento del 20% sería un 120% = 1, 20 La disminución del 30% sería un 70% = 0, 70 El IV sería 1, 12 * 1, 20 * 0, 70 = 0, 9408 Si se multiplica por 100, el porcentaje resultante es el que representa la variación real del artículo 0, 9408 => 94, 08 %

PROBLEMAS ARITMÉTICOS 3. Porcentajes • Índice de variación (IV): Por ejemplo: Una prenda vale 120 €. Aumenta un 50% y luego es rebajada un 50% ¿Se queda al mismo precio? El aumento del 50% sería un 150% = 1, 50 La disminución del 50% sería un 50% = 0, 50 El IV sería 1, 50 * 0, 50 = 0, 75 Si se multiplica por 100, el porcentaje resultante es el que representa la variación real del artículo 0, 75 => 75 % No se queda al mismo precio. La prenda costará ahora 90€

PROBLEMAS ARITMÉTICOS Ejemplo 10. Vas a la tienda a comprar leche de la marca que quieres y te encuentras con dos ofertas. Por supuesto, quieres ahorrarte dinero comprando la más barata y la cantidad de brics que te lleves te da igual. ¿Cuál de las ofertas elegirías? . Precio unitario de la caja de leche en ambos casos: 0, 58 € Oferta A Oferta B 3 x 2 - 75% Compra 2 y te llevas 3 En la segunda unidad 1. Oferta A Solución: La mejor es la oferta B 2. Oferta B

PROBLEMAS ARITMÉTICOS 1. Proporcionalidad 1. 1. Simple 1. 2. Compuesta 2. Repartos 3. Porcentajes 4. Depósitos y préstamos bancarios 5. Mezclas 6. Móviles 7. Llenado / vaciado de depósitos

PROBLEMAS ARITMÉTICOS 4. Depósitos y préstamos bancarios Conceptos - Co: Capital inicial del que se parte - C: Capital final obtenido tras el préstamo / depósito - r: Es el interés que se aplica sobre el depósito / préstamo en % - t: es el tiempo sobre el que se calcula el depósito / préstamo

PROBLEMAS ARITMÉTICOS 4. Depósitos y préstamos bancarios Dos tipos: a) INTERÉS SIMPLE Se retira el capital al final del periodo considerado b) INTERÉS COMPUESTO NO se retira el capital al final del periodo considerado El capital final, pasa a ser el capital inicial para el nuevo periodo, y así sucesivamente hasta que se decide retirarlo o se acaba el contrato.

PROBLEMAS ARITMÉTICOS 4. Depósitos y préstamos bancarios Dos tipos: - Consideramos en ambos caso el periodo anual a) INTERÉS SIMPLE b) INTERÉS COMPUESTO

PROBLEMAS ARITMÉTICOS 4. Depósitos y Préstamos bancarios Pasos resolución de problemas 1. Identificar los datos del enunciado 2. Identificar la fórmula a usar según sea interés simple o compuesto 3. Cálculo de lo que nos solicitan según la fórmula a usar 4. Dar la solución al problema

DEPÓSITOS Y PRÉSTAMOS BANCARIOS Ejemplo 11. Se dejan el banco 10000€ a un interés simple anual del 2%. Calcular el capital final a los 3 años 1. Identificar los datos del enunciado - Co: Capital inicial = 10000€ - r: Interés aplicado = 2% - t: Tiempo = 3 años Interés Simple 2. Cálculo de lo solicitado 3. Dar la solución al problema Solución: Capital final es de 10600 €

DEPÓSITOS Y PRÉSTAMOS BANCARIOS Ejemplo 12. Se dejan el banco 10000€ a un interés compuesto anual del 2%. Calcular el capital final a los 3 años 1. Identificar los datos del enunciado - Co: Capital inicial = 10000€ - r: Interés aplicado = 2% - t: Tiempo = 3 años Interés Compuesto 2. Cálculo de lo solicitado 3. Dar la solución al problema Solución: Capital final es de 10612, 08 €

DEPÓSITOS Y PRÉSTAMOS BANCARIOS Ejemplo 13. Un capital de 120000 €, colocado en una cuenta a un tres años, se convierte en 126750 €. ¿Qué tanto por ciento anual abona la cuenta? 1. Identificar los datos del enunciado - Co: Capital inicial = 120000€ - C: Capital final = 126750 € - t: Tiempo = 3 años Interés Compuesto 2. Cálculo de lo solicitado 3. Dar la solución al problema Solución: el interés es del 1, 84%

PROBLEMAS ARITMÉTICOS 1. Proporcionalidad 1. 1. Simple 1. 2. Compuesta 2. Repartos 3. Porcentajes 4. Depósitos y préstamos bancarios 5. Mezclas 6. Móviles 7. Llenado / vaciado de depósitos

PROBLEMAS ARITMÉTICOS 5. Mezclas - Intervienen dos o más elementos que deben ser mezclados - Se obtiene un ‘’nuevo elemento’’ que es la mezcla de todos los iniciales - La cantidad total de la mezcla será la suma de las cantidades mezcladas - El precio total, estará entre los valores de los elementos mezclados - Se organizan los datos en una tabla para una visión global del problema

MEZCLAS Ejemplo 14. Se mezclan 20 litros de aceite de 3, 9 €/litro y 50 litros de otro aceite de inferior calidad, de 2, 40 €/litro. ¿A cómo resulta el litro de la mezcla obtenida? . 1. Poner los datos en forma de tabla Cantidad (l) Precio (€/l) Coste (€) Aceite 1 20 3, 9 20*3, 9 = 78 Aceite 2 50 2, 4 50*2, 4 = 120 Mezcla 70 x 2. Cálculo de lo solicitado 70 * x = 198 x = 2, 8285 3. Dar la solución al problema 198 => x = 2, 83 €/litro Solución: el litro resulta a 2, 83 €/litro

PROBLEMAS ARITMÉTICOS 1. Proporcionalidad 1. 1. Simple 1. 2. Compuesta 2. Repartos 3. Porcentajes 4. Depósitos y préstamos bancarios 5. Mezclas 6. Móviles 7. Llenado / vaciado de depósitos

PROBLEMAS ARITMÉTICOS 6. Móviles

PROBLEMAS ARITMÉTICOS 6. Móviles – Dos tipos de problemas

PROBLEMAS ARITMÉTICOS 6. Móviles – Dos tipos de problemas a) Por ALCANCE: «Un móvil va detrás de otro (en el mismo sentido), y al final, le alcanza» . La velocidad total será la RESTA de las velocidades de ambos móviles Velocidad total será: Velocidad: t = tiempo en recorrer ‘e’ a una velocidad ‘v 3’ v 3 = v 2 –v 1 v 2 Nota: v 2 > v 1 = velocidad del móvil 1 (el que va primero) v 2 = velocidad del móvil 2 (el que persigue - va más rápido y le alcanza) e A v 3 = v 2 – v 1 B v 1

PROBLEMAS ARITMÉTICOS 6. Móviles – Dos tipos de problemas b) Por ENCUENTRO: «Un móvil va en un sentido, y el otro móvil, va en el contrario. Llega un momento que se cruzan» . La velocidad total será la SUMA de las velocidades de ambos móviles Velocidad total será: Velocidad: v 1 = velocidad del móvil 1 v 2 = velocidad del móvil 2 e t = tiempo en recorrer ‘e’ a una velocidad ‘v 3’ v 3 = v 2 + v 1 A v 2 v 3 = v 2 + v 1 B v 1

PROBLEMAS ARITMÉTICOS 6. Móviles Pasos resolución de problemas 1. Identificar si el problema es de alcance o de persecución 2. IMPORTANTE: Usar las unidades de medida de manera homogénea (todo en metros / todo en kilómetros / todo en …) 3. Cálculo de la nueva velocidad (v 3), en caso de requerirse 4. Aplicar las fórmulas dadas 5. Dar la solución al problema

MÓVILES Ejemplo 15. Un coche circula a 100 km/h y se mueve en la misma dirección que otro que circula a 25 m/s. Si la distancia que les separa son 90 km, calcular cuánto tardará en adelantarle. 1. Identificar el problema: es de alcance 2. Usar las mismas unidades de velocidad, de espacio y de tiempo v 1 = 25 m/s = 25 * 3, 6 km/h = 90 km/h v 2 = 100 km/h 3. Calculamos la velocidad v 3 = v 2 – v 1 = 100 – 90 = 10 km/h 4. Cálculo del tiempo e=v*t 90 = 10 * t 5. Dar la solución al problema t = 9 horas Solución: 9 horas e = 90 km

MÓVILES Ejemplo 16. Un coche sale de la ciudad A hacia la ciudad B a las 15 h, a una velocidad de 100 km/h. En ese instante, otro vehículo, sale de B a A, a 30 m/s. Si la distancia entre ambas ciudades es de 676 km, calcular cuándo se cruzarán. 1. Identificar el problema: es de encuentro 2. Usar las mismas unidades de velocidad, de espacio y de tiempo v 1 = 30 m/s = 30 * 3, 6 km/h = 108 km/h v 2 = 100 km/h e = 676 km 3. Calculamos la velocidad v 3 = v 2 + v 1 = 108 + 100 = 208 km/h 4. . Cálculo del tiempo e=v*t 676 = 208 * t La parte decimal son 5. Dar la solución al problema t = 3, 25 horas t = 0, 25 horas = 0, 25*60 = 15 minutos Solución: se cruzan a las 18 h y 15 minutos

PROBLEMAS ARITMÉTICOS 1. Proporcionalidad 1. 1. Simple 1. 2. Compuesta 2. Repartos 3. Porcentajes 4. Depósitos y préstamos bancarios 5. Mezclas 6. Móviles 7. Llenado / vaciado de depósitos

PROBLEMAS ARITMÉTICOS 7. Llenado y vaciado de depósitos

PROBLEMAS ARITMÉTICOS 7. Llenado y vaciado de depósitos - Escala de volumen: km 3 hm 3 dam 3 dm 3 cm 3 mm 3 litro ml Cada ‘salto’ vale 1000 unidades - Nota: 1 litro (l) = 1 dm 3 1 mililitro (ml) = 1 cm 3 - Escala de tiempo: 1 h = 60’ = 3600’’ - El llenado de un depósito implica la suma de los caudales de todos los elementos que llenan el depósito - El vaciado implica restar el caudal que ‘sale’ del depósito

PROBLEMAS ARITMÉTICOS 7. Llenado y vaciado de depósitos Pasos resolución de problemas 1. Identificar los datos que implican llenado y que implican el vaciado 2. Llenado: suma cantidades Vaciado: resta cantidades 3. Resolución del problema 4. Dar la solución al problema

LLENADO Y VACIADO DE DEPÓSITOS Ejemplo 17. Una piscina se abastece mediante dos bombas, A y B. La primera bomba, trabajando sola, llena la piscina en cinco horas, y la segunda, también en solitario, tarda tres horas. ¿Cuánto tardará en llenarse la piscina si ambas se conectan simultáneamente? . 1. Identificar los datos que implican llenado y que implican el vaciado 2. Calculamos A + B (ambas son llenado) 3. Cálculo del tiempo total 5. Dar la solución al problema Solución: llenan la piscina en 1 h 52, 5 minutos

LLENADO Y VACIADO DE DEPÓSITOS Ejemplo 18. Una bañera dispone de un grifo de agua fría y otro de agua caliente. Abriendo solo el agua fría, se llena en 8 minutos, y abriendo la caliente, en 12 minutos. Dispone también de un desagüe que, cuando está llena, la vacía en 4 minutos. a) ¿Cuánto tiempo tarda en llenarse si se abren los dos grifos a la vez para obtener agua templada? b) ¿Qué ocurrirá si, estando vacía, se abren los dos grifos y se olvida colocar el tapón del desagüe?

LLENADO Y VACIADO DE DEPÓSITOS Ejemplo 19. Una bañera dispone de un grifo de agua fría y otro de agua caliente. Abriendo solo el agua fría, se llena en 8 minutos, y abriendo la caliente, en 12 minutos. Dispone también de un desagüe que, cuando está llena, la vacía en 4 minutos. a) ¿Cuánto tiempo tarda en llenarse si se abren los dos grifos a la vez para obtener agua templada? b) ¿Qué ocurrirá si, estando vacía, se abren los dos grifos y se olvida colocar el tapón del desagüe?

PROBLEMAS ARITMÉTICOS Tema 4 4º ESO Op A
- Slides: 54