Problem Solving thru Programming HCJC Creative Problem Solving

Problem Solving thru Programming @ HCJC Creative Problem Solving in Computing Leong Hon Wai Department of Computer Science School of Computing National University of Singapore 8 March 2003 http: //www. comp. nus. edu. sg/~leonghw/ leonghw@comp. nus. edu. sg (Problem Solving) Page 1 © Leong Hon Wai, 2003 -2005

Outline v Polya’s Problem Solving Framework q Four Stages in Problem Solving q Solving Problems by Asking More Questions! q Examples v Is Problem Solving still important q Now we have very fast computers, grids v Any real differences between O(n 2) and O(n lg n) q Some examples: Google and the Human Genome Project (Problem Solving) Page 2 © Leong Hon Wai, 2003 -2005

Quote A great discovery solves a great problem, but there is a grain of discovery in the solution of any problem. Your problem may be modest; but if it challenges your curiosity and bring into play your inventive faculties, and if you solve it by your own means, you may experience the tension and enjoy the triumph of discovery. G. Polya, 1945 (Problem Solving) Page 3 © Leong Hon Wai, 2003 -2005
Four Stages of Problem Solving (G. Polya) G. Polya, “How to Solve It”, Princeton Univ Press, 1945 v Stage 1: Understanding the Problem v Stage 2: Devising a Plan v Stage 3: Carrying out the Plan v Stage 4: Looking Back The most widely cited reference for problem solving in all disciplines (Problem Solving) Page 4 © Leong Hon Wai, 2003 -2005

More on “Four Stages” (Problem Solving) Page 5 © Leong Hon Wai, 2003 -2005

Problem 1: An “Impossible Problem” What is (11… 1) (100… 05) + 1 100 1’s 99 0’s v Quick: Get the calculator… q Not so useful… v Polya Question: Look at the data? (stare at it !!) q (111… 1)(100… 05) + 1 ? ? q Let’s call it “something-big” v PQ: What is the unknown? q Is it an integer? …a real number? (Problem Solving) Page 6 © Leong Hon Wai, 2003 -2005

An “Impossible Problem” (2) What is (11… 1) (100… 05) + 1 100 1’s 99 0’s v PQ: Can you re-state the problem? or unknown? q To find the square-root of “something-big plus 1” v PQ: What is that “something-big”? q Don’t know, but it is q “(square of ‘some-other-thing’) minus 1” v PQ: Shall we introduce notations: q “ y 2 – 1 ” = (y + 1)(y – 1) q It is also (11… 1)*(100… 05) (Problem Solving) Page 7 © Leong Hon Wai, 2003 -2005

Something-big plus 1 v PQ: Can we try some special cases? (1)(15)+1 (11)*(105)+1 = 1 (3 * 5)+1 = (4 -1)(4+1)+1 = 4**2 -1+1 = 11*(99+6)+1 = 11*3*(33+2)+1 = 33*(33+2)+1 = (34 -1)(34+1)+1 = 34**2 -1+1 (111)*(1005)+1 = 111*(999+6)+1 = 333*(333+2)+1 = (334 -1)(334+1)+1 = 334**2 (1111)*(10005)+1 = 1111*(9999+6)+1 = 3333*(3333+2)+1 = (3334 -1)(3334+1)+1 = 3334**2 Get the pattern? … can u prove it? (Problem Solving) Page 8 © Leong Hon Wai, 2003 -2005

Looking Back v Looking Back: Where is the Key Idea? q (y 2 - 1) = (y-1)(y+1) !!! v Can I do it differently? q Define something -- maybe 111… 1 q (111…. 1) (1000… 05) + 1 So, let X = 111… 1 q Something-big + 1 = X (999… 9 + 6) + 1 = X (9 X + 6) + 1 = 9 X 2 + 6 X + 1 = (3 X+1)^2 q So, y = 3 X+1. Viola!!! (Problem Solving) Page 9 © Leong Hon Wai, 2003 -2005
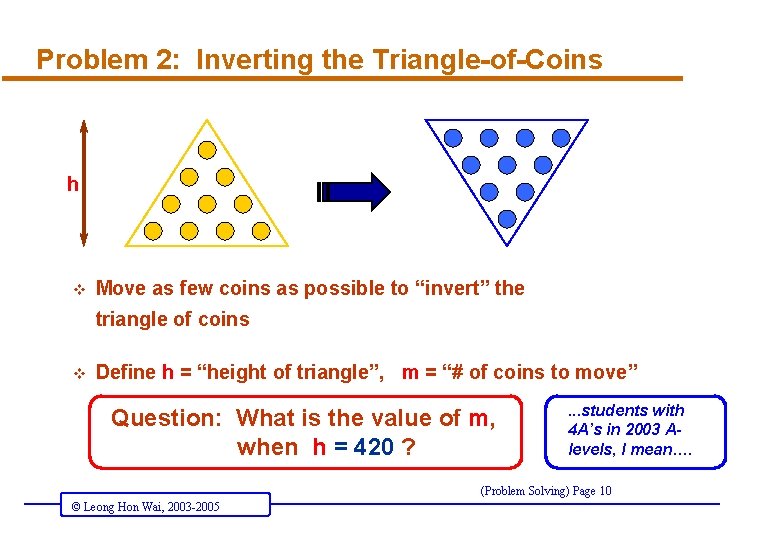
Problem 2: Inverting the Triangle-of-Coins h v Move as few coins as possible to “invert” the triangle of coins v Define h = “height of triangle”, m = “# of coins to move” Question: What is the value of m, when h = 420 ? . . . students with 4 A’s in 2003 Alevels, I mean…. (Problem Solving) Page 10 © Leong Hon Wai, 2003 -2005
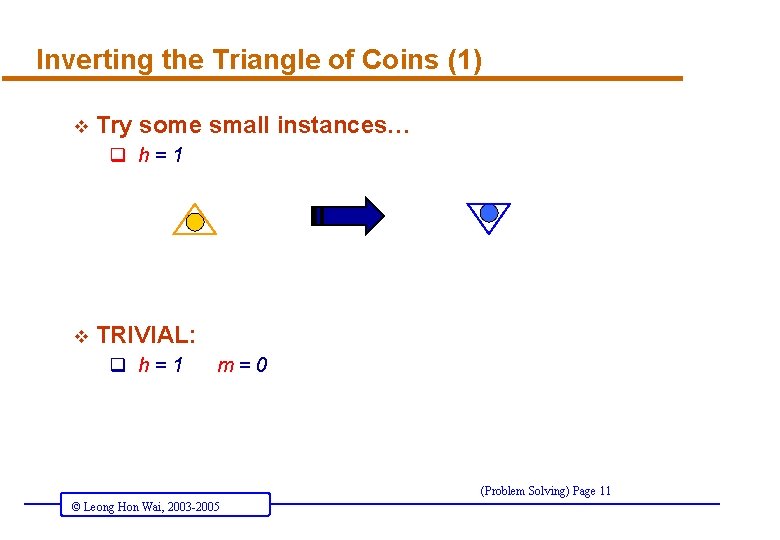
Inverting the Triangle of Coins (1) v Try some small instances… q h=1 v TRIVIAL: q h=1 m=0 (Problem Solving) Page 11 © Leong Hon Wai, 2003 -2005
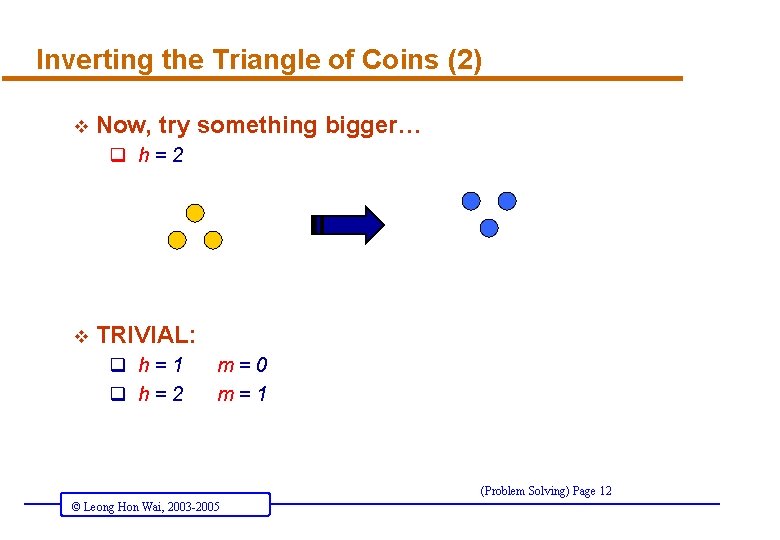
Inverting the Triangle of Coins (2) v Now, try something bigger… q h=2 v TRIVIAL: q h=1 q h=2 m=0 m=1 (Problem Solving) Page 12 © Leong Hon Wai, 2003 -2005
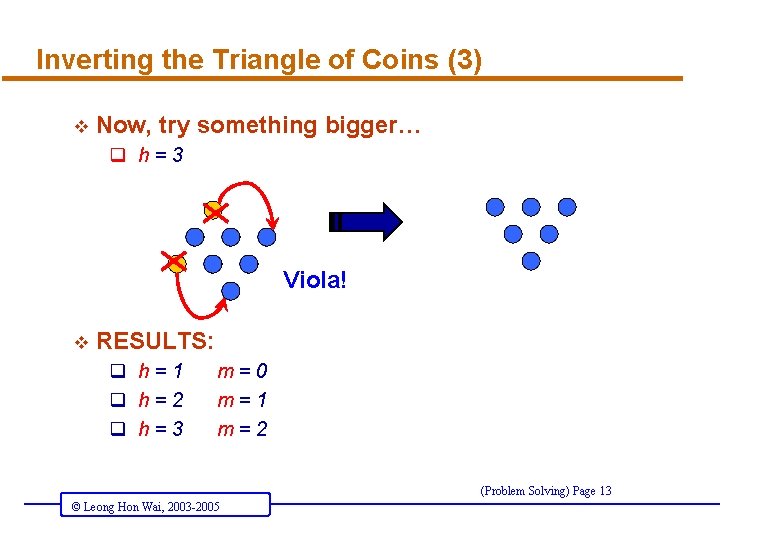
Inverting the Triangle of Coins (3) v Now, try something bigger… q h=3 Viola! v RESULTS: q h=1 q h=2 q h=3 m=0 m=1 m=2 (Problem Solving) Page 13 © Leong Hon Wai, 2003 -2005
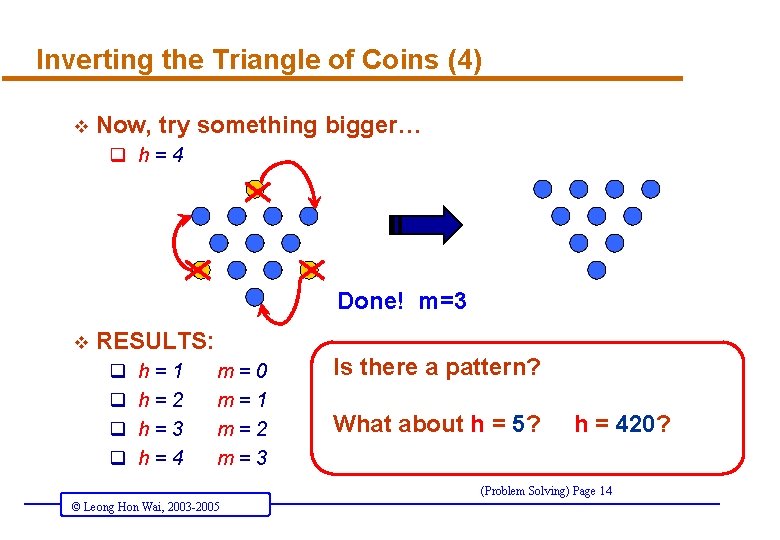
Inverting the Triangle of Coins (4) v Now, try something bigger… q h=4 Done! m=3 v RESULTS: q q h=1 h=2 h=3 h=4 m=0 m=1 m=2 m=3 Is there a pattern? What about h = 5? h = 420? (Problem Solving) Page 14 © Leong Hon Wai, 2003 -2005
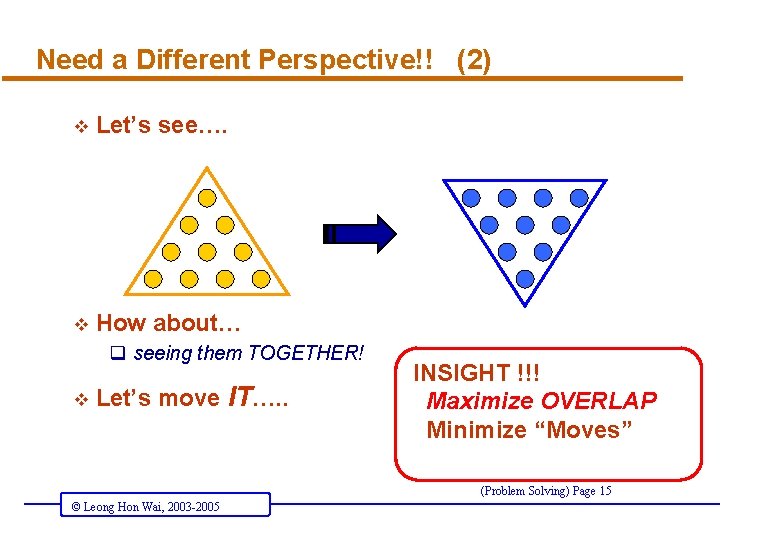
Need a Different Perspective!! (2) v Let’s see…. v How about… q seeing them TOGETHER! v Let’s move IT…. . INSIGHT !!! Maximize OVERLAP Minimize “Moves” (Problem Solving) Page 15 © Leong Hon Wai, 2003 -2005
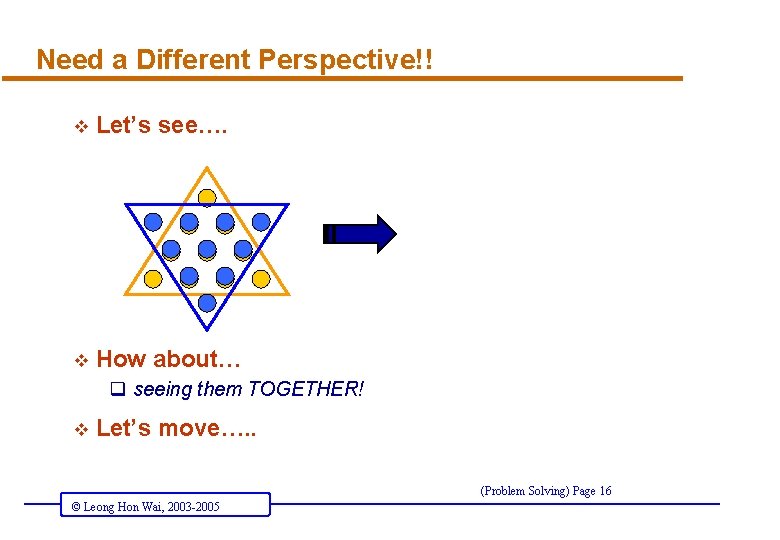
Need a Different Perspective!! v Let’s see…. v How about… q seeing them TOGETHER! v Let’s move…. . (Problem Solving) Page 16 © Leong Hon Wai, 2003 -2005
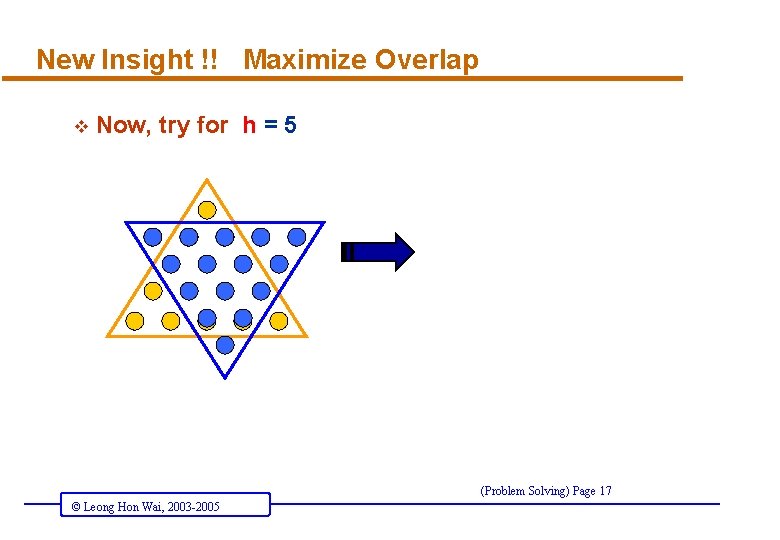
New Insight !! Maximize Overlap v Now, try for h = 5 (Problem Solving) Page 17 © Leong Hon Wai, 2003 -2005

New Insight !! Maximize Overlap v There are 3 sides in a triangle. q At each side, we have a “non-overlapping” triangle! q Denote their heights (a, b, c) (0, 1, 3) (1, 1, 2) (0, 0, 4) (Problem Solving) Page 18 © Leong Hon Wai, 2003 -2005
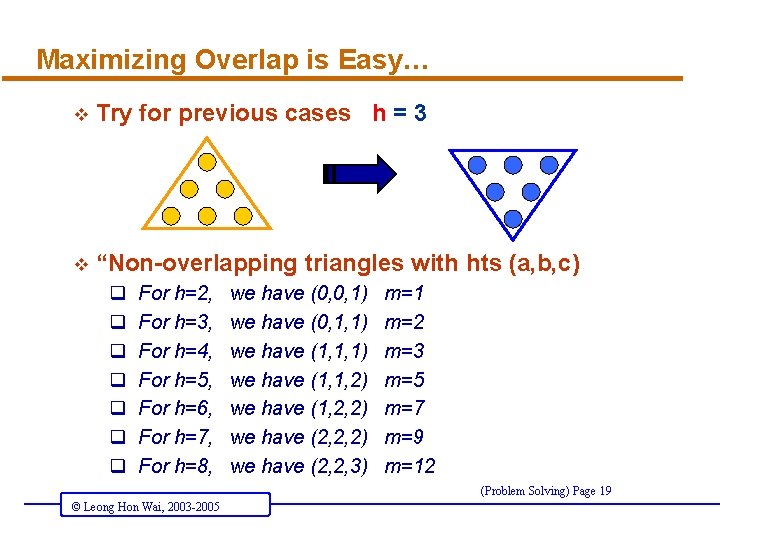
Maximizing Overlap is Easy… v Try for previous cases h = 3 v “Non-overlapping triangles with hts (a, b, c) q q q q For h=2, For h=3, For h=4, For h=5, For h=6, For h=7, For h=8, we have (0, 0, 1) we have (0, 1, 1) we have (1, 1, 2) we have (1, 2, 2) we have (2, 2, 3) m=1 m=2 m=3 m=5 m=7 m=9 m=12 (Problem Solving) Page 19 © Leong Hon Wai, 2003 -2005

Looking Back…. v Can work out for h = 9, 10, 11, 12, …, 420 v ANSWER is NOT so important, the METHOD IS v Where is the Key Step ? v Why was it not apparent to us at the beginning ? v How did we get to this step ? (Problem Solving) Page 20 © Leong Hon Wai, 2003 -2005

References…. for More readings. . . v G. Polya, “How to Solve It”, q Princeton Univ Press (1945), q re-published by Penguin Books (1990) v W. A. Wickelgren, “How to Solve Problems”, q W. H. Freeman, 1974. v R. R. Kadesch, “Problem Solving Across the Disciplines”, q Prentice Hall, 1997. v Edward De Bono, q Various Different Titles (from Lateral Thinking, to Teaching Thinking, to Hats, to Simplicity). v [Ev. An] Everywhere and Anywhere -- Use your imagination!. (Problem Solving) Page 21 © Leong Hon Wai, 2003 -2005

Problem Solving in Computing – Do we need it? v Is there a need for Problem Solving? q We have invented many algorithms over the past 50 yrs q There are many textbooks on algorithms already q Don’t we already have all the algorithms we need? v Why not let faster computer do the job? q Computer are getting faster all the time (Moore’s Law) q Current Speed: 2 Giga. FLOP (2 billion operations / sec) Ø 3 Giga. FLOP? 10 Giga. FLOP? v What about parallel processing? GRID Computing? q What is the largest GRID we have? Ø 11 Teraflop (NSF funded @ 4 centers) ? (Problem Solving) Page 22 © Leong Hon Wai, 2003 -2005

Let’s look at a popular example: Google v Google: q One of the best (if not the best) search engines q Google searches 3 x 109 pages (3, 083, 324, 652) v How big is 3 x 109 anyway? q. The size of the human genome (in terms of base-pairs) q If we print out 3 x 109 characters on A 4 paper, it will be Ø (3 x 109 / (66 x 80)) * 5 / (500 x 100) metres = 56. 8 metres Øabout a 20 -storey HDB block high! Ø Assumptions: • • 1 A 4 page = 66 rows x 80 columns 500 A 4 page = 5 cm (in height) 210 = 1000 1 yr = 3 x 106 sec (Problem Solving) Page 23 © Leong Hon Wai, 2003 -2005

O(n 2) vs O(n lg n) algorithm v If Google wants to sort the pages (say by Title) q Here n = 3 x 109 (webpages) v If we use an O(n 2) algorithm q On a very fast computer (say, 3 Giga. FLOP) Ø (3 x 109 ) / (3 x 109) (3 x 107) = 100 years Ø 30 years if it is 10 Giga. FLOP q On world’s largest GRID Cluster: 11 x 1012 (tera. FLOP) Ø 3 months (assuming no time lost among cluster) v If we use an O(n lg n) algorithm q (3 x 109) x 30 / (3 x 109) = 30 seconds q Don’t need GRID (Problem Solving) Page 24 © Leong Hon Wai, 2003 -2005

Other examples of O(n 2) and O(n lg n) v FM (higher quality sound) q Uses a technique called Fast Fourier Transform (FFT) q Old method of doing transform – O(n 2) q with FFT – O(n lg n) (Problem Solving) Page 25 © Leong Hon Wai, 2003 -2005
Human Genome Project (Problem Solving) Page 26 © Leong Hon Wai, 2003 -2005

Human Genome Project v Human Genome Project (1986 -2003) q 3 x 109 base-pairs q 24 chromosomes q 30 K – 40 K genes (ave 3000 bp each) v Goals: q Identify the genes, DNA sequence q Develop tools to help data analysis q Interpret results in biologically meaningful manner (Problem Solving) Page 27 © Leong Hon Wai, 2003 -2005

HGP – A Reverse Engg. Problem v Given q 3 GB of mass storage (24 partitions) q Unknown OS, file format q Known encoding scheme q Files are fragmented q Disk has active and deleted blocks q Hardware design & system BIOS also on disk v Task: q Recover and document about 35, 000 programs that represent the OS, q Figure out the low level control code & q schematic description of how computer is put together; (Problem Solving) Page 28 © Leong Hon Wai, 2003 -2005

Computer Scientists contributes… v Human Genome Project q Original Target: end in 2005 or beyond v Enter many prominent computer scientists q Powerful algorithmic techniques, q Divide and conquer paradigms q Scalable methods for speed-ups (eg: DNA Arrays) v Outcome q June 2000 – Working Draft Sequences q Feb 2001 – published q 2003 – expect high quality version completed !! (Problem Solving) Page 29 © Leong Hon Wai, 2003 -2005

Efficient Algorithms with Arrays… v Problem: q. You have planned out a very long route that passed through a number of intermediate cities labelled 1, 2, …, n. You are given the distances d(j) where d(j) is the distance between city j and j+1. q. You receive a lot of queries of the form What is the distance between city a and city b? q Device a scheme so that you can answer all of these queries in O(1) time. (constant time). (Problem Solving) Page 30 © Leong Hon Wai, 2003 -2005

The Most Important Message of the Day… ASK QUESTIONS v Do I understand the problem ? v Do I understand their solution ? v Why does the solution work ? v justto understand Why did. Don’t he choose do this or that ? the solution, v also understand the motives How but can I try invent suchtoa solution ? v Can I do it differently ? v Can I do it more elegantly ? and procedures of arriving at the solution. (Problem Solving) Page 31 © Leong Hon Wai, 2003 -2005

Message for the Day (2) v Running time MATTERS v There are still lots of computational problems q left to be solve, and q waiting to be solved well. (Problem Solving) Page 32 © Leong Hon Wai, 2003 -2005

THANK YOU VERY MUCH And I hope to work with some of you in the future (Problem Solving) Page 33 © Leong Hon Wai, 2003 -2005
- Slides: 33

























































