Problem Solving Problem Solving definition you have a

Problem Solving

Problem Solving definition: you have a goal, and you are currently not at the goal. Want to own a dog—don’t have a dog. Need 3 -letter word for European blackbird—don’t know it Want to attend graduate school—not currently in graduate school Want to be outside—currently are inside

Problem types Well defined problem: initial state, goal state, and methods available to you are understood. Example: solving an anagram. Vince Goti Initial state: vince goti Goal state: any word Methods: rearranging

Problem types Ill defined problem: initial state, goal state, and/or methods are poorly understood. Example: writing a term paper Initial state: no paper Goal state: a paper that looks like ? Methods: ? ? ?

Approaches to problem solving • Behaviorist • Gestalt • Information processing

Behaviorist

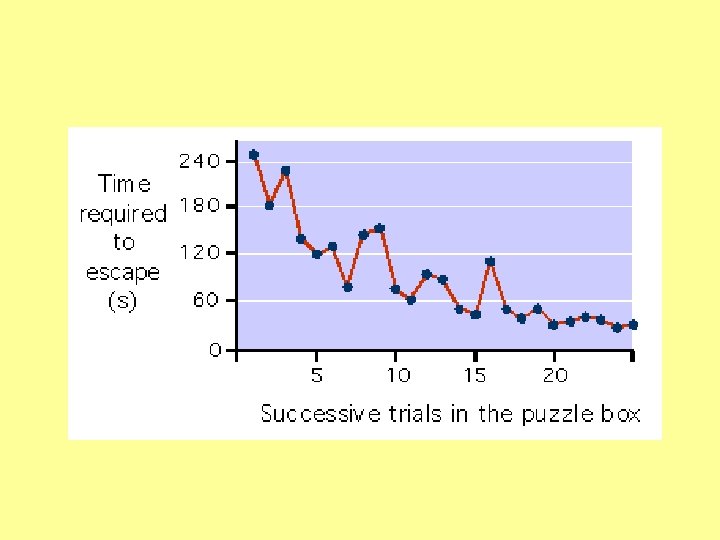
Behaviorist view Problem solving seen almost as a matter of chance early in training. Due to random variation, you produce slightly better versions; these are reinforced, so you’re more likely to do them again.

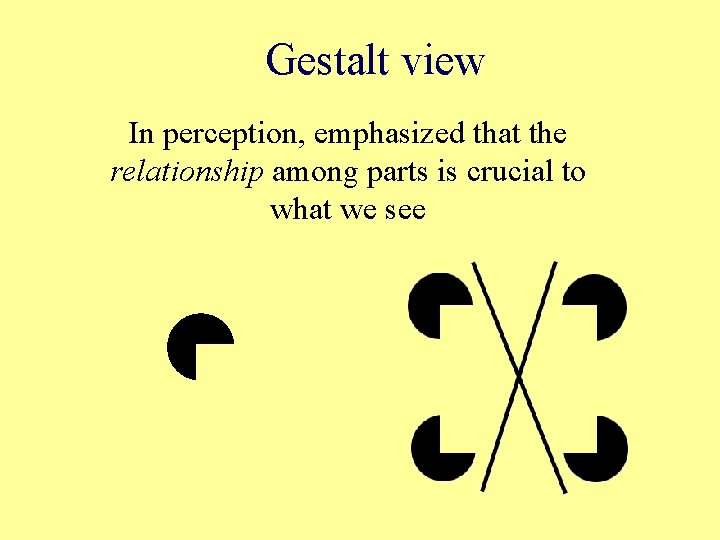
Gestalt view In perception, emphasized that the relationship among parts is crucial to what we see

Sometimes more than one organization of parts is possible; the perception can reverse. http: //dogfeathers. com/java/necker. html

Gestalt view Same emphasis in problem solving: Gestalt psychologists emphasized that the way you see the relationship of the parts of a problem dictates the difficulty of finding a solution: Sometimes you reorganize the parts, the whole looks different and the solution is easy.

Wolfgang Köhler

Two trains are 25 miles apart and are traveling towards one another. One is going 35 mph and the other is going 15 mph. A fly begins on the second train and starts to fly towards the first, traveling 20 mph. How far does the fly travel before the trains collide and it is smooshed?

Gestalt view Some problems that initially seem hard suddenly become trivial when the representation is changed. You have an “Aha!” experience.

Gestalt view says little about non-Aha problems, or about how you get the change in representation.

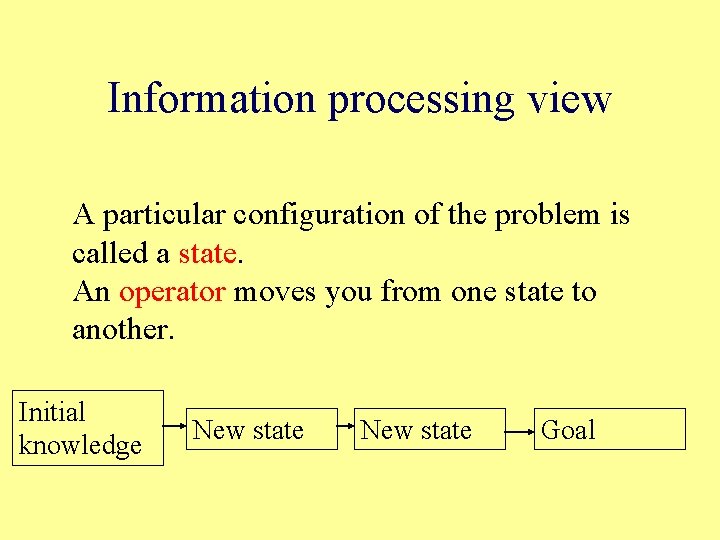
Information processing view A particular configuration of the problem is called a state. An operator moves you from one state to another. Initial knowledge New state Goal

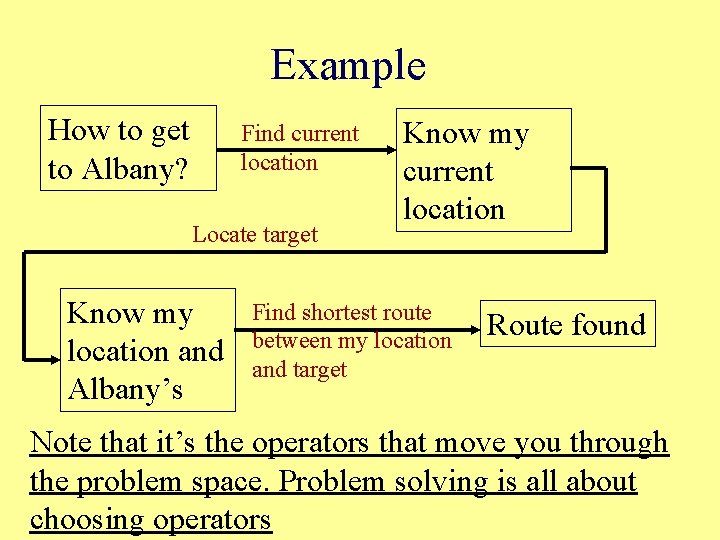
Example How to get to Albany? Find current location Locate target Know my location and Albany’s Know my current location Find shortest route between my location and target Route found Note that it’s the operators that move you through the problem space. Problem solving is all about choosing operators

This observation (that operators move you through the space) makes our job clearer: the question is how do you select operators? Three general cases we can consider: 1) Very familiar problem--algorithm 2) you have very little relevant knowledge 3) you have some relevant knowledge

Algorithm An algorithm for problem-solving is a formula —it is a fixed series of steps that you apply. If you apply them correctly, you will arrive at a solution, possibly the desired solution.

4 cups fresh or frozen tart cherries 1 to 1 1/2 cups granulated sugar 4 tablespoons cornstarch 1/8 tablespoon almond extract (optional) Your favorite pie crust or pie dough recipe for 2 crust pie 1 1/2 tablespoons butter, to dot 1 tablespoon granulated sugar, to sprinkle Place cherries in medium saucepan and place over heat. Cover. After the cherries lose considerable juice, which may take a few minutes, remove from heat. In a small bowl, mix the sugar and cornstarch together. Pour this mixture into the hot cherries and mix well. Add the almond extract, if desired, and mix. Return the mixture to the stove and cook over low heat until thickened, stirring frequently. Remove from the heat and let cool. If the filling is too thick, add a little water, too thin, add a little more cornstarch. Preheat the oven to 375 degrees F. Use your favorite pie dough recipe. Prepare your crust. Divide in half. Roll out each piece large enough to fit into an 8 to 9 -inch pan. Pour cooled cherry mixture into the crust. Dot with butter. Moisten edge of bottom crust. Place top crust on and flute the edge of the pie. Make a slit in the middle of the crust for steam to escape. Sprinkle with sugar. Bake for about 50 minutes. Remove from the oven and place on a rack to cool.

Algorithms are widely applicable, and, because they are stored in memory, save you the trouble of having to think. • What to do when you want a pizza. • What to do when you need to drive to an unfamiliar location. • Dealing with social situations?

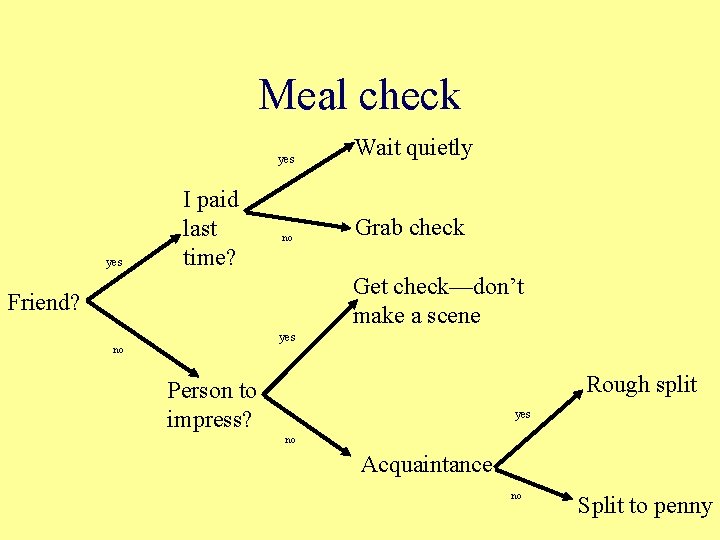
Meal check yes I paid last time? no Wait quietly Grab check Get check—don’t make a scene Friend? yes no Rough split Person to impress? yes no Acquaintance no Split to penny

Algorithms are great, but they are not applicable to all problems. You have to have some experience Must be a good definition of the starting point, the goal state, and methods available —i. e. , a well-defined problem. No algorithm for writing a novel.

Little knowledge What will you do when you have very little relevant knowledge? You have to fall back on operators that are very general-purpose, and will be more or less applicable to any situation.

Heuristics We do have heuristics we can use when we are in an unfamiliar problem solving situation. • • Brute force search Hill climbing Working backwards Means-ends analysis

Brute force search 2 down: “friend” A L You could sequentially go through the letters “a” “b” “c” until you found a suitable solution

Brute force--problem As the state space gets larger, you get combinatorial explosion

Hill climbing means looking ahead and selecting an operator that you judge will bring you closer to your goal; do not select an operator that will move you away from your goal.

Hill climbing works great for digging a hole

Hill climbing good for getting to the top of a hill. When would hill climbing not work?

I’m not on the highest peak--how will I get there?

If this dog wanted to sniff you, what would it do and what would it need to do? Hill climbing won’t work when you need to move away from the goal for a little while in order to eventually reach the goal.

Working backwards As the name suggests, working backwards means imagining being at the goal of the problem space and seeing if you can figure out a way to get to the initial state, or closer to it. http: //www. transience. com. au/pearl 3. html

Means ends analysis 1. Compare the current state to the goal state. If there is no difference between them, the problem is solved. 2. If there is a difference between the current state and the goal state, set as a goal to solve that difference. If there is more than one difference, set as a goal to solve the largest difference. 3. Select an operator that will solve the difference identified in step 2. 4. If the operator can be applied, apply it. If it cannot, set as a new goal to reach a state that would allow the application of the operator. 5. Return to step 1 with the new goal set in step 4.

Means ends analysis allows the setting of subgoals. That’s what’s missing from the other heuristics. Sometimes you must set a subgoal, which means temporarily moving away from the goal. It’s a combination of moving forwards & backwards.

Example Suppose I want to make Etouffee Step 1: Do I have Etouffee? No. Step 2: Goal: get Etouffee. Differences = knowledge, ingredients. Subgoal, get knowledge. Step 3: What has Etouffee knowledge? A cookbook. Step 4: Do I have a cookbook? No. Step 5: Set new subgoal: get cookbook, return step 1 Step 1: Do I have a cookbook? No. Step 2: Goal: get cookbook. Difference = distance to cookbook. Step 3: What reduces distance? A car Step 4: Can I use car? No. friend has keys. Step 5: Set new subgoal: get car keys. What would my solution be if I used hill-climbing?

Newell, Shaw & Simon The General Problem Solver was a computer program designed to solve problems using means ends analysis, and it was very effective. More important, it not only solved problems, the authors argued that it solved problems in ways similar to the ways humans solved problems.

Those four heuristics were for situations where you have little or no relevant knowledge. What happens if you have some relevant knowledge, but aren’t familiar with this particular problem?

You would think that some knowledge is better than none. The truth is that sometimes this knowledge helps and sometimes it doesn’t.

Knowledge can help. . . Knowledge can help when it allows you to recognize patterns based on past experience Experts recognize patterns, allowing them to limit the search space (e. g, they immediately perceive that the Queen is in trouble)

Knowledge can help. . . Experts also have automatized many of the rules. For example, they don’t need to use working memory capacity to count points in a bridge hand. 10 7 4 J 10 8 6 52 A 632 AKQ 96 32 W QJ 7 Q 10 8 N E S J AKQ 95 AK 64 974 8532 74 10 9 8 3 KJ 5

Prior knowledge can also impede

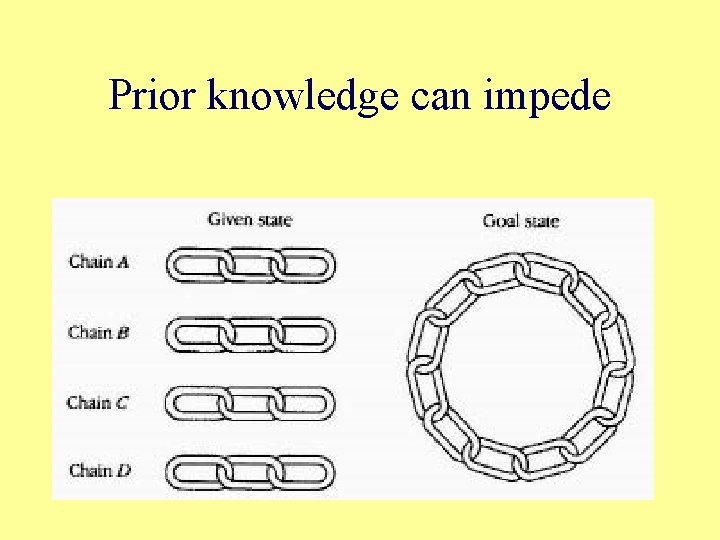
Prior knowledge can impede

Functional fixedness People fixate on the typical function of an object and fail to realize it can be used in an atypical way to solve a problem

Functional fixedness depends on prior knowledge—knowing the typical function. Pliers cut things, don’t serve as weight Cutting a link allows joining of the attached length of chain

Other prior knowledge You can be fixated not only on the function of an object, but also on the procedures used to solve a problem--try to solve a problem as you have before, even if the procedures are no longer appropriate.

Luchins’s water jars Problem number Jug A Jug B Jug C Required Amount 1 18 43 10 5 2 21 127 33 40 3 14 163 25 99 7 23 49 3 20 8 15 39 3 18 9 28 76 3 25 Formula B -A- 2 C works, but not for 9, and 7 and 8 have easier solutions

You should bear in mind that being an expert almost always helps you. The problem arises where it looks like knowledge you have will be applicable, but it actually leads you down the wrong solution path.

What makes an expert? Surprising upshot: it doesn’t seem to be that they are better at choosing operators. Rather, they seem to be better at restricting the search space. They can do that by recognizing familiar patterns.

Chess experts may have as many as 50, 000 board positions in memory. When a chess master plays many people simultaneously (at an exhibition) his play is not much worse than when he’s at a tournament, even though he has much less time per move. This indicates that the amount of time spent considering moves is not so important.

This has led to the more general hypothesis that experts are not so different than novices in terms of how they select operators, but are different in terms of how they think of the search space.

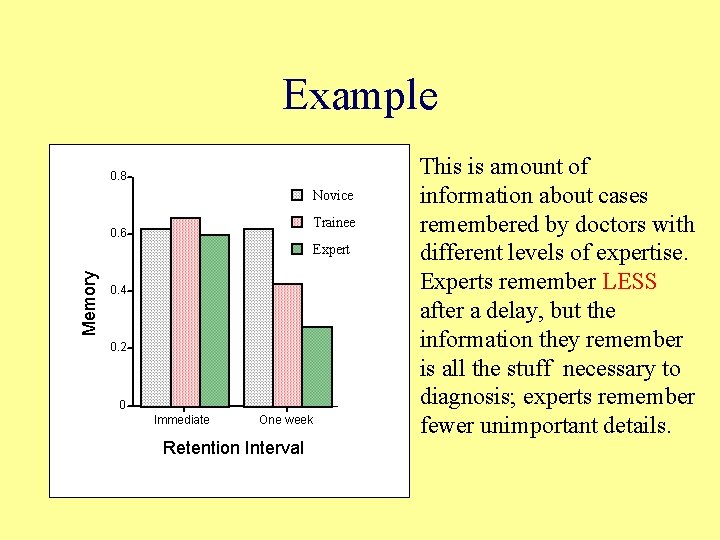
Example 0. 8 Novice Trainee 0. 6 Memory Expert 0. 4 0. 2 0 Immediate One week Retention Interval This is amount of information about cases remembered by doctors with different levels of expertise. Experts remember LESS after a delay, but the information they remember is all the stuff necessary to diagnosis; experts remember fewer unimportant details.

How do you get to be an expert? Practice like crazy for 10 years

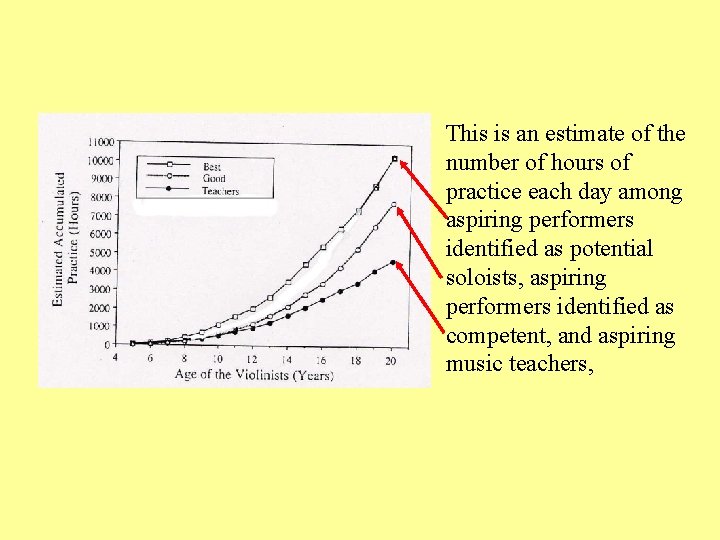
This is an estimate of the number of hours of practice each day among aspiring performers identified as potential soloists, aspiring performers identified as competent, and aspiring music teachers,

Broad summary • If you have no clue about a problem, you apply a heuristic • If some elements of a problem seem familiar, it may help, but if the part that is familiar leads you to a solution that is ineffective, it will hurt. • Experts probably don’t solve problems differently than you, they just know more than you do.