Problem Solving Arithmetic Progression and Geometric Progression Last

Problem Solving Arithmetic Progression and Geometric Progression Last Updated: October 11, 2005

Review -- Arithmetic nth term Jeff Bivin -- LZHS Sum of n terms

Review -- Geometric nth term an = a 1 Jeff Bivin -- LZHS (n-1) ·r Sum of n terms

Example 1 The sum of the first n terms of a progression is given by Sn = n 2 + 3 n. Find, in terms of n the nth term. Sn = n 2 + 3 n Sn-1 = (n-1)2 + 3(n-1) = n 2 – 2 n + 1 + 3 n – 3 = n 2 + n – 2 Tn = Sn – 1 = n 2 + 3 n – (n 2 + n – 2) = 2 n + 2 Jeff Bivin -- LZHS

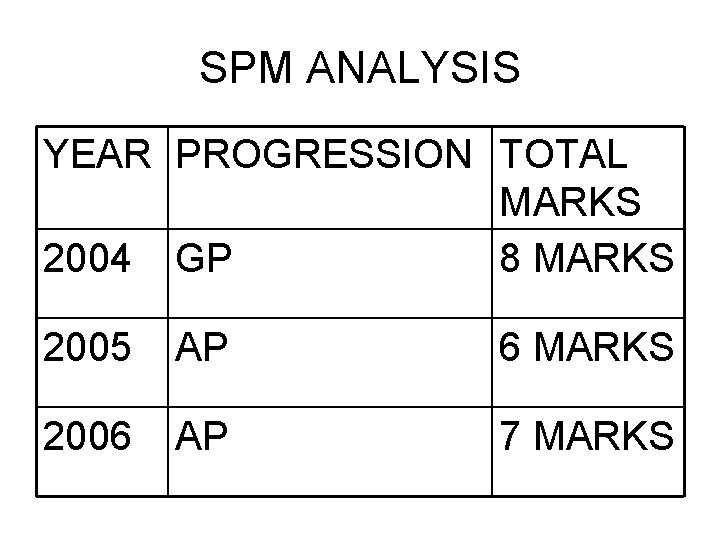
SPM ANALYSIS YEAR PROGRESSION TOTAL MARKS 2004 GP 8 MARKS 2005 AP 6 MARKS 2006 AP 7 MARKS

Year 2004, SPM PAPER 2 y cm x cm The diagram shows the arrangement of the first 3 of an infinite series of similar triangles. The first triangle has a base of x cm and a height of y cm. The measurements of the base and the height of each subsequent triangle are half of the measurement of its previous one. (a) Show that the areas of the triangles form a geometric progression and state the common ratio. [3 marks] (b) Given that x = 80 and y = 40 [5 marks] (i) determine which triangle has an area of 6. 25 cm 2 (ii) find the sum to infinity of the areas in cm 2 of the triangles Jeff Bivin -- LZHS

SOLUTION (a) Area of 1 st triangle: A 1 = Area of 2 nd triangle: A 2= Area of 3 rd triangle: A 3 = The area of triangles form a GP with common ratio Jeff Bivin -- LZHS

SOLUTION (b)(i) Area of nth triangle: An = A 1 r n – 1 6. 25 = The fifth triangle has area of 6. 25 cm 2 Jeff Bivin -- LZHS

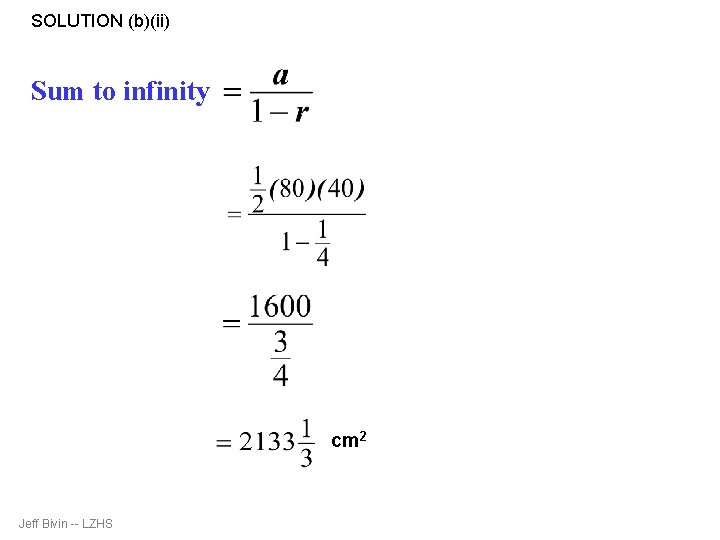
SOLUTION (b)(ii) Sum to infinity cm 2 Jeff Bivin -- LZHS

Year 2005, SPM PAPER 2 Diagram above shows part of an arrangement of bricks of equal size. The number of bricks in the lowest row is 100. For each of the other rows, the number of bricks is 2 less than in the row below. The height of each brick is 6 cm. Ali builds a wall by arranging bricks in this way. The number of bricks in the highest row is 4. Calculate (a) The height, in cm, of the wall [3 marks] (b) The total price of the bricks used if the price of of one brick is 40 sen. [3 marks] Jeff Bivin -- LZHS

Year 2005, SPM PAPER 2 The arrangement of bricks is in arithmetic progression: 100, 98, 96, 94, 92, …. 8, 6, 4. a = 100, d = -2 Let Tn = 4 100 + (n – 1)(-2) = 4 96 = 2(n – 1) 48 = n - 1 n = 49 (a) The height of the wall = 49 6 = 294 cm. (b) Total bricks used = The total price of bricks used = 2, 548 0. 40 = RM 1, 019. 20 Jeff Bivin -- LZHS

Year 2006, SPM PAPER 2 Two companies, Delta and Omega, start to sell cars at the same time. (a) Delta sells k cars in the first month and its sales increase constantly by m cars every subsequent month. It sells 240 cars in the 8 th month and the total sales for the first 10 months are 1900 cars. Find the value of k and of m. [5 marks] (a) Omega sells 80 cars in the first month and its sales increase constantly by 22 cars every subsequent month. If both companies sell the same number of cars in the nth month, find the value of n. [2 marks] Jeff Bivin -- LZHS

k, k+m, k+2 m, k+ 3 m, k+4 m, …. . 240 = k + 7 m……. . (1) 1900 = 5(2 k+9 m) 380 = 2 k + 9 m……. (2) (1) 2 – (2): 480 – 380 = 14 m – 9 m 100 = 5 m m = 20 Substitute m = 20 into (1): 240 = k + 7(20) k = 240 – 140 k = 100

Delta: 100, 120, 140, 160, 180, …. Tn = 100 + 20(n – 1) Omega: 80, 102, 124, 146, 168, … Tn = 80 + 22(n – 1) 100 + 20(n – 1) = 80 + 22(n – 1) 100 + 20 n – 20 = 80 + 22 n – 22 80 + 20 n = 58 + 22 n 22 = 2 n n = 11