PROBLEM SOLVING AND DIMENSIONAL ANALYSIS VERIFICATION Dimensional Analysis

PROBLEM SOLVING AND DIMENSIONAL ANALYSIS VERIFICATION Dimensional Analysis and Significant Digits The RULE OF ZERO! LEARN THE RULES

PROBLEM SOLVING AND DIMENSIONAL ANALYSIS Dimensional Analysis VERIFICATION Conversions require one to get rid of all units they are not interested in by ensuring they appear both above and below the line at some point in order to cancel out. Multiply what is on either size Divide what is above and below

PROBLEM SOLVING AND DIMENSIONAL ANALYSIS VERIFICATION I made a mistake in negotiating my contract. I agreed to my vacation time in second for next year. I agreed to 1, 296, 000 seconds. How many days of vacation did I negotiate? =

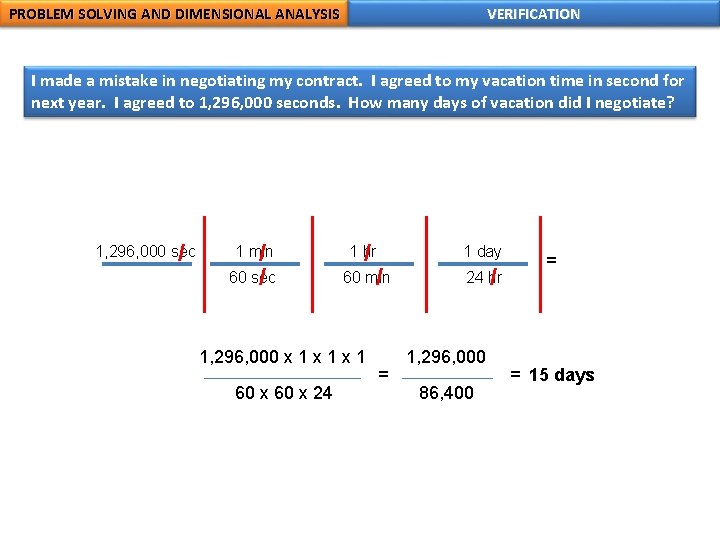
PROBLEM SOLVING AND DIMENSIONAL ANALYSIS VERIFICATION I made a mistake in negotiating my contract. I agreed to my vacation time in second for next year. I agreed to 1, 296, 000 seconds. How many days of vacation did I negotiate? 1, 296, 000 sec / 1 min / 60 sec / 1 hr / 60 min / 1, 296, 000 x 1 x 1 60 x 24 1 day = 24 hr / 1, 296, 000 86, 400 = = 15 days

PROBLEM SOLVING AND DIMENSIONAL ANALYSIS VERIFICATION Charles Wynder can run the “Football 40”, a 40 yard dash race, in 4. 5 seconds. When asked what this would register on a car’s speedometer in miles per hour he did not know. We can calculate this and determine just how fast is Charles in miles per hour. =

PROBLEM SOLVING AND DIMENSIONAL ANALYSIS VERIFICATION Charles Wynder can run the “Football 40”, a 40 yard dash race, in 4. 5 seconds. When asked what this would register on a car’s speedometer in miles per hour he did not know. We can calculate this and determine just how fast is Charles in miles per hour. 40 yds / 4. 5 sec / 60 sec / 1 min / 3 ft/ 60 min / 4. 5 x 1 x 1 x 5, 280 = 432, 000 23, 760 = 5, 280 ft/ 1 yd / 1 hr 40 x 60 x 3 x 1 1 mile = 18. 18 Miles Hour

PROBLEM SOLVING AND DIMENSIONAL ANALYSIS VERIFICATION My American Made car gets 23 miles per gallon of gas. When I chose to sell it to Mr. Heaton, he asked how many kilometers per liter could he expect to get when driving. What am I converting? What special conversions do I need to know? 5, 280 feet in 1 mile 3. 785 liters in 1 gallon (Use 3. 8 liters) 2. 54 cm in 1 inch 100 cm in 1 meter 1000 m in 1 km =

PROBLEM SOLVING AND DIMENSIONAL ANALYSIS Significant Figures VERIFICATION How to Determine Rules for Significant Figures 1. Non-zero integers 2. Zeros a. Leading zeros (those appearing before non-zero integers) never count b. Captive zeros (those appearing between nonzero integers) always count c. Trailing zeros (those at the right end of non-zero integers) count only when there is a decimal point • 100 has 1 sig fig • 100. has 3 sig figs 3. Exact Numbers a. Counted, but not measured b. Definitions (1 inch = 2. 54 cm) Rules for Rounding 1. If the digit to be removed a. <5 the number remains the same (e. g. , 1. 33 rounds to 1. 3) b. =/> 5 the number increase by 1 (e. g. , 1. 35 rounds to 1. 4) 2. In a series of calculations a. Carry the extra digits to the end b. Round the final answer Rules for Significant Figures in Calculations 1. Multiplication and Division - Limited to the smallest number of sig figs in the numbers used in the operation (e. g. , 4. 56 x 1. 4 = 6. 384 rounded to 2 sig figs because of 1. 4, so the answer is 6. 4) 2. Addition and Subtraction – The smallest number of decimal places (e. g. , 12. 11 + 18. 0 + 1. 013 = 31. 123 rounded to 3 sig figs because 18. 0 has only 1 decimal place, so the answer is 31. 1)

PROBLEM SOLVING AND DIMENSIONAL ANALYSIS VERIFICATION Give the number of significant figures for the following: 1. A sample of OJ contains 0. 0108 g of Vitamin C. ______ 2. A hair weighed in a crime lab has a mass of 0. 0050060 g. ______ 3. The distance between two points is 5. 030 x 103 ft. ______ 4. 100 runners began the race, but only 60 completed the course. ______ Without performing the calculation, predict the number of sig figs there in the final answer. Sum of Difference of Product of Cost of 5. 19 1. 9 0. 842 1081 – 7. 25 2. 3 x 3. 14 3 Boxes of candy at $2. 50 per box 2 Calculations using significant figures : 5. 18 x 0. 0208 = 116. 83 – 0. 33 = (3. 60 x 10 -3) x (8. 123) ÷ 4. 3 = 1. 33 x 2. 8 + 8. 41 =

How to Determine Rules for Significant Figures 1. Non-zero integers 2. Zeros a. Leading zeros (those appearing before non-zero integers) never count b. Captive zeros (those appearing between nonzero integers) always count c. Trailing zeros (those at the right end of non-zero integers) count only when there is a decimal point • 100 has 1 sig fig • 100. has 3 sig figs 3. Exact Numbers a. Counted, but not measured b. Definitions (1 inch = 2. 54 cm) Rules for Rounding 1. If the digit to be removed a. <5 the number remains the same (e. g. , 1. 33 rounds to 1. 3) b. =/> 5 the number increase by 1 (e. g. , 1. 35 rounds to 1. 4) 2. In a series of calculations a. Carry the extra digits to the end b. Round the final answer Rules for Significant Figures in Calculations 1. Multiplication and Division - Limited to the smallest number of sig figs in the numbers used in the operation (e. g. , 4. 56 x 1. 4 = 6. 384 rounded to 2 sig figs because of 1. 4, so the answer is 6. 4) 2. Addition and Subtraction – The smallest number of decimal places (e. g. , 12. 11 + 18. 0 + 1. 013 = 31. 123 rounded to 3 sig figs because 18. 0 has only 1 decimal place, so the answer is 31. 1)

Cómo determinar Reglas para cifras significativas 1. 2. 3. Números enteros de distinto de cero Ceros a) (Los que aparecen antes de números enteros distintos de cero) de los ceros no cuentan b) Cautivo (los que aparecen entre números enteros distintos de cero) ceros siempre contar c) Ceros finales (ésos a la derecha de cero enteros) cuenta sólo cuando hay un punto decimal • 100 tiene 1 sig Fig. • 100. tiene 3 higos de sig Números exactos a) Contado, pero no medido b) Definiciones (1 pulgada = 2, 54 cm) Reglas de redondeo 1. Si el dígito a ser eliminado a) < 5 el número sigue siendo el mismo (por ejemplo, 1, 33 rondas a 1. 3) b) = / > 5 el número de aumento por 1 (por ejemplo, 1, 35 rondas a 1. 4) 2. En una serie de cálculos a) Llevar los dígitos adicionales hasta el final b) Alrededor de la respuesta final Reglas para cifras significativas en cálculos 1. Multiplicación y división - limitada a la menor cantidad de higos de sig en los números utilizados en la operación (por ejemplo, 4. 56 x 1. 4 = 6. 384 redondeado a 2 higos de sig por 1. 4, entonces la respuesta es 6. 4) 2. Suma y resta, el número más pequeño de decimales (por ejemplo, 12. 11 + 18. 0 + 1. 013 = 31. 123 redondeado a 3 higos de sig porque 18. 0 tiene sólo 1 lugar decimal, entonces la respuesta es 31. 1)