Problem Posing The Invention of Great Problems Dr

Problem Posing: The Invention of Great Problems Dr. Betty K. Wood & Dr. James M. Fetterly bkwood@ualr. edu jfetterly@uca. edu Handouts for this session can be found on the AMLE 2015 app

Session Evaluation Let us know what you thought of this session. Complete an evaluation electronically on the conference app, or complete the paper evaluation located in the back of the program book. CEU Code Earn Continuing Education Units (CEU) to maintain your teaching certification. Write down the CEU Code for every session you attend on the CEU card located in the back of the program book. CEU Code: KC-25

Arkansas i. Tunes U Understanding and Developing Fractions Alternative Algorithms Problem Solving the Square-iest Situations

Great Problems • Don’t have to have grand beginnings • Are individually problematic • Begin with intrigue • Can be extended • Continue with curiosity • Can be addressed in multiple ways • Can be understood in various manners • Possess meaningful structure • Are related to other concepts

Four Consecutive Numbers Some people say that to add four consecutive numbers you add the first and the last numbers and multiply by 2. What can you find out about that?

Six Consecutive Numbers Some people say that to add six consecutive numbers you add the first and the last numbers and multiply by X.

Eight Consecutive Numbers Some people say that to add eight consecutive numbers you add the first and the last numbers and multiply by X.

Your problem may be modest, but if it challenges your curiosity and brings into play your inventive faculties, and if you solve it by your own means, you may experience the tension and enjoy the triumph of discovery. George Polya

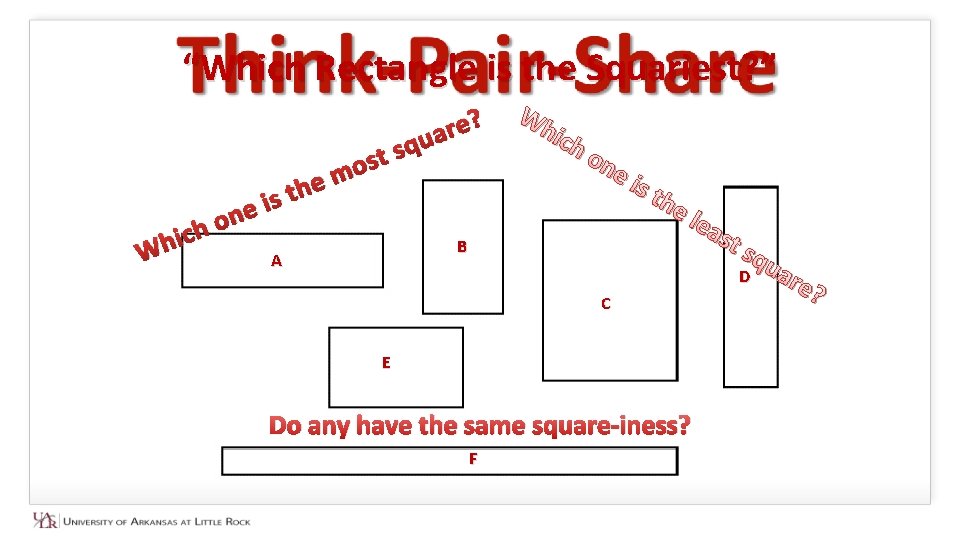
“Which Rectangle is the Squariest? ” W h c i h one e h t is s o m u q s t ? are Wh ich on B A ei st he lea st squ D C E Do any have the same square-iness? F are ?

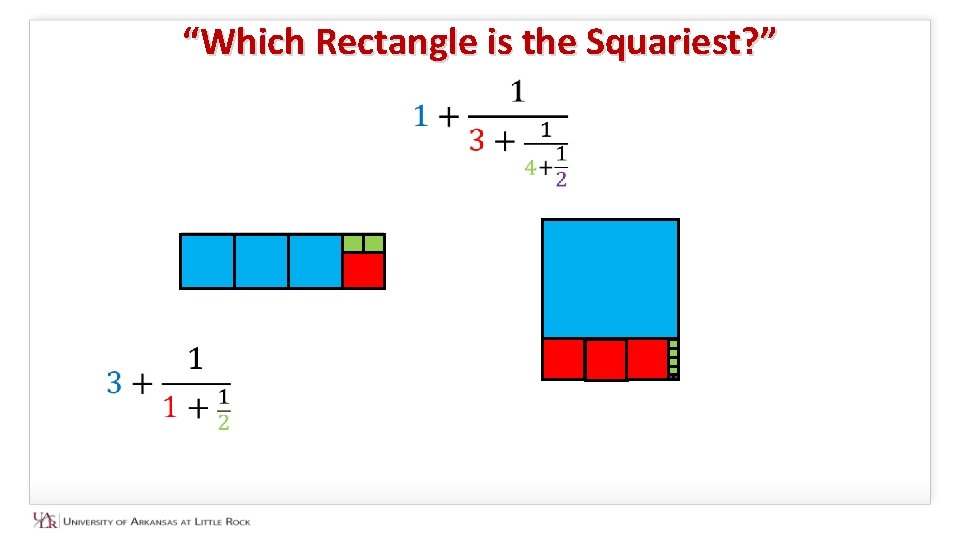
“Which Rectangle is the Squariest? ” A C

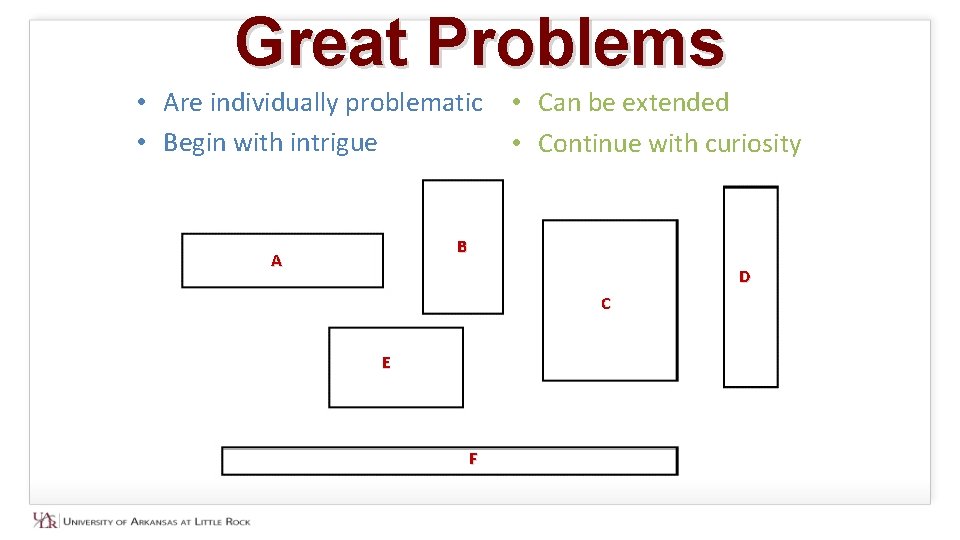
Great Problems • Are individually problematic • Can be extended • Begin with intrigue • Continue with curiosity B A D C E F

Beauty in mathematics is seeing the truth without effort. George Polya

Start And Jump Numbers: Searching For Patterns • You will need to make a list of numbers that begin with a “start number” and increase by a fixed amount we will call the “jump number. ” First try 3 as the start number and 5 as the jump number. Write the start number at the top of your list, then 8, 13, and so on, “jumping” by 5 each time until your list extends to about 130.

Start And Jump Numbers: Searching For Patterns • Your task is to examine this list of numbers and find as many patterns as you possibly can. Share your ideas with the group, and write down every pattern you agree really is a pattern.

Great Problems • Don’t have to have grand beginnings • Are individually problematic • Begin with intrigue • Can be extended • Continue with curiosity • Can be addressed in multiple ways • Can be understood in various ways • Possess meaningful structure • Are related to other concepts

If you can’t solve a problem, then there is an easier problem you can solve: find it. George Polya

Try Time 3, 4, 5, 6, 12, & 13 Arrange the following whole numbers (3, 4, 5, 6, 12, & 13) in a row without repetition so that the sum of any two adjoining numbers is a perfect square. Find the sum of the two middle numbers.

P airs that S quare 3, 4, 5, 6, 12, & 13 Problem Solving Strategy: 3 + 4 = 7 Order and Organize Data 3 + 5 = 8 3 + 6 = 9 3 + 12 = 15 3 + 13 = 16

P airs that S quare 3, 4, 5, 6, 12, & 13 3 + 4 = 7 3 + 5 = 8 3 + 6 = 9 3 + 12 = 15 3 + 13 = 16

P airs that S quare 3, 4, 5, 6, 12, & 13 4 + 5 = 9 4 + 6 = 10 4 + 12 = 16 4 + 13 = 17

P airs that S quare 3, 4, 5, 6, 12, & 13 5 + 6 = 11 5 + 12 = 17 5 + 13 = 18

P airs that S quare 3, 4, 5, 6, 12, & 13 6 + 12 = 18 6 + 13 = 19

P airs that S quare 3, 4, 5, 6, 12, & 13 12 + 13 = 25

P airs that S quare 3, 4, 5, 6, 12, & 13 3 + 6 = 9 3 + 13 = 16 4 + 5 = 9 4 + 12 = 16 12 + 13 = 25 Observations & Reflections

P airs that S quare 5, 4, 12, 13, 3, 6 3 + 6 = 9 3 + 13 = 16 4 + 5 = 9 4 + 12 = 16 12 + 13 = 25

Certainly, let us learn proving, but also let us learn guessing. George Polya

Try Time Find the least positive integer T so that the product of 45 and T is a perfect square.

Brown, S. , & Walter, M. (2005). The art of problem posing (3 rd Ed). Hillsdale, NJ: Lawrence Erlbaum. “What-If-Not” 54 B = N² 72 ÷ C = N² 63 D = N³ 81 ÷ E = N³ 36 F = N 4

Arkansas i. Tunes U Understanding and Developing Fractions Alternative Algorithms Problem Solving the Square-iest Situations

Author Unknown Good mathematics is NOT how many answers you know … but how you behave when you don’t know.

Lauren Resnick [Students] who are successful at making sense of mathematics are those who believe that mathematics make sense.

Student Responses N = s + s+ s+ s + 4 N = 4(s + 1) N = 4 s + 4 N = 2 s +2(s + 2) N = 8 + 4(s-1) N = (s + 2)2 – s 2 N = s 2 - (s-2)² + 8