Probing the neutral intergalactic medium during cosmic reionization

Probing the neutral intergalactic medium during cosmic reionization using the 21 cm line of hydrogen KIAA-PKU Summer School, Beijing, China Chris Carilli, NRAO, August 10, 2007 § Introduction: What is Cosmic Reionization? § Current constraints on the IGM neutral fraction with cosmic epoch § Neutral Intergalactic Medium (IGM) – HI 21 cm signals § Low frequency telescopes and observational challenges

References Reionization and HI 21 cm studies of the neutral IGM § “Observational constraints on cosmic reionization, ” Fan, Carilli, Keating 2006, ARAA, 44, 415 §“Cosmology at low frequencies: the 21 cm transition and the high redshift universe, ” Furlanetto, Oh, Briggs 2006, Phys. Rep. , 433, 181 Early structure formation and first light § “The first sources of light and the reionization of the universe, ” Barkana & Loeb 2002, Phys. Rep. , 349, 125 § “The reionization of the universe by the first stars and quasars, ” Loeb & Barkana 2002, ARAA, 39, 19 § “Observations of the high redshift universe, ” Ellis 2007, Saas-Fe advanced course 36

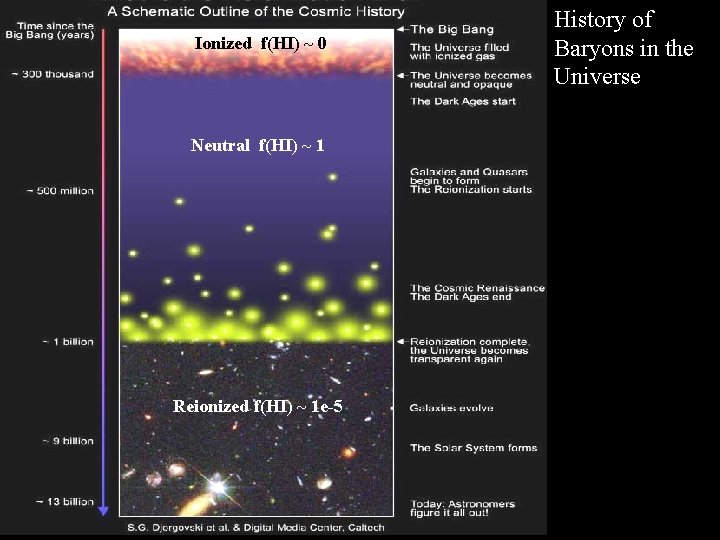
Ionized f(HI) ~ 0 Neutral f(HI) ~ 1 Reionized f(HI) ~ 1 e-5 History of Baryons in the Universe

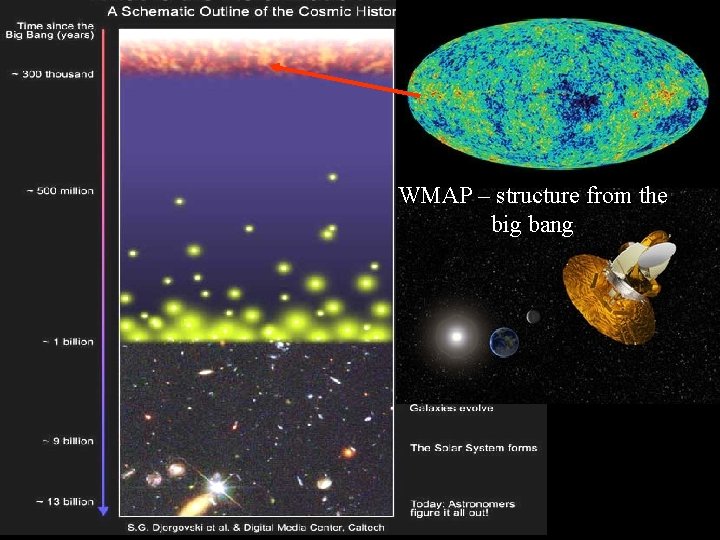
Chris Carilli (NRAO) Berlin June 29, 2005 WMAP – structure from the big bang

Hubble Space Telescope Realm of the Galaxies

Dark Ages Twilight Zone Epoch of Reionization • Last phase of cosmic evolution to be tested • Bench-mark in cosmic structure formation indicating the first luminous structures

Dark Ages Twilight Zone Epoch of Reionization • Epoch? • Process? • Sources?

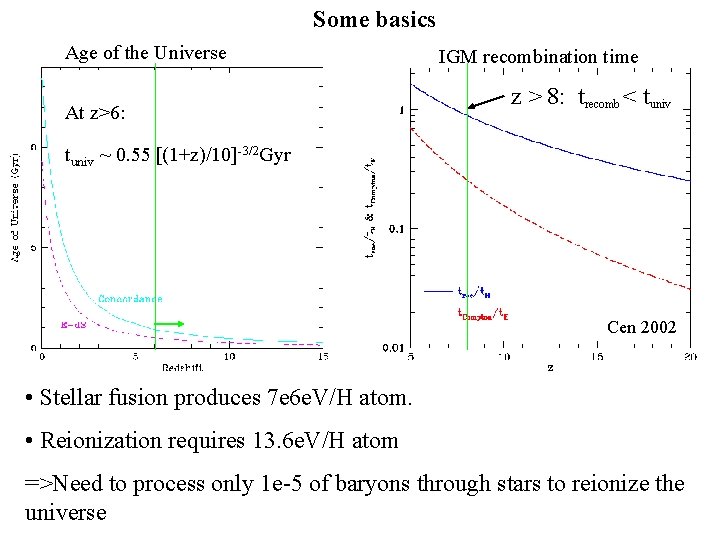
Some basics Age of the Universe At z>6: IGM recombination time z > 8: trecomb < tuniv ~ 0. 55 [(1+z)/10]-3/2 Gyr Cen 2002 • Stellar fusion produces 7 e 6 e. V/H atom. • Reionization requires 13. 6 e. V/H atom =>Need to process only 1 e-5 of baryons through stars to reionize the universe

Reionization: the movie Gnedin 03 8 Mpc comoving

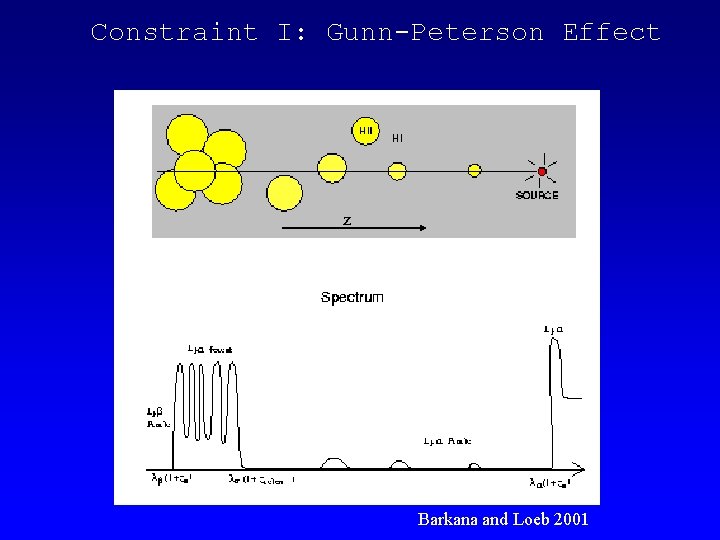
Constraint I: Gunn-Peterson Effect z Barkana and Loeb 2001

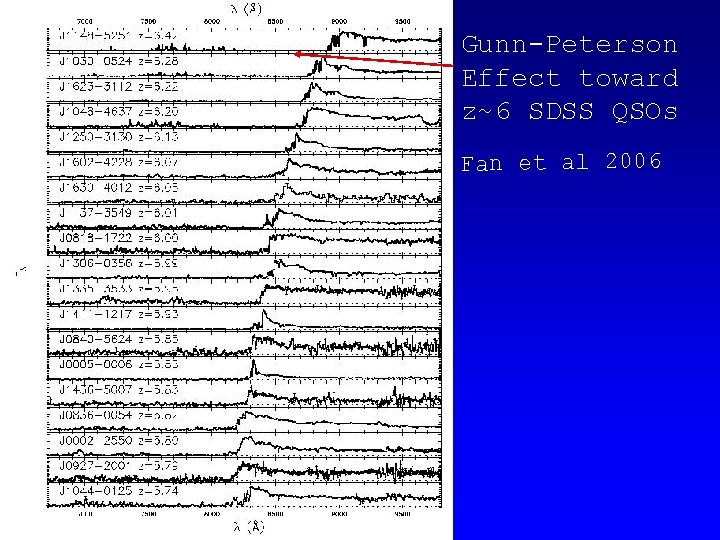
Gunn-Peterson Effect toward z~6 SDSS QSOs Fan et al 2006

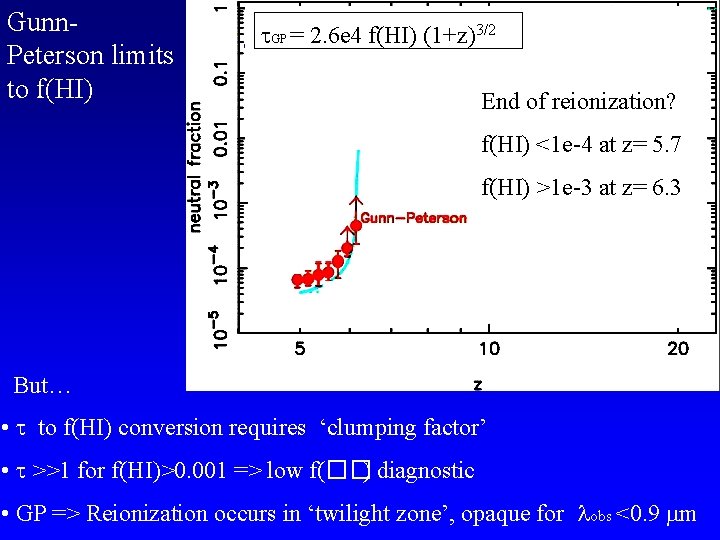
Gunn. Peterson limits to f(HI) GP = 2. 6 e 4 f(HI) (1+z)3/2 End of reionization? f(HI) <1 e-4 at z= 5. 7 f(HI) >1 e-3 at z= 6. 3 But… • to f(HI) conversion requires ‘clumping factor’ • >>1 for f(HI)>0. 001 => low f(��) diagnostic • GP => Reionization occurs in ‘twilight zone’, opaque for obs <0. 9 m

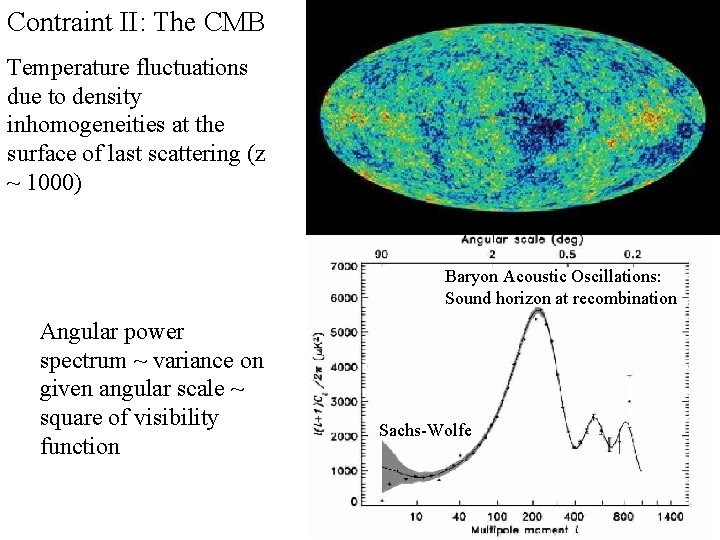
Contraint II: The CMB Temperature fluctuations due to density inhomogeneities at the surface of last scattering (z ~ 1000) Baryon Acoustic Oscillations: Sound horizon at recombination Angular power spectrum ~ variance on given angular scale ~ square of visibility function Sachs-Wolfe

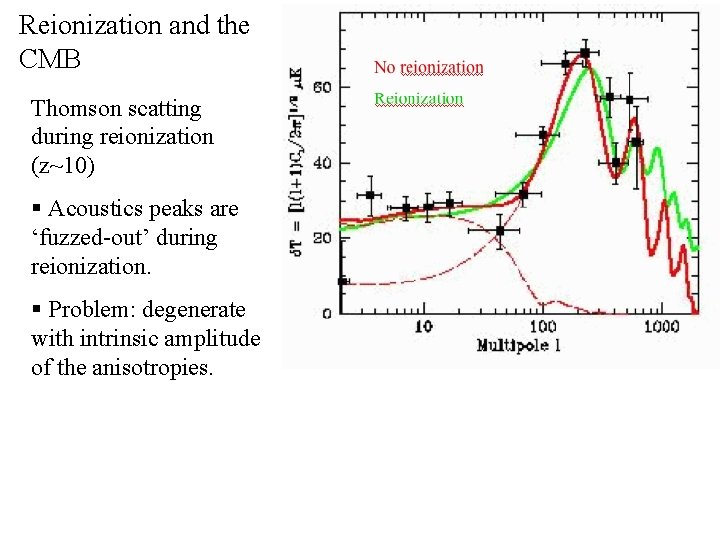
Reionization and the CMB Thomson scatting during reionization (z~10) § Acoustics peaks are ‘fuzzed-out’ during reionization. § Problem: degenerate with intrinsic amplitude of the anisotropies.

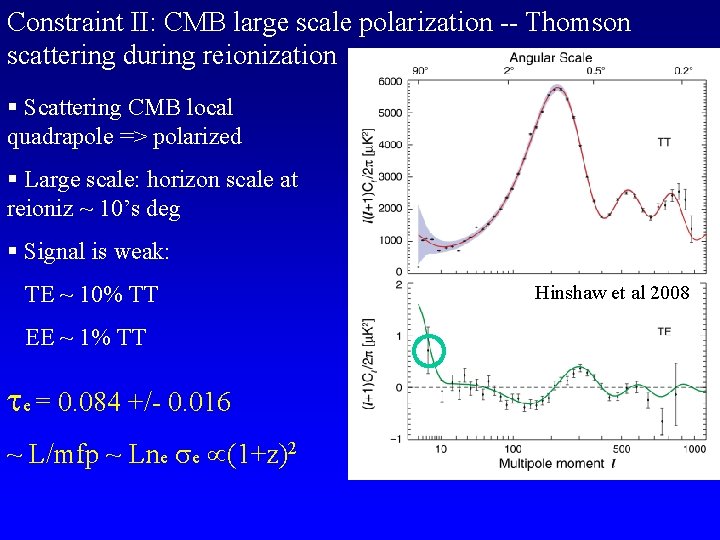
Constraint II: CMB large scale polarization -- Thomson scattering during reionization § Scattering CMB local quadrapole => polarized § Large scale: horizon scale at reioniz ~ 10’s deg § Signal is weak: TE ~ 10% TT EE ~ 1% TT e = 0. 084 +/- 0. 016 ~ L/mfp ~ Lne e (1+z)2 Hinshaw et al 2008

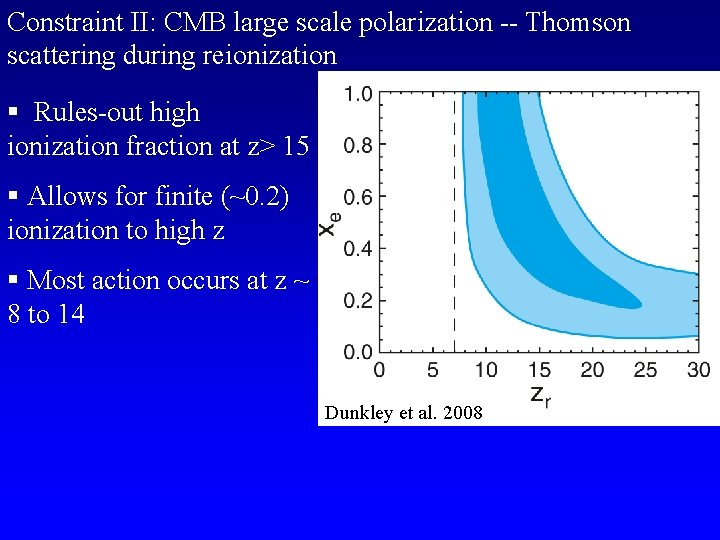
Constraint II: CMB large scale polarization -- Thomson scattering during reionization § Rules-out high ionization fraction at z> 15 § Allows for finite (~0. 2) ionization to high z § Most action occurs at z ~ 8 to 14 Dunkley et al. 2008

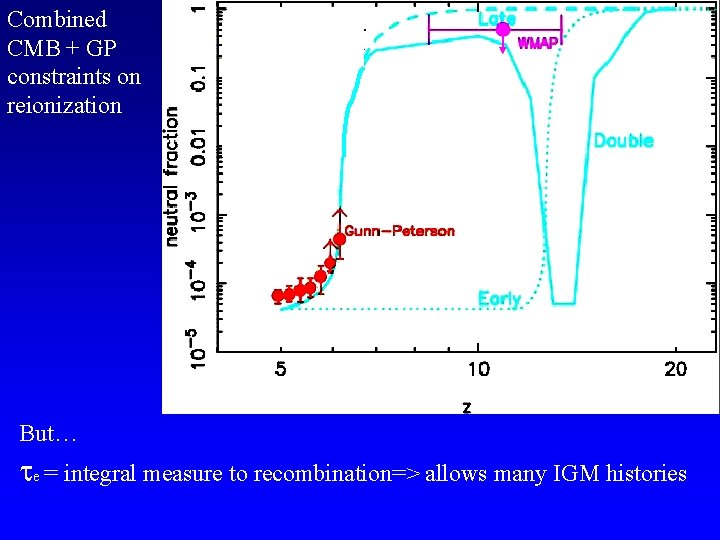
Combined CMB + GP constraints on reionization But… e = integral measure to recombination=> allows many IGM histories

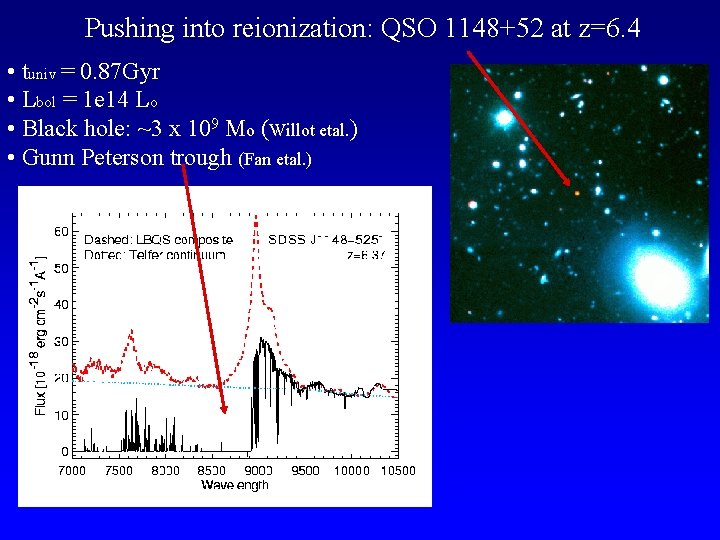
Pushing into reionization: QSO 1148+52 at z=6. 4 • tuniv = 0. 87 Gyr • Lbol = 1 e 14 Lo • Black hole: ~3 x 109 Mo (Willot etal. ) • Gunn Peterson trough (Fan etal. )

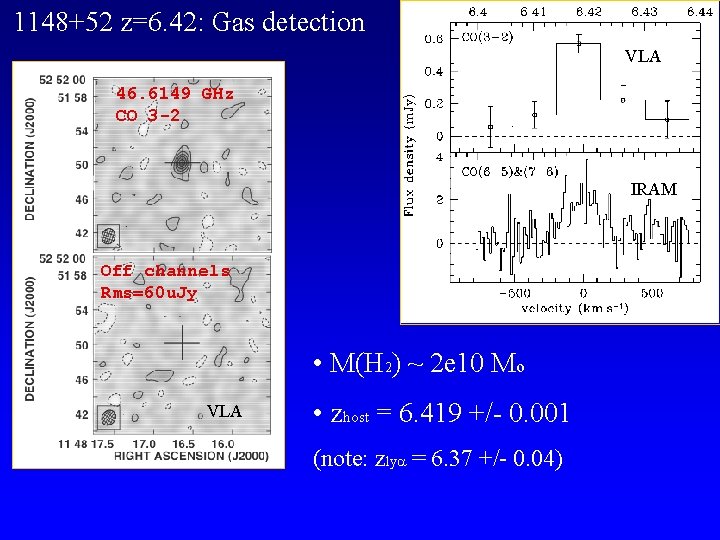
1148+52 z=6. 42: Gas detection VLA 46. 6149 GHz CO 3 -2 IRAM Off channels Rms=60 u. Jy • M(H 2) ~ 2 e 10 Mo VLA • zhost = 6. 419 +/- 0. 001 (note: zly = 6. 37 +/- 0. 04)

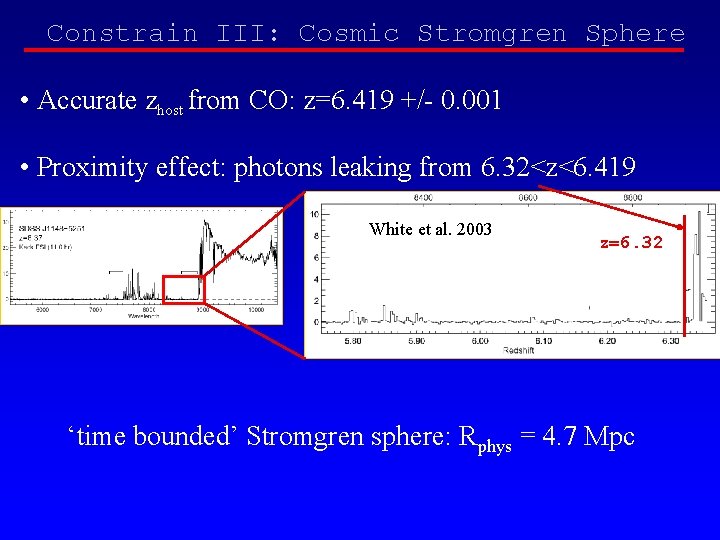
Constrain III: Cosmic Stromgren Sphere • Accurate zhost from CO: z=6. 419 +/- 0. 001 • Proximity effect: photons leaking from 6. 32<z<6. 419 White et al. 2003 z=6. 32 ‘time bounded’ Stromgren sphere: Rphys = 4. 7 Mpc

‘time bounded’ Stromgren sphere: R = 4. 7 Mpc # ionizing photons = # atoms in volume Luv • tqso = 4/3 R 3 • <n. HI> => tqso = 1 e 5 R 3 f(HI)~ 1 e 7 yrs f(HI) ~ 1 (tqso/1 e 7 yr) or Loeb & Rybicki 2000

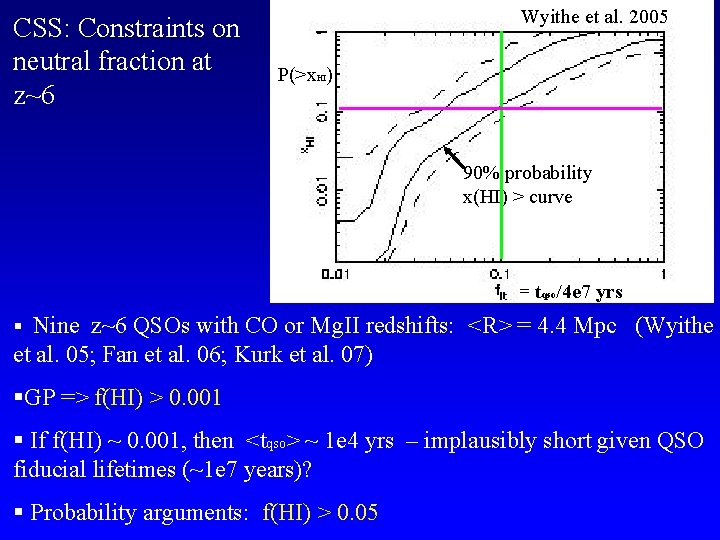
CSS: Constraints on neutral fraction at z~6 Wyithe et al. 2005 P(>x. HI) 90% probability x(HI) > curve = tqso/4 e 7 yrs § Nine z~6 QSOs with CO or Mg. II redshifts: <R> = 4. 4 Mpc (Wyithe et al. 05; Fan et al. 06; Kurk et al. 07) §GP => f(HI) > 0. 001 § If f(HI) ~ 0. 001, then <tqso> ~ 1 e 4 yrs – implausibly short given QSO fiducial lifetimes (~1 e 7 years)? § Probability arguments: f(HI) > 0. 05

Difficulties for Cosmic Stromgren Spheres (Lidz + 07, Maselli + 07) § Requires sensitive spectra in difficult near-IR band § Sensitive to R: f(HI) R^-3 § Clumpy IGM => ragged edges § Pre-QSO reionization due to star forming galaxies, early AGN activity

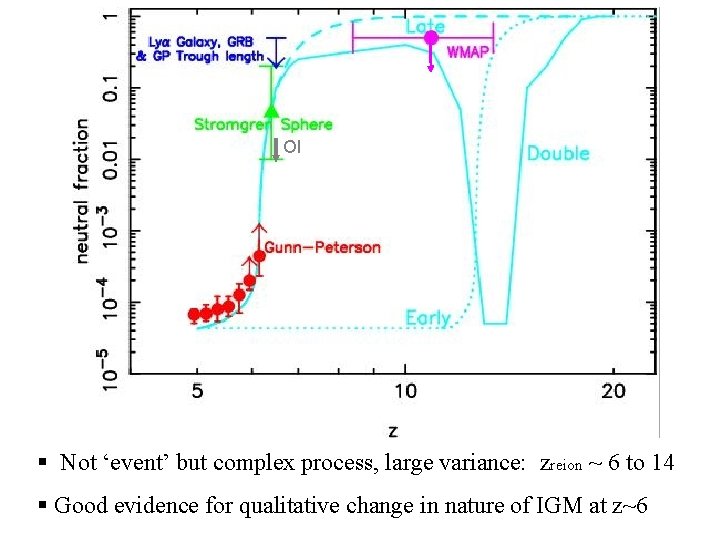
OI § Not ‘event’ but complex process, large variance: zreion ~ 6 to 14 § Good evidence for qualitative change in nature of IGM at z~6 ESO

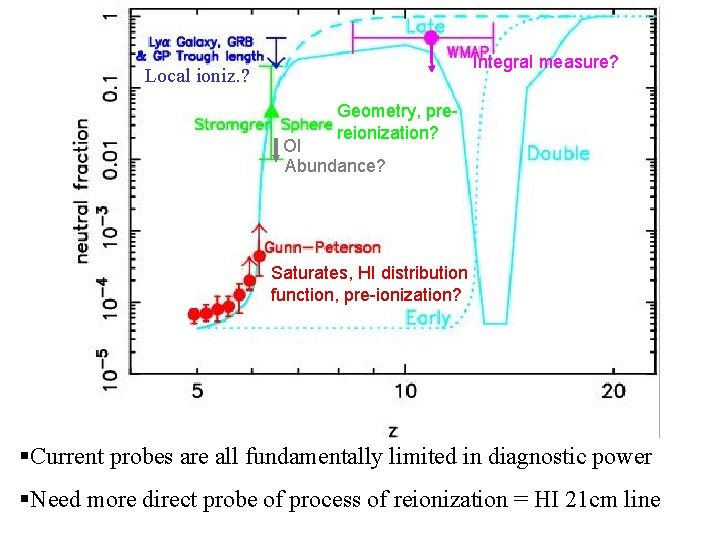
Integral measure? Local ioniz. ? Local ionization? Geometry, prereionization? OI Abundance? Saturates, HI distribution function, pre-ionization? §Current probes are all fundamentally limited in diagnostic power §Need more direct probe of process of reionization = HI 21 cm line

Low frequency radio astronomy: Most direct probe of the neutral IGM during, and prior to, cosmic reionization, using the redshifted HI 21 cm line: z>6 => 100 – 200 MHz Square Kilometer Array

Advantages to the HI 21 cm line 1. Spectral line signal => full three dimensional (3 D) diagnostic of structure formation. 2. Direct probe of IGM = dominant component of baryons during reinization/dark ages 3. Hyperfine transition = forbidden (weak) => avoid saturation (cf. Ly ), can study the full redshift range of reionization. Diagnostics: 1. When: direct measure of epoch of reionization 2. Process: Inside-out vs. outside-in reionization 3. Sources: Xrays vs. UV vs. shocks 4. Feedback due to galaxy/AGN formation 5. Exotic mechanisms: Very high z particle decay

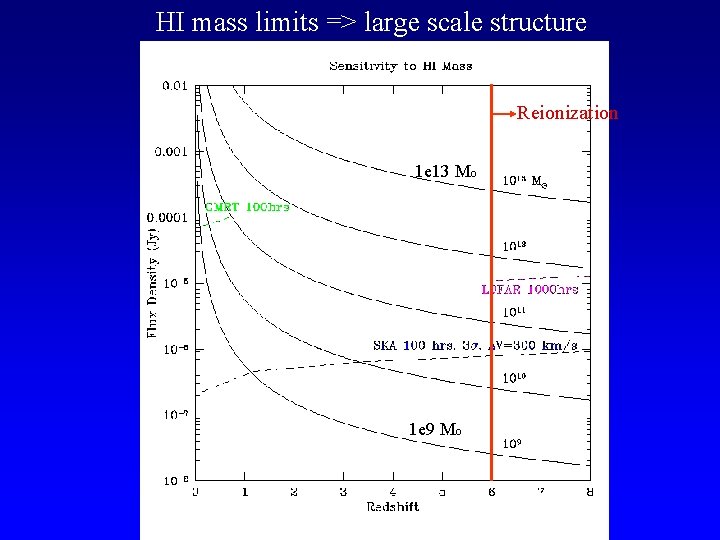
HI mass limits => large scale structure Reionization 1 e 13 Mo 1 e 9 Mo

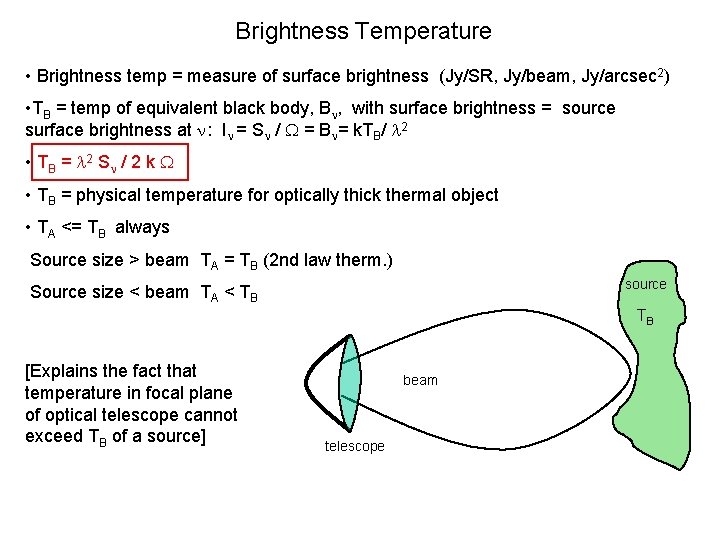
Brightness Temperature • Brightness temp = measure of surface brightness (Jy/SR, Jy/beam, Jy/arcsec 2) • TB = temp of equivalent black body, B , with surface brightness = source surface brightness at : I = S / = B = k. TB/ 2 • TB = 2 S / 2 k • TB = physical temperature for optically thick thermal object • TA <= TB always Source size > beam TA = TB (2 nd law therm. ) source Source size < beam TA < TB TB [Explains the fact that temperature in focal plane of optical telescope cannot exceed TB of a source] beam telescope

HI 21 cm radiative transfer: large scale structure of the IGM LSS: Neutral fraction / Cosmic density / Temperature: Spin, CMB Furlanetto et al. 2006

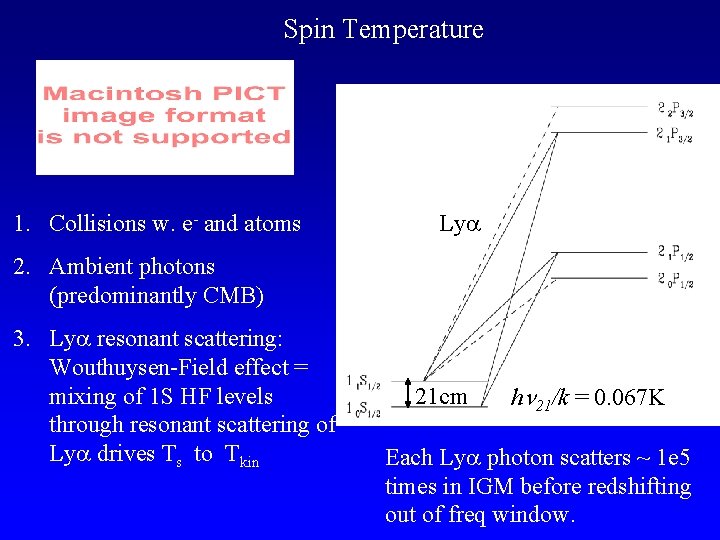
Spin Temperature 1. Collisions w. e- and atoms Ly 2. Ambient photons (predominantly CMB) 3. Ly resonant scattering: Wouthuysen-Field effect = mixing of 1 S HF levels through resonant scattering of Ly drives Ts to Tkin 21 cm h 21/k = 0. 067 K Each Ly photon scatters ~ 1 e 5 times in IGM before redshifting out of freq window.

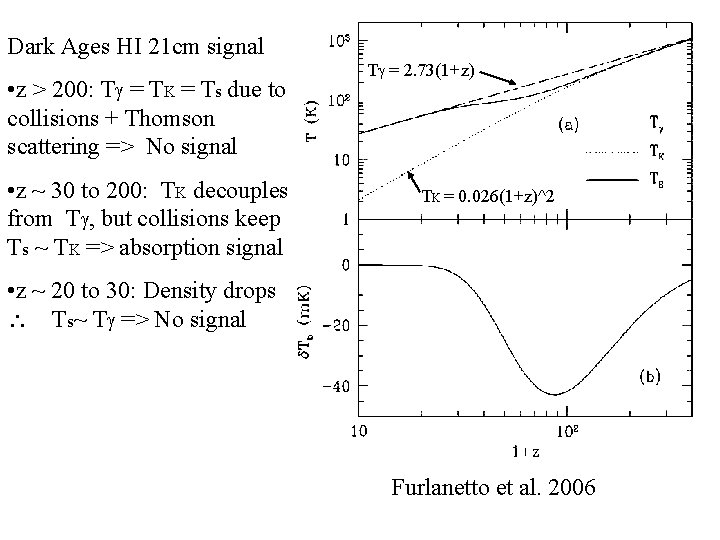
Dark Ages HI 21 cm signal • z > 200: T = TK = Ts due to collisions + Thomson scattering => No signal • z ~ 30 to 200: TK decouples from T , but collisions keep Ts ~ TK => absorption signal T = 2. 73(1+z) TK = 0. 026(1+z)^2 • z ~ 20 to 30: Density drops Ts~ T => No signal Furlanetto et al. 2006

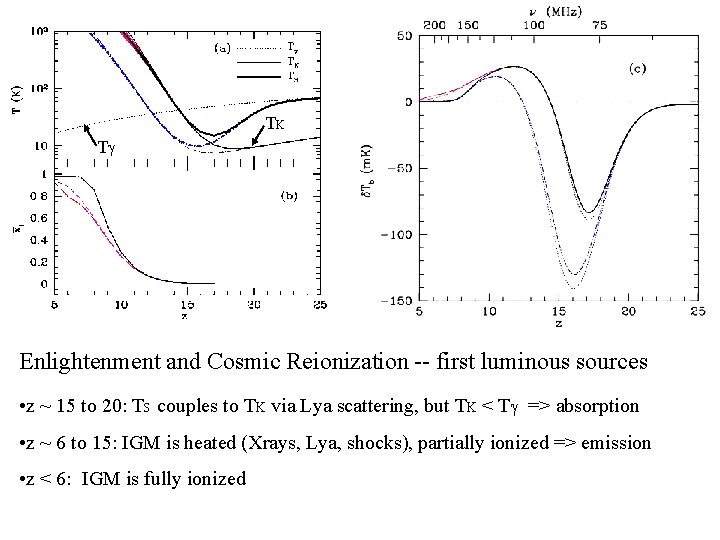
TK T Enlightenment and Cosmic Reionization -- first luminous sources • z ~ 15 to 20: TS couples to TK via Lya scattering, but TK < T => absorption • z ~ 6 to 15: IGM is heated (Xrays, Lya, shocks), partially ionized => emission • z < 6: IGM is fully ionized

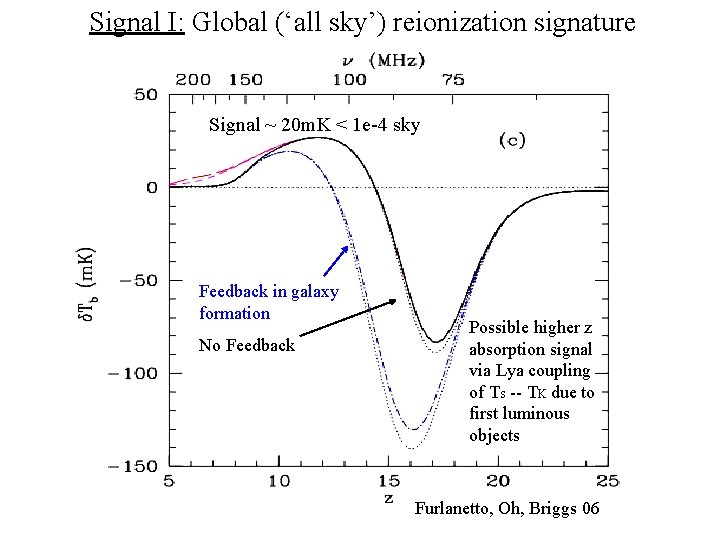
Signal I: Global (‘all sky’) reionization signature Signal ~ 20 m. K < 1 e-4 sky Feedback in galaxy formation No Feedback Possible higher z absorption signal via Lya coupling of Ts -- TK due to first luminous objects Furlanetto, Oh, Briggs 06

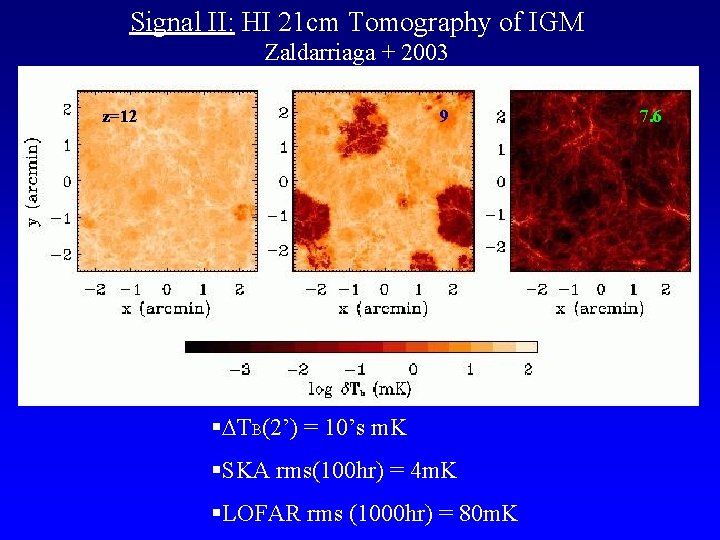
Signal II: HI 21 cm Tomography of IGM Zaldarriaga + 2003 z=12 9 § TB(2’) = 10’s m. K §SKA rms(100 hr) = 4 m. K §LOFAR rms (1000 hr) = 80 m. K 7. 6

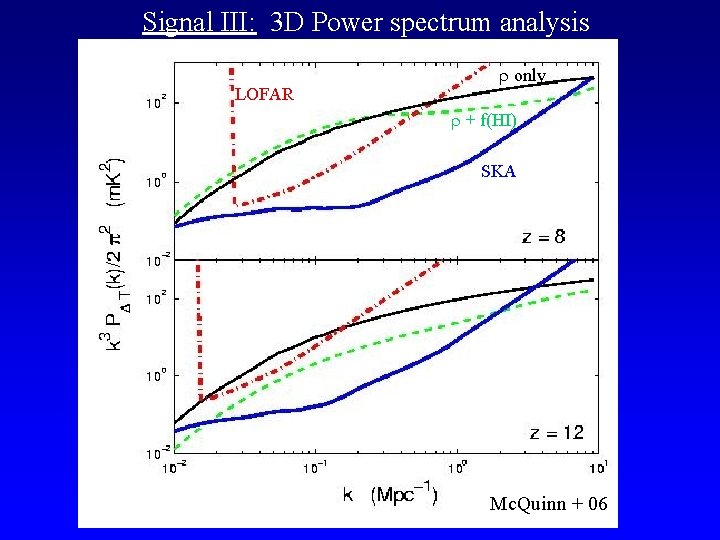
Signal III: 3 D Power spectrum analysis LOFAR only + f(HI) SKA Mc. Quinn + 06

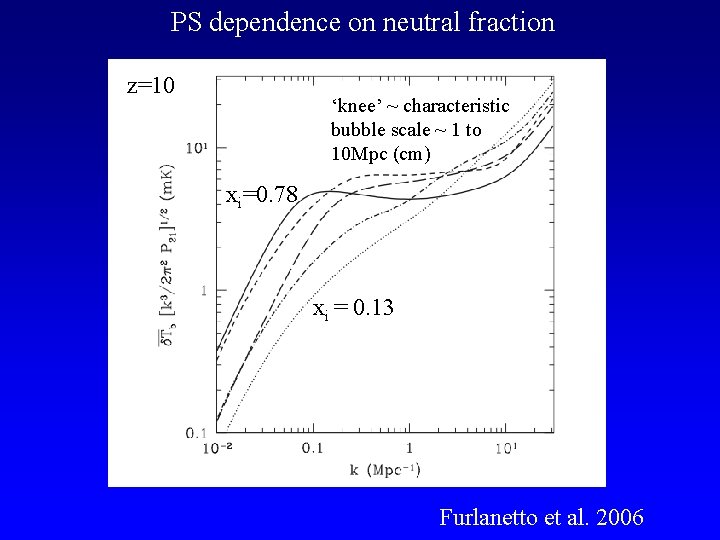
PS dependence on neutral fraction z=10 ‘knee’ ~ characteristic bubble scale ~ 1 to 10 Mpc (cm) xi=0. 78 xi = 0. 13 Furlanetto et al. 2006

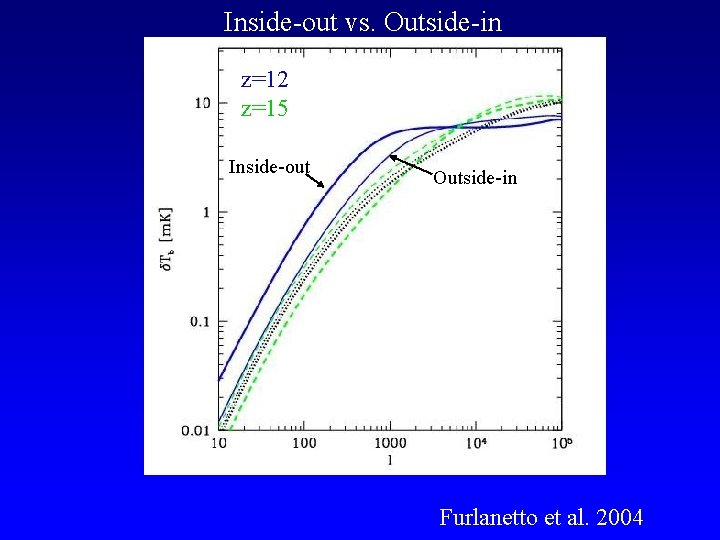
Inside-out vs. Outside-in z=12 z=15 Inside-out Outside-in Furlanetto et al. 2004

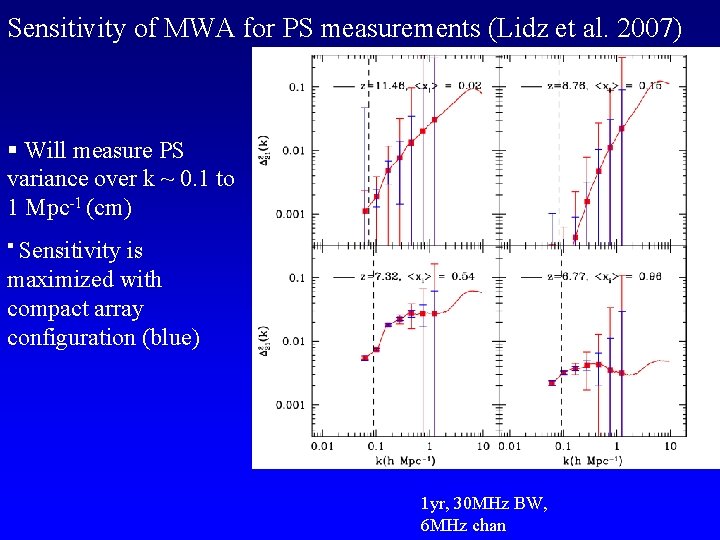
Sensitivity of MWA for PS measurements (Lidz et al. 2007) § Will measure PS variance over k ~ 0. 1 to 1 Mpc-1 (cm) § Sensitivity is maximized with compact array configuration (blue) 1 yr, 30 MHz BW, 6 MHz chan

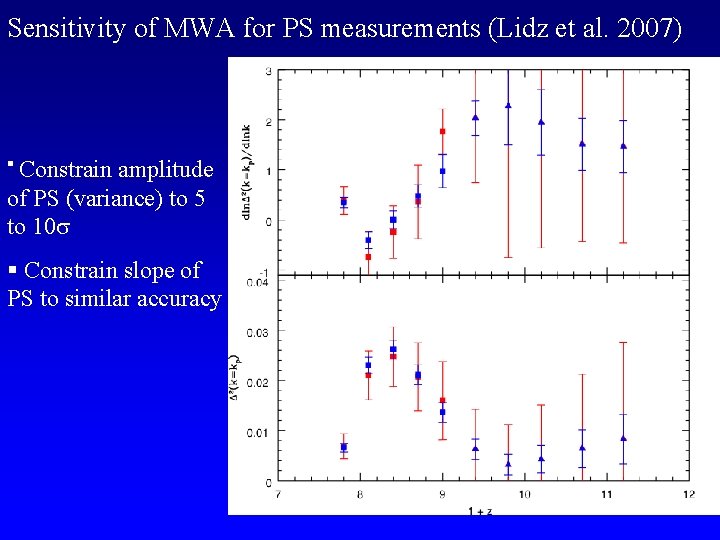
Sensitivity of MWA for PS measurements (Lidz et al. 2007) § Constrain amplitude of PS (variance) to 5 to 10 § Constrain slope of PS to similar accuracy

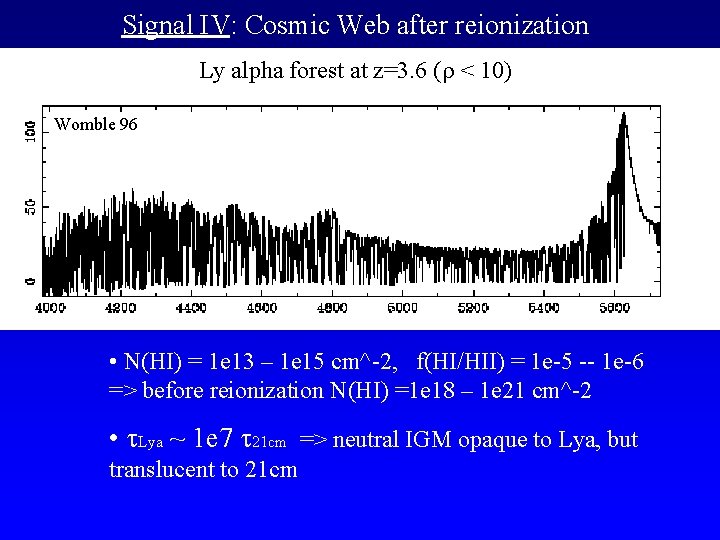
Signal IV: Cosmic Web after reionization Ly alpha forest at z=3. 6 ( < 10) Womble 96 • N(HI) = 1 e 13 – 1 e 15 cm^-2, f(HI/HII) = 1 e-5 -- 1 e-6 => before reionization N(HI) =1 e 18 – 1 e 21 cm^-2 • Lya ~ 1 e 7 21 cm => neutral IGM opaque to Lya, but translucent to 21 cm

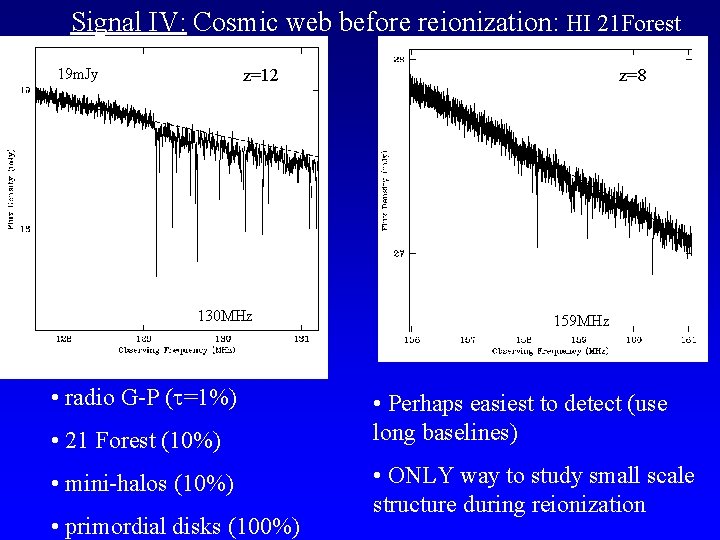
Signal IV: Cosmic web before reionization: HI 21 Forest 19 m. Jy z=12 130 MHz • radio G-P ( =1%) • 21 Forest (10%) • mini-halos (10%) • primordial disks (100%) z=8 159 MHz • Perhaps easiest to detect (use long baselines) • ONLY way to study small scale structure during reionization

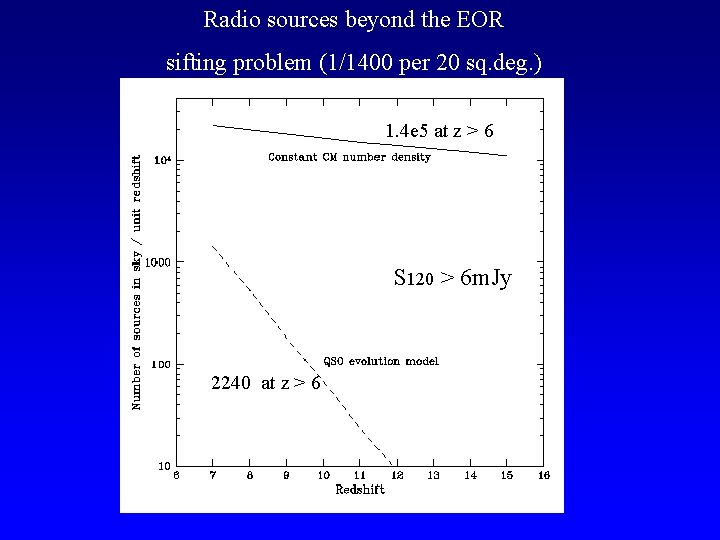
Radio sources beyond the EOR sifting problem (1/1400 per 20 sq. deg. ) 1. 4 e 5 at z > 6 S 120 > 6 m. Jy 2240 at z > 6

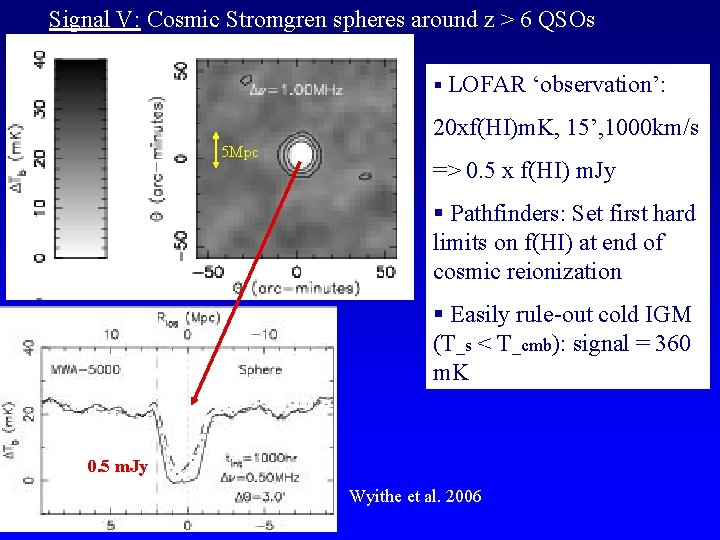
Signal V: Cosmic Stromgren spheres around z > 6 QSOs § LOFAR ‘observation’: 20 xf(HI)m. K, 15’, 1000 km/s 5 Mpc => 0. 5 x f(HI) m. Jy § Pathfinders: Set first hard limits on f(HI) at end of cosmic reionization § Easily rule-out cold IGM (T_s < T_cmb): signal = 360 m. K 0. 5 m. Jy Wyithe et al. 2006

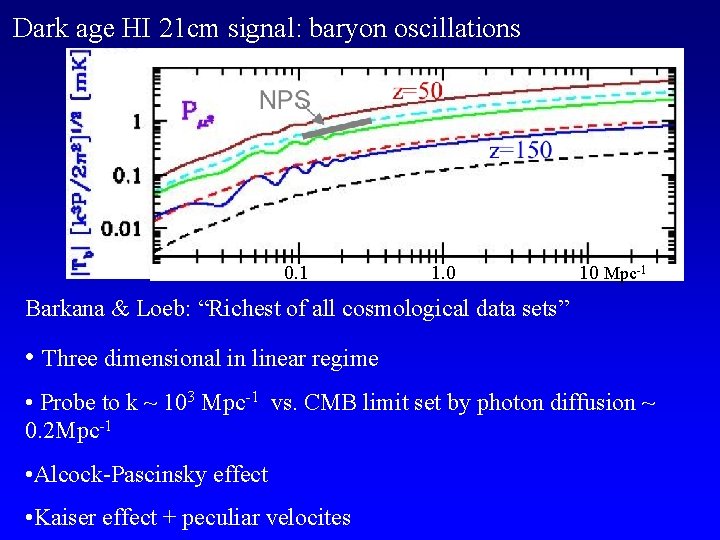
Dark age HI 21 cm signal: baryon oscillations 0. 1 1. 0 10 Mpc-1 Barkana & Loeb: “Richest of all cosmological data sets” • Three dimensional in linear regime • Probe to k ~ 103 Mpc-1 vs. CMB limit set by photon diffusion ~ 0. 2 Mpc-1 • Alcock-Pascinsky effect • Kaiser effect + peculiar velocites

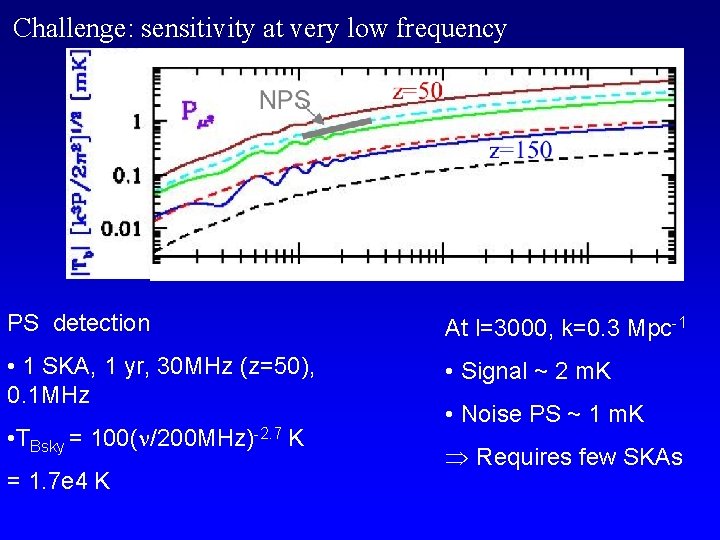
Challenge: sensitivity at very low frequency PS detection At l=3000, k=0. 3 Mpc-1 • 1 SKA, 1 yr, 30 MHz (z=50), 0. 1 MHz • Signal ~ 2 m. K • TBsky = 100( /200 MHz)-2. 7 K = 1. 7 e 4 K • Noise PS ~ 1 m. K Requires few SKAs

BREAK

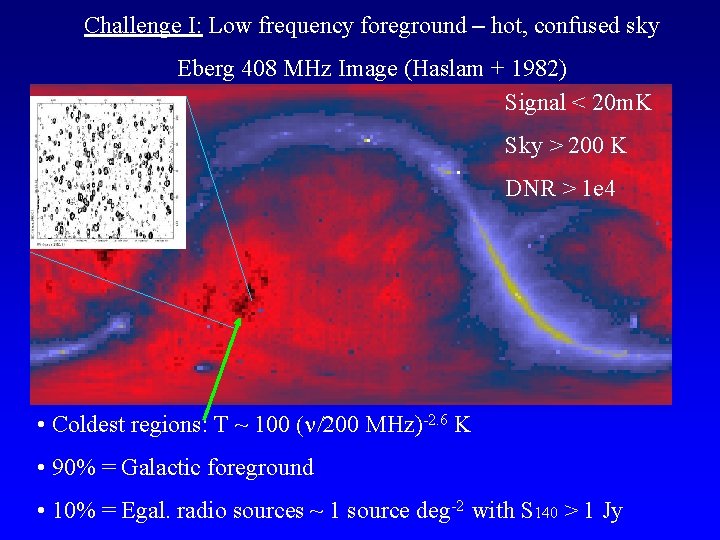
Challenge I: Low frequency foreground – hot, confused sky Eberg 408 MHz Image (Haslam + 1982) Signal < 20 m. K Sky > 200 K DNR > 1 e 4 • Coldest regions: T ~ 100 ( /200 z)-2. 6 K • 90% = Galactic foreground • 10% = Egal. radio sources ~ 1 source deg-2 with S 140 > 1 Jy

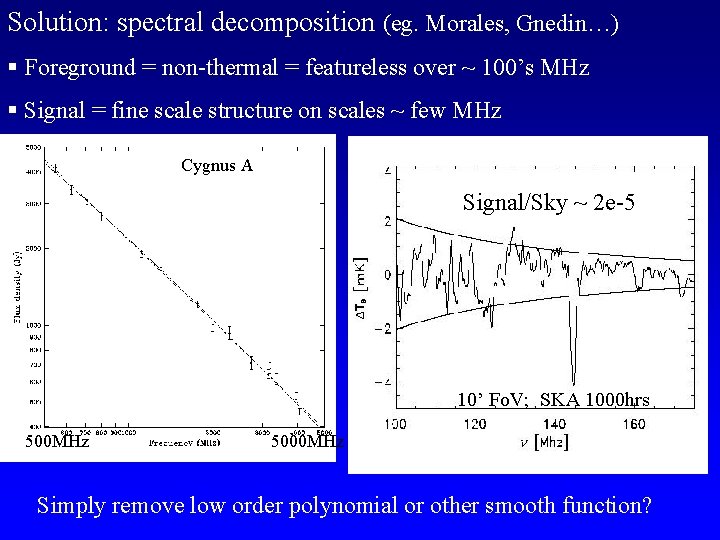
Solution: spectral decomposition (eg. Morales, Gnedin…) § Foreground = non-thermal = featureless over ~ 100’s MHz § Signal = fine scale structure on scales ~ few MHz Cygnus A Signal/Sky ~ 2 e-5 10’ Fo. V; SKA 1000 hrs 500 MHz 5000 MHz Simply remove low order polynomial or other smooth function?

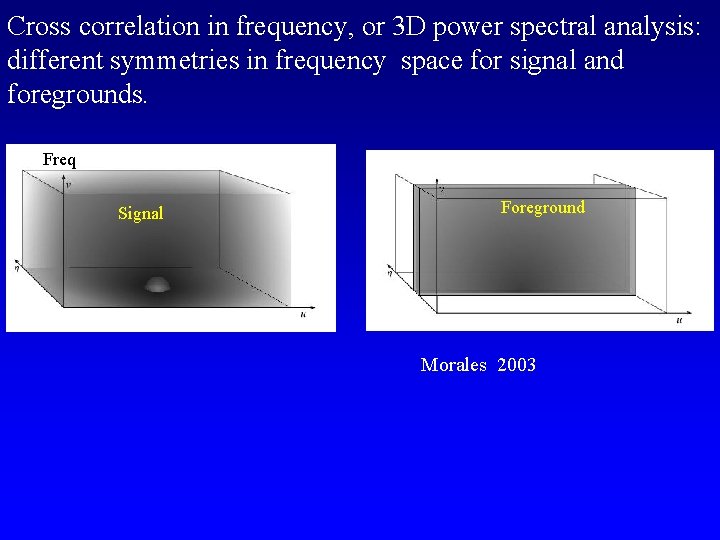
Cross correlation in frequency, or 3 D power spectral analysis: different symmetries in frequency space for signal and foregrounds. Freq Signal Foreground Morales 2003

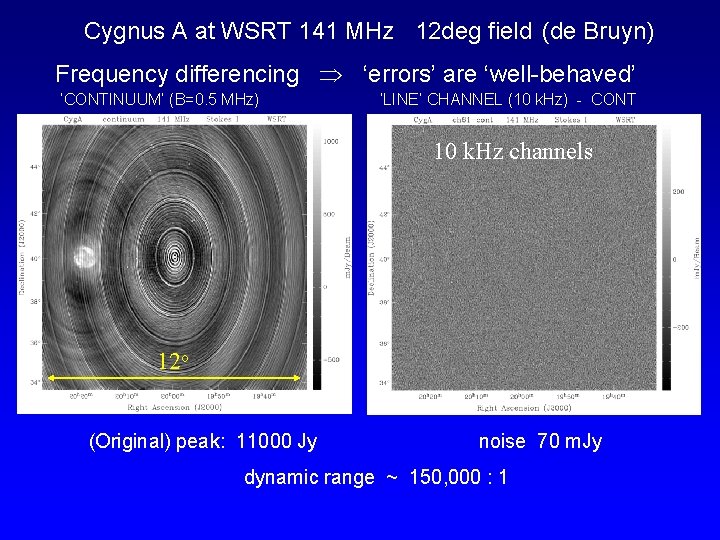
Cygnus A at WSRT 141 MHz 12 deg field (de Bruyn) Frequency differencing ‘errors’ are ‘well-behaved’ ‘CONTINUUM’ (B=0. 5 MHz) ‘LINE’ CHANNEL (10 k. Hz) - CONT 10 k. Hz channels 12 o (Original) peak: 11000 Jy noise 70 m. Jy dynamic range ~ 150, 000 : 1

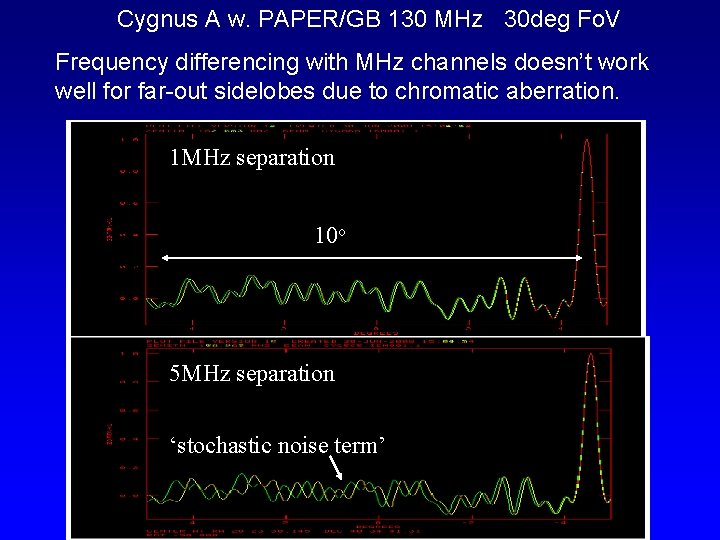
Cygnus A w. PAPER/GB 130 MHz 30 deg Fo. V Frequency differencing with MHz channels doesn’t work well for far-out sidelobes due to chromatic aberration. 1 MHz separation 10 o 5 MHz separation ‘stochastic noise term’

Calibration requirements for point source removal § 20 o x 20 o Fo. V => expect brightest source ~ 34 Jy at 158 MHz § CSS detection: 10 m. K signal over 10’ = 73 u. Jy § required DNR = 34 Jy/73 u. Jy = 4. 6 e 5 § DNR ~ Nant / (21/2 x rms phase error in rad) § 500 element array=> required rms phase error ~ 0. 045 o

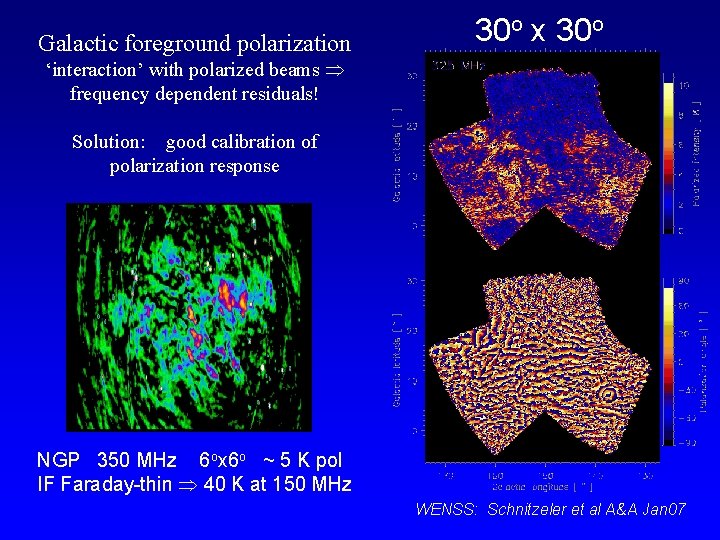
Galactic foreground polarization 30 o x 30 o ‘interaction’ with polarized beams frequency dependent residuals! Solution: good calibration of polarization response NGP 350 MHz 6 ox 6 o ~ 5 K pol IF Faraday-thin 40 K at 150 MHz WENSS: Schnitzeler et al A&A Jan 07

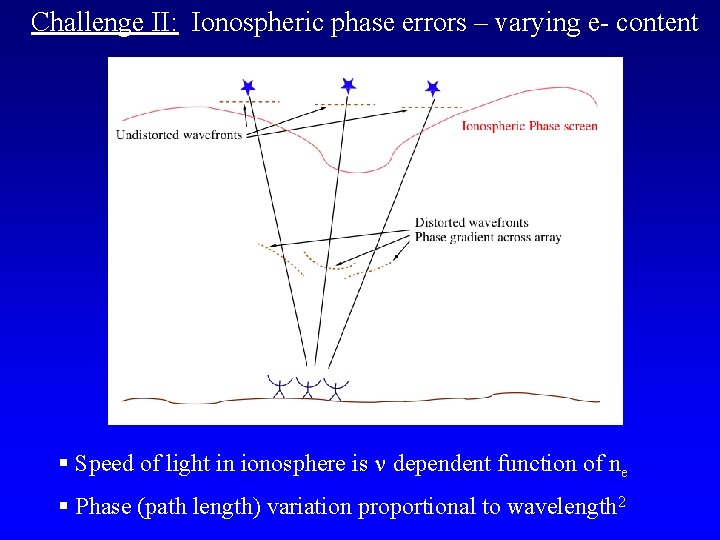
Challenge II: Ionospheric phase errors – varying e- content § Speed of light in ionosphere is dependent function of ne § Phase (path length) variation proportional to wavelength 2

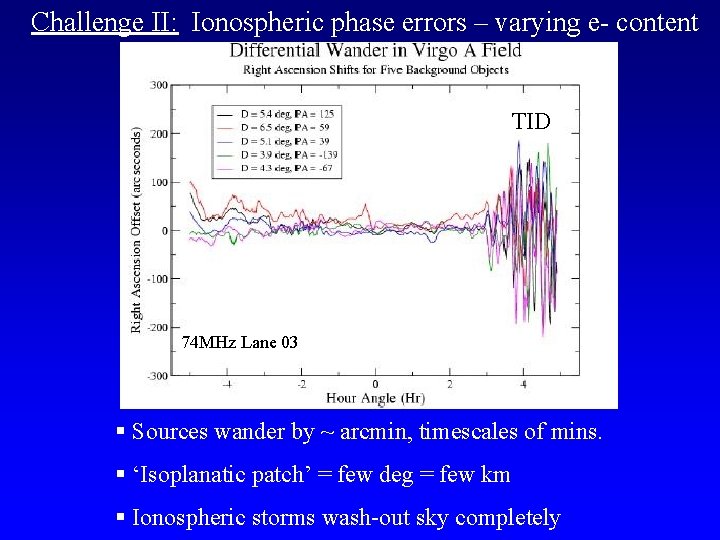
Challenge II: Ionospheric phase errors – varying e- content TID 74 MHz Lane 03 § Sources wander by ~ arcmin, timescales of mins. § ‘Isoplanatic patch’ = few deg = few km § Ionospheric storms wash-out sky completely

Ionospheric phase errors: The Movie Arcmin seeing => problem is not fuzzing-out 21 cm signal itself (typically larger scale) , but calibration errors leading to large (freqdependent) sidelobes from bright sources Solution Direction dependent calibration: Wide field ‘rubber screen’ phase selfcalibration = ‘peeling’ 15’ Virgo A 6 hrs VLA 74 MHz Lane + 02

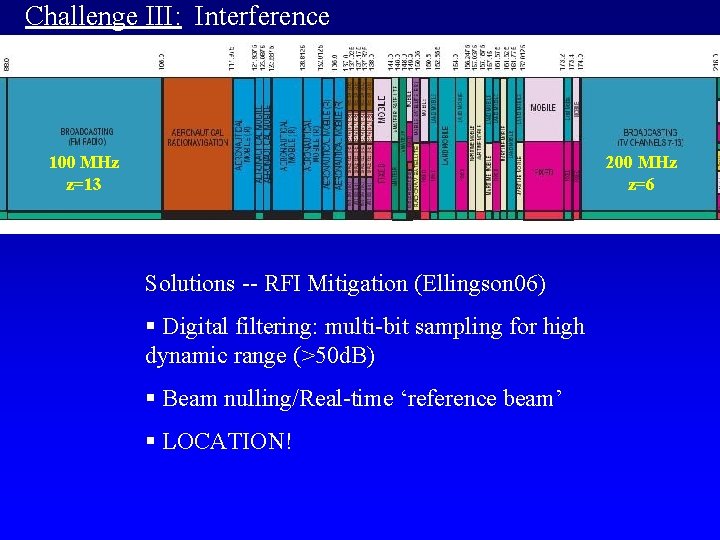
Challenge III: Interference 100 MHz z=13 200 MHz z=6 Solutions -- RFI Mitigation (Ellingson 06) § Digital filtering: multi-bit sampling for high dynamic range (>50 d. B) § Beam nulling/Real-time ‘reference beam’ § LOCATION!

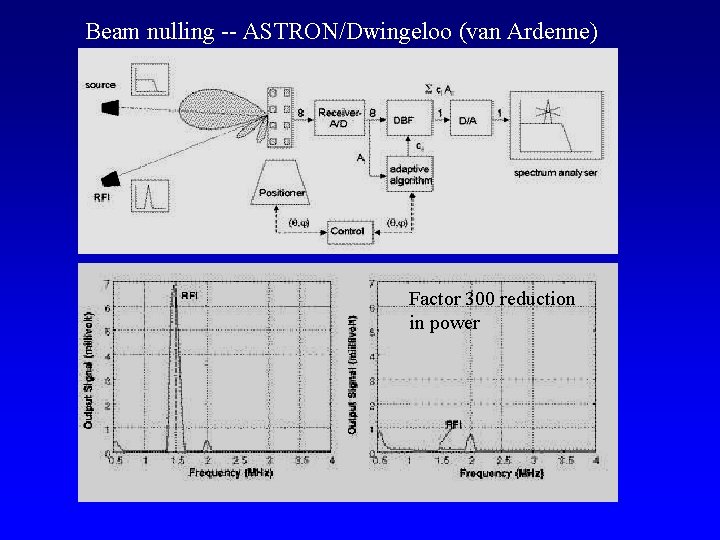
Beam nulling -- ASTRON/Dwingeloo (van Ardenne) Factor 300 reduction in power

VLA-VHF: 180 – 200 MHz Prime focus CSS search Greenhill, Blundell (SAO); Carilli, Perley (NRAO) Leverage: existing telescopes, IF, correlator, operations § $110 K D+D/construction (Cf. A) § First light: Feb 16, 05 § Four element interferometry: May 05 § First limits: Winter 06/07

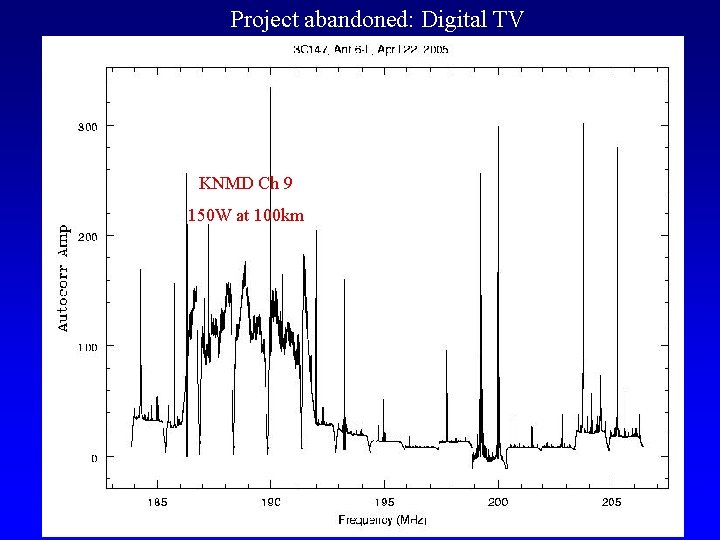
Project abandoned: Digital TV KNMD Ch 9 150 W at 100 km

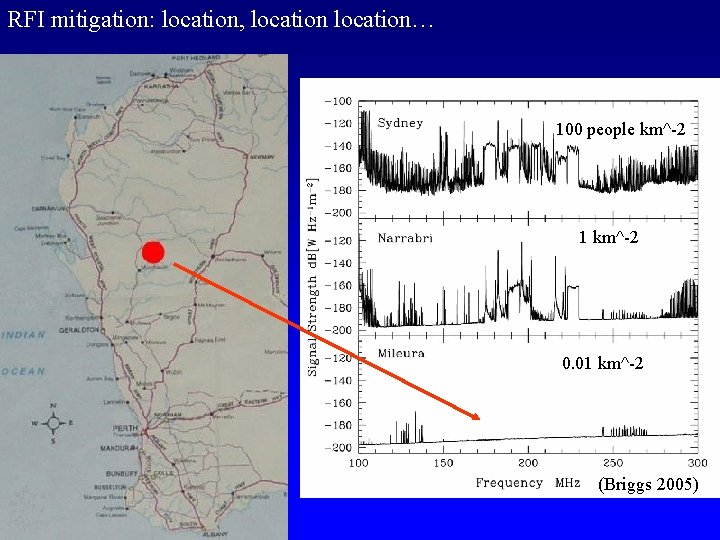
RFI mitigation: location, location… 100 people km^-2 1 km^-2 0. 01 km^-2 (Briggs 2005)

Multiple experiments under-way: ‘pathfinders’ LOFAR (NL) MWA (MIT/Cf. A/ANU) 21 CMA (China) SKA

Complication: ‘Tile’ diffraction beam

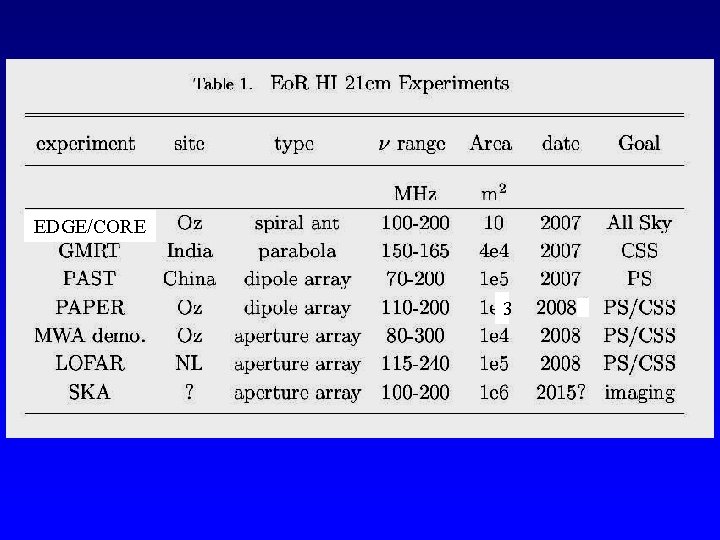
EDGE/CORE 3

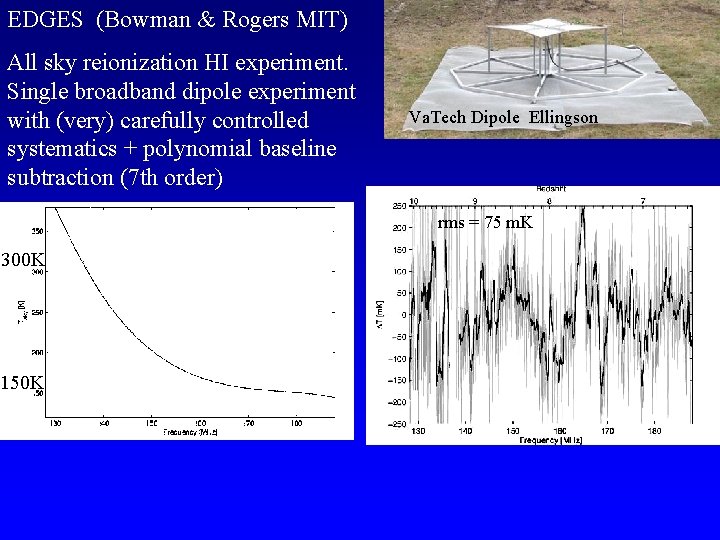
EDGES (Bowman & Rogers MIT) All sky reionization HI experiment. Single broadband dipole experiment with (very) carefully controlled systematics + polynomial baseline subtraction (7 th order) Va. Tech Dipole Ellingson rms = 75 m. K 300 K 150 K

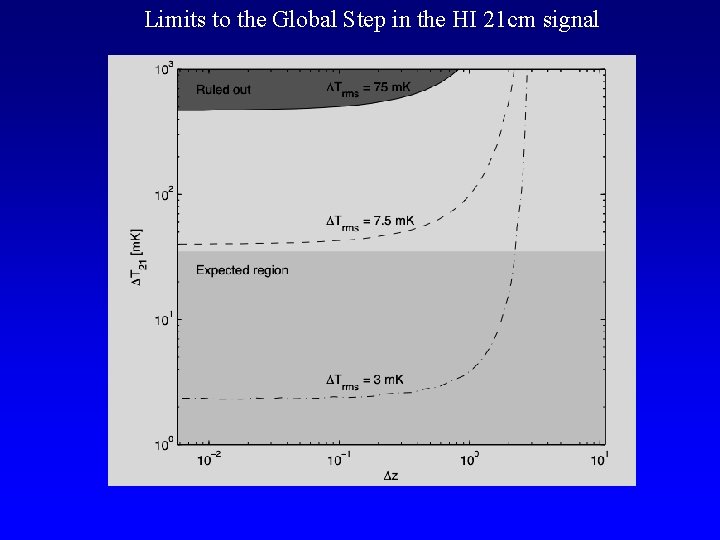
Limits to the Global Step in the HI 21 cm signal

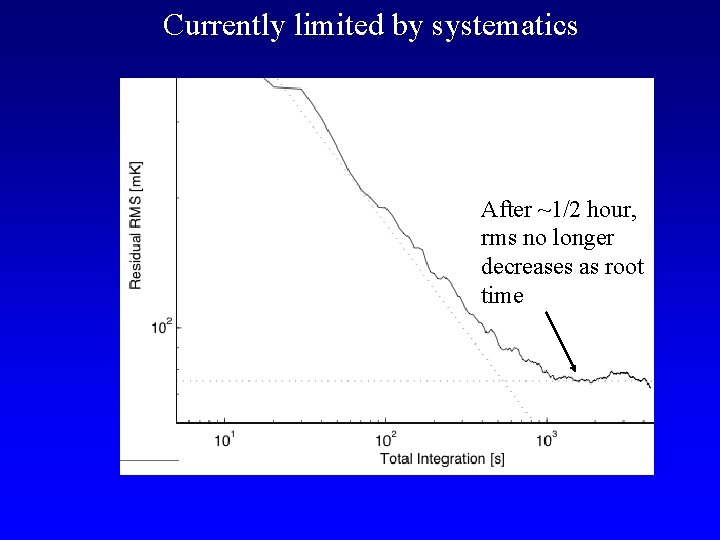
Currently limited by systematics After ~1/2 hour, rms no longer decreases as root time

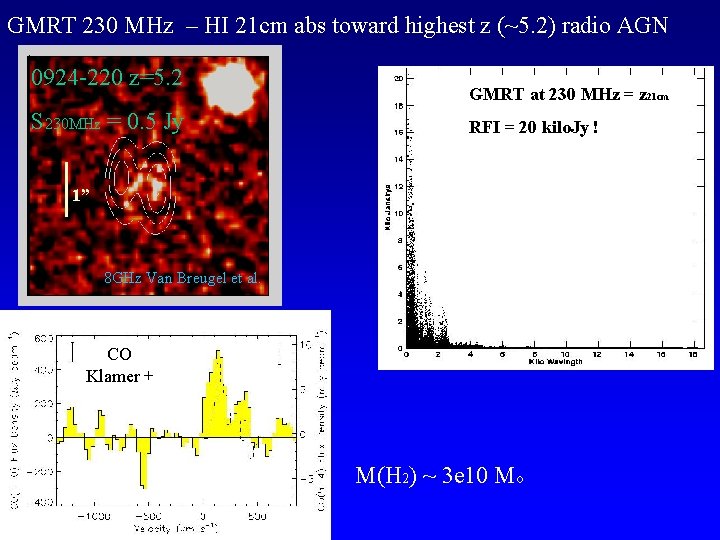
GMRT 230 MHz – HI 21 cm abs toward highest z (~5. 2) radio AGN 0924 -220 z=5. 2 S 230 MHz = 0. 5 Jy GMRT at 230 MHz = z 21 cm RFI = 20 kilo. Jy ! 1” 8 GHz Van Breugel et al. CO Klamer + M(H 2) ~ 3 e 10 Mo

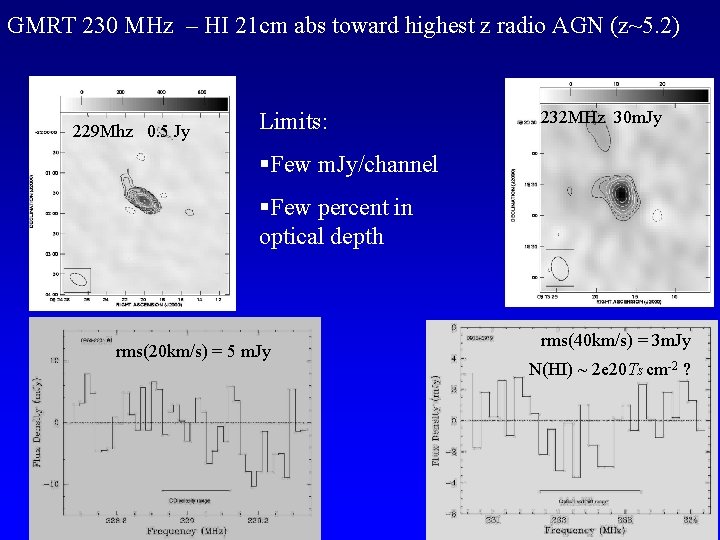
GMRT 230 MHz – HI 21 cm abs toward highest z radio AGN (z~5. 2) 229 Mhz 0. 5 Jy Limits: 232 MHz 30 m. Jy §Few m. Jy/channel §Few percent in optical depth rms(20 km/s) = 5 m. Jy rms(40 km/s) = 3 m. Jy N(HI) ~ 2 e 20 TS cm-2 ?

C. Carilli, A. Datta (NRAO), J. Aguirre (Penn) Focus: Reionization (power spec, CSS, abs)

PAPER: Staged Engineering • Broad band sleeve dipole + flaps • 8 dipole test array in GB (06/07) => 32 station array in WA (2008) to 256 (2009) • FPGA-based ‘pocket correlator’ from Berkeley wireless lab: easily scale-able • S/W Imaging, calibration, PS analysis: AIPY + Miriad/AIPS => Python + CASA, including ionospheric ‘peeling’ calibration BEE 2: 5 FPGAs, 500 Gops/s 100 MHz 200 MHz

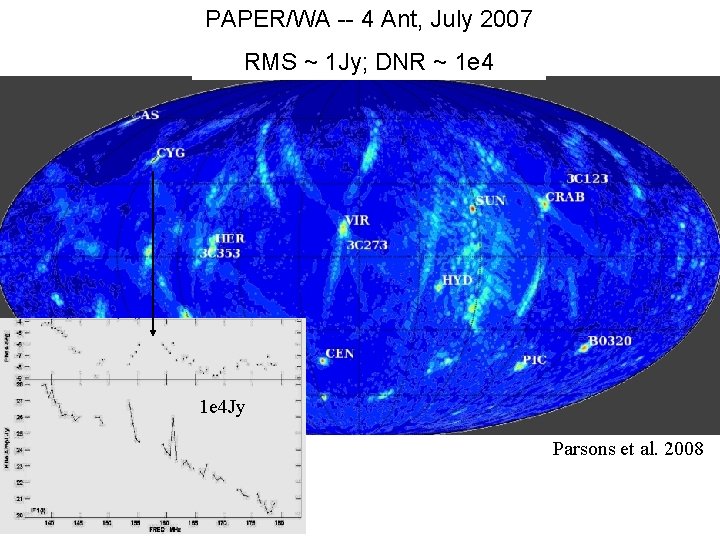
PAPER/WA -- 4 Ant, July 2007 RMS ~ 1 Jy; DNR ~ 1 e 4 Jy Parsons et al. 2008 Cyg. A 1 e 4 Jy

Lunatic fringe: probing the dark ages from the dark side of the Moon C. Carilli (NRAO), Sackler Cosmology Conf, Cambridge, MA, 2008

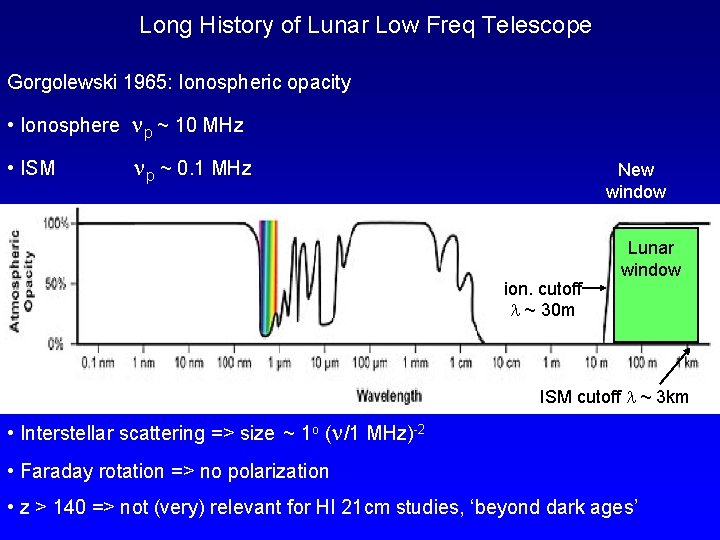
Long History of Lunar Low Freq Telescope Gorgolewski 1965: Ionospheric opacity • Ionosphere p ~ 10 MHz • ISM p ~ 0. 1 MHz New window ion. cutoff ~ 30 m Lunar window ISM cutoff ~ 3 km • Interstellar scattering => size ~ 1 o ( /1 MHz)-2 • Faraday rotation => no polarization • z > 140 => not (very) relevant for HI 21 cm studies, ‘beyond dark ages’

Return to moon is Presidential directive Summary of STSc. I Workshop, Mario Livio, Nov. 2006 “The workshop has identified a few important astrophysical observations that can potentially be carried out from the lunar surface. The two most promising in this respect are: (i) Low-frequency radio observations from the lunar far side to probe structures in the high redshift (10 < z< 100) universe and the epoch of reionization (ii) Lunar ranging experiments…” Our consensus: Lunar imperative awaits lessons from groundarrays

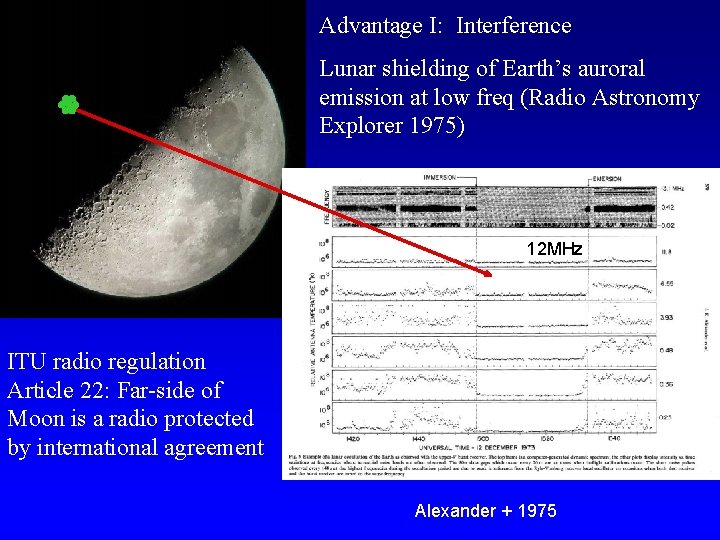
Advantage I: Interference Lunar shielding of Earth’s auroral emission at low freq (Radio Astronomy Explorer 1975) 12 MHz ITU radio regulation Article 22: Far-side of Moon is a radio protected by international agreement Alexander + 1975

Advantage II: Very thin ionosphere -- critical at very low frequencies o Tenuous photoionized layer extending to 100 km o p = 0. 2 to 1 MHz ~ 0. 01 to 0. 1 x Earth o Large day/night variation Clementine (NRL) star tracker

Other practical advantages • Easier deployment: robotic or human • Easier maintenance (no moving parts) • Less demanding hardware tolerances • Very large collecting area, undisturbed for long periods (no weather, no animals, not many people)

Lunar challenges • Array data rates (Tb/s) >> telemetry limits, requiring in situ processing, ie. low power super computing (LOFAR/Blue Gene = 0. 15 MW) • RFI shielding: How far around limb is required? • Thermal cycling (mean): 120 K to 380 K • Radiation environment • Regolith: dielectric/magnetic properties Lunar shielding at 60 k. Hz Takahashi + Woan Apollo 15

Radio astronomy – Probing Cosmic Reionization • ‘Twilight zone’: study of first light limited to near-IR to radio • First constraints: GP, CMBpol => reionization is complex and extended: zreion = 7 to 15 • HI 21 cm: most direct probe of reionization • Low freq pathfinders: All-sky, PS, CSS • SKA: direct imaging of IGM • Lunar array to probe the Dark Ages

END

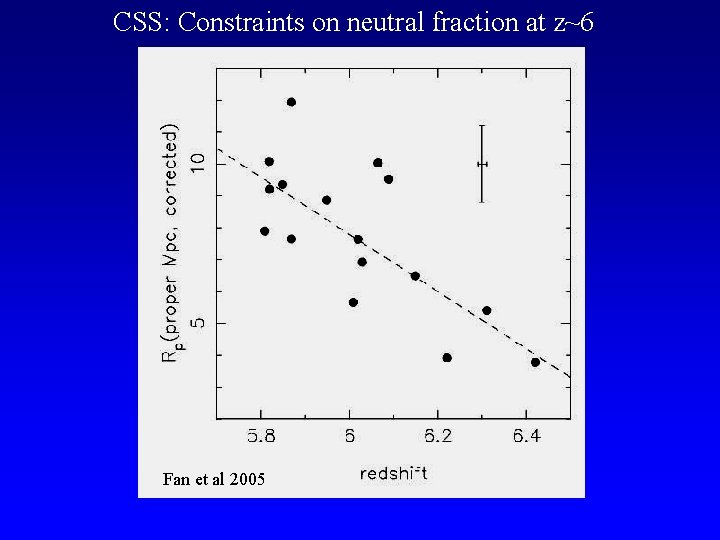
CSS: Constraints on neutral fraction at z~6 Fan et al 2005