PROBABLITY DENSITY FUNCTIONS 0 GAUSSIAN PROBABILITY DENSITY FUNCTION

PROBABLITY DENSITY FUNCTIONS 0

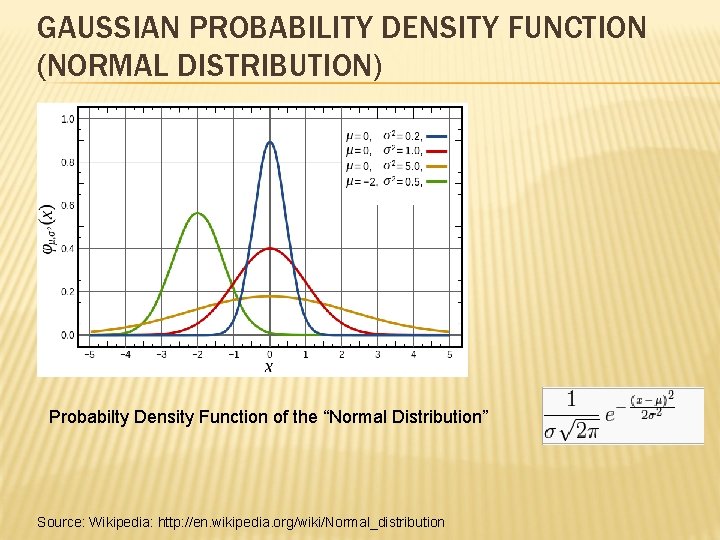
GAUSSIAN PROBABILITY DENSITY FUNCTION (NORMAL DISTRIBUTION) Probabilty Density Function of the “Normal Distribution” Source: Wikipedia: http: //en. wikipedia. org/wiki/Normal_distribution

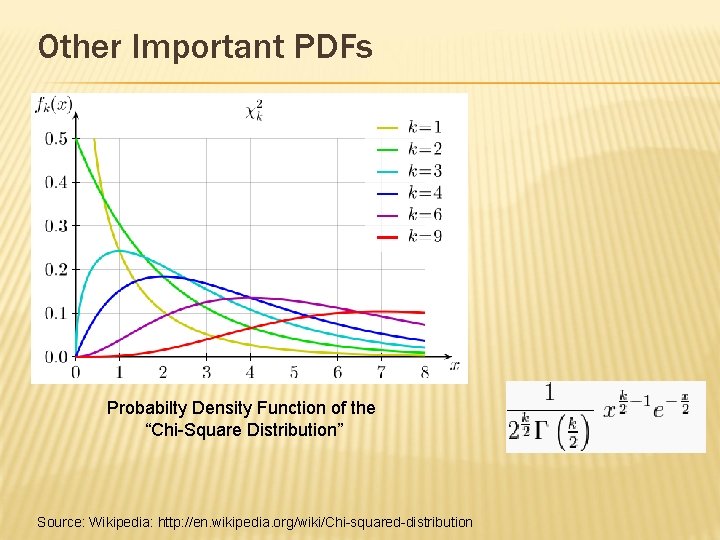
Other Important PDFs Probabilty Density Function of the “Chi-Square Distribution” Source: Wikipedia: http: //en. wikipedia. org/wiki/Chi-squared-distribution

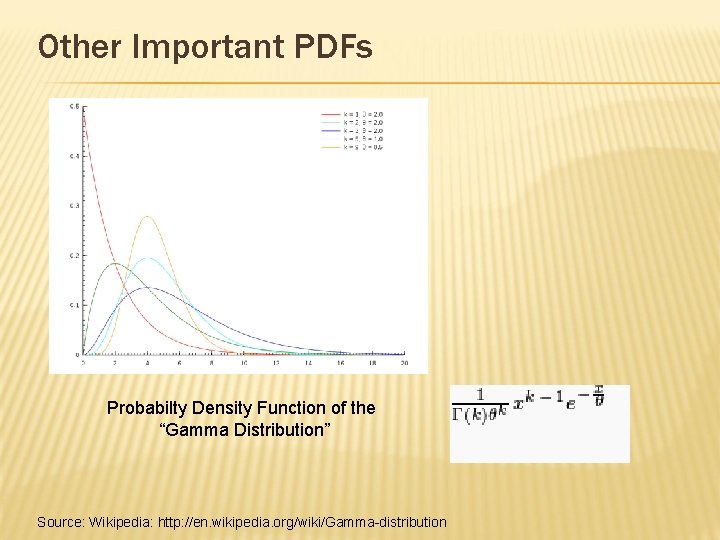
Other Important PDFs Probabilty Density Function of the “Gamma Distribution” Source: Wikipedia: http: //en. wikipedia. org/wiki/Gamma-distribution

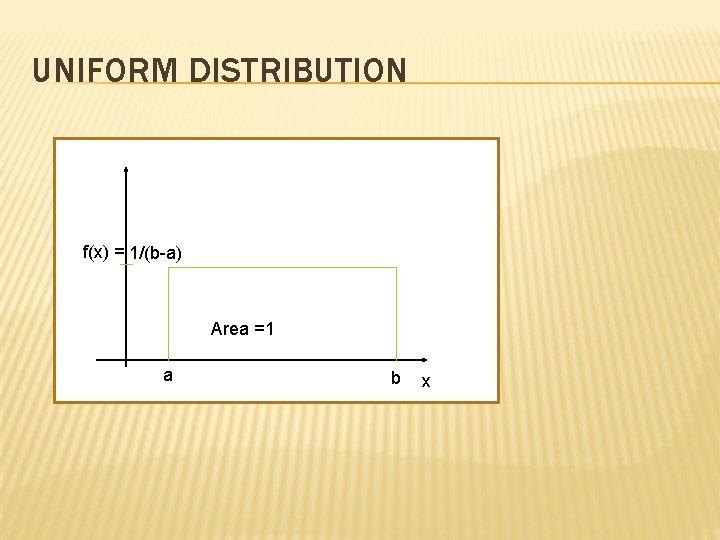
UNIFORM DISTRIBUTION f(x) = 1/(b-a) x Area =1 a b x

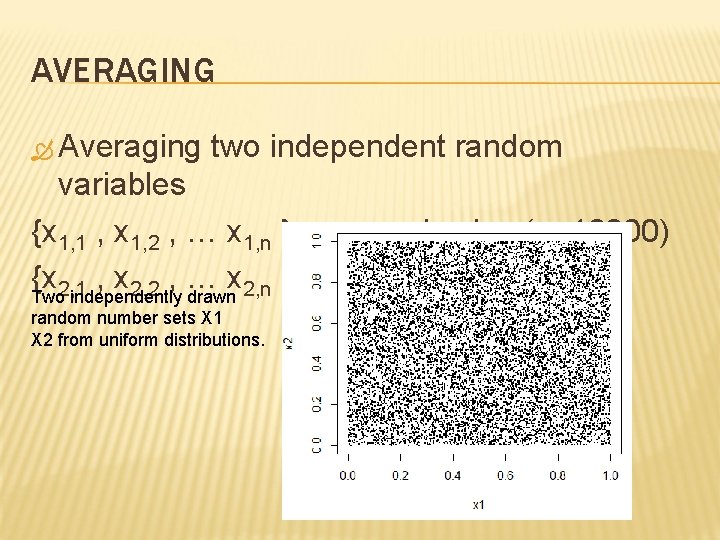
AVERAGING Averaging two independent random variables {x 1, 1 , x 1, 2 , … x 1, n } n: sample size (n=10000) {x , … x } 2, 1 2, 2 2, n Two independently drawn random number sets X 1 X 2 from uniform distributions.

AVERAGING RANDOM VARIABLES Averaging two independent random variables {x 1, 1 , x 1, 2 , … x 1, n } n: sample size (n=10000) {x 2, 1 , x 2, 2 , … x 2, n } Two independently drawn random number sets X 1 X 2 from uniform distributions. Averaged: Y 2, 1=(X 1, 1+X 2, 1)/2

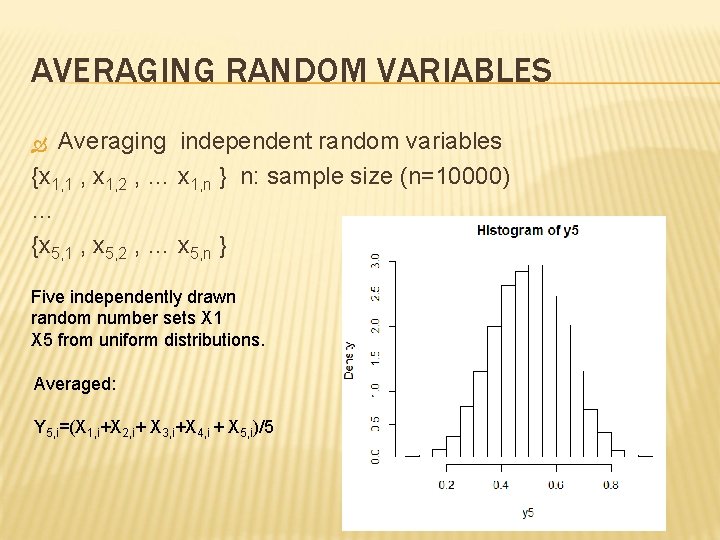
AVERAGING RANDOM VARIABLES Averaging independent random variables {x 1, 1 , x 1, 2 , … x 1, n } n: sample size (n=10000) … {x 5, 1 , x 5, 2 , … x 5, n } Five independently drawn random number sets X 1 X 5 from uniform distributions. Averaged: Y 5, i=(X 1, i+X 2, i+ X 3, i+X 4, i + X 5, i)/5

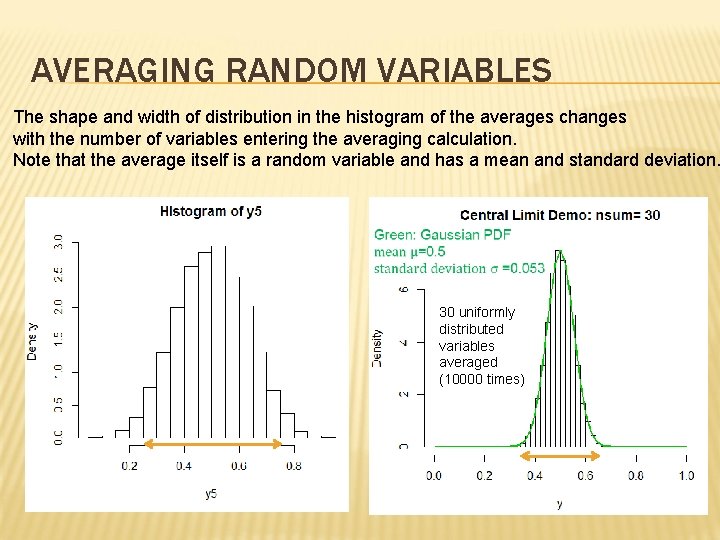
AVERAGING RANDOM VARIABLES The shape and width of distribution in the histogram of the averages changes with the number of variables entering the averaging calculation. Note that the average itself is a random variable and has a mean and standard deviation. 30 uniformly distributed variables averaged (10000 times)

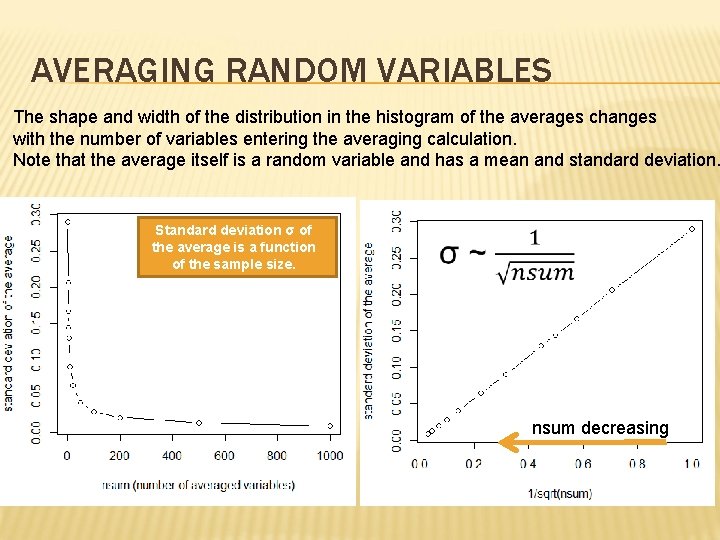
AVERAGING RANDOM VARIABLES The shape and width of the distribution in the histogram of the averages changes with the number of variables entering the averaging calculation. Note that the average itself is a random variable and has a mean and standard deviation. Standard deviation σ of the average is a function of the sample size. nsum decreasing

SUMMARY: During the averaging of randomly sampled data the distribution shape converges towards a Gaussian Distribution with increasing sample size. The larger the sample the smaller the standard deviation σ (i. e. the smaller the uncertainty of the average value). When the samples that enter the averaging are independent, then

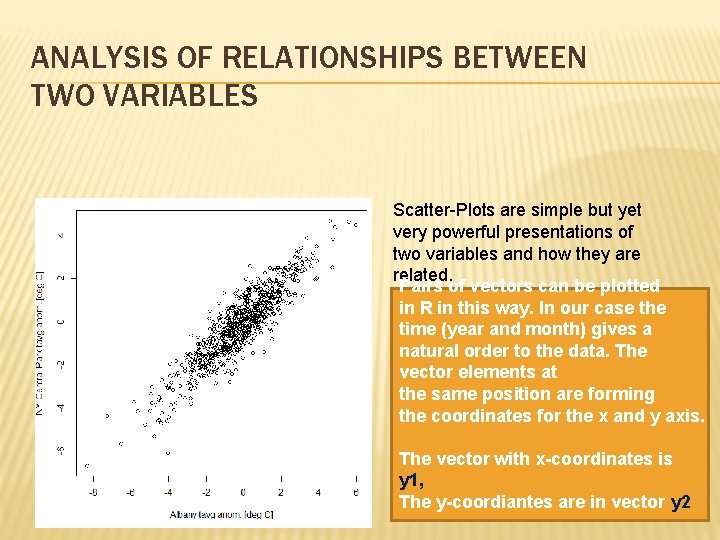
ANALYSIS OF RELATIONSHIPS BETWEEN TWO VARIABLES Scatter-Plots are simple but yet very powerful presentations of two variables and how they are related. Pairs of vectors can be plotted in R in this way. In our case the time (year and month) gives a natural order to the data. The vector elements at the same position are forming the coordinates for the x and y axis. The vector with x-coordinates is y 1, The y-coordiantes are in vector y 2