Probability Venn diagrams Recap Event An event is

Probability & Venn diagrams
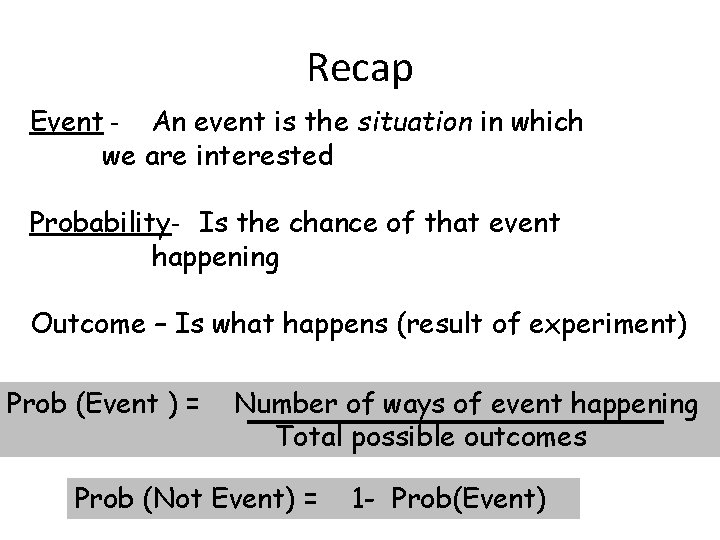
Recap Event - An event is the situation in which we are interested Probability- Is the chance of that event happening Outcome – Is what happens (result of experiment) Prob (Event ) = Number of ways of event happening Total possible outcomes Prob (Not Event) = 1 - Prob(Event)

Mutually Exclusive If A and B are Mutually exclusive then either : A can happen or B can happen, but both can not happen at the same time So P(A) + P(B) =1 If A and B are not Mutually exclusive then they can both happen at the same time So P(A) + P(B) ≠ 1

Venn diagrams These are an excellent way of representing a Probability space We can use them to clearly represent a situation and to calculate corresponding probabilities A dice is rolled an even number is obtained, show this in a Venn diagram A~ event even number A’ 13 5 A 246
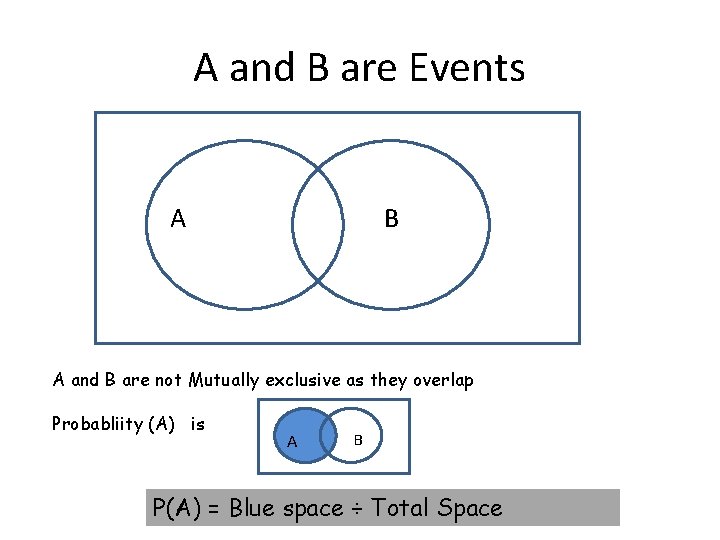
A and B are Events A B A and B are not Mutually exclusive as they overlap Probabliity (A) is A B P(A) = Blue space ÷ Total Space
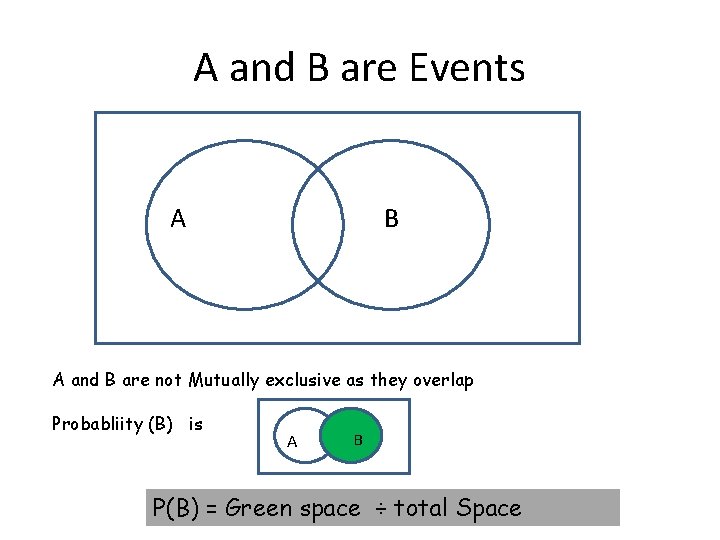
A and B are Events A B A and B are not Mutually exclusive as they overlap Probabliity (B) is A B P(B) = Green space ÷ total Space
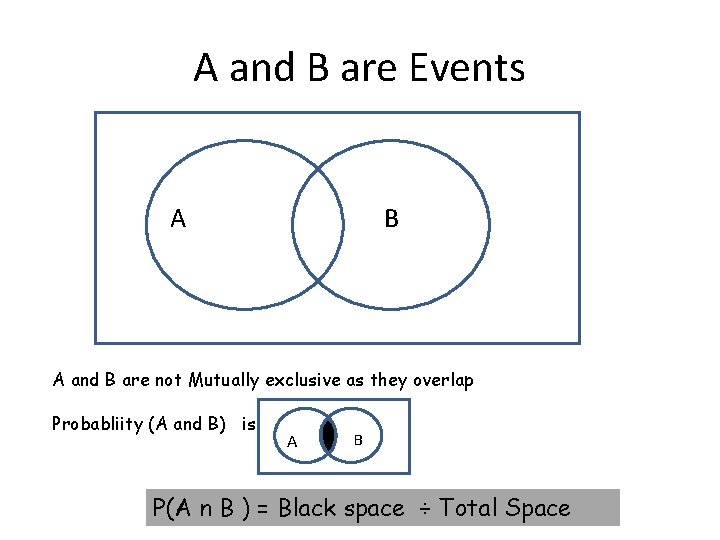
A and B are Events A B A and B are not Mutually exclusive as they overlap Probabliity (A and B) is A B P(A n B ) = Black space ÷ Total Space
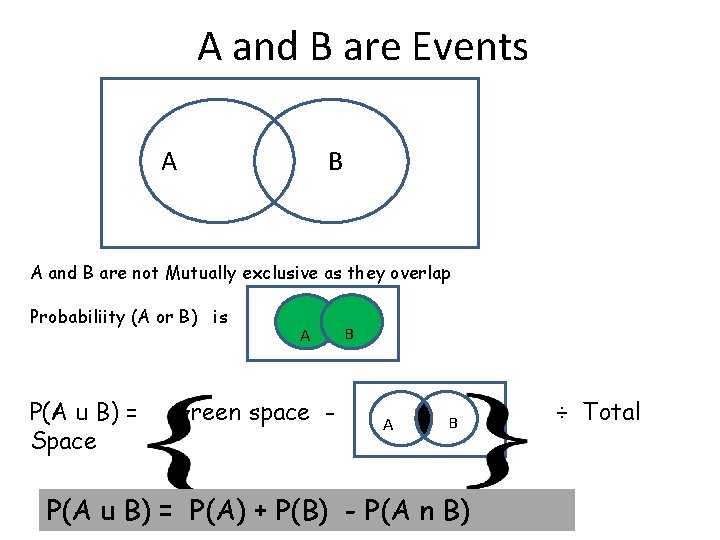
A and B are Events A B A and B are not Mutually exclusive as they overlap Probabiliity (A or B) is P(A u B) = Space A Green space - B A B P(A u B) = P(A) + P(B) - P(A n B) ÷ Total

Example The manager of a factory claims that among his 400 employees: ‾ 312 got a pay rise last year ‾ 248 got increased pension benefits last year ‾ 173 got both pension benefits and pay rise last year ‾ 13 got neither Using last years figures as your guide to this years prospects, calculate the probability of: a) b) c) d) e) Getting a pay rise Not getting a pay rise Getting both a pay rise and pension benefits Getting no pay rise or benefit increase Getting a pay rise or benefits Step 1 – Fill in the Venn diagram
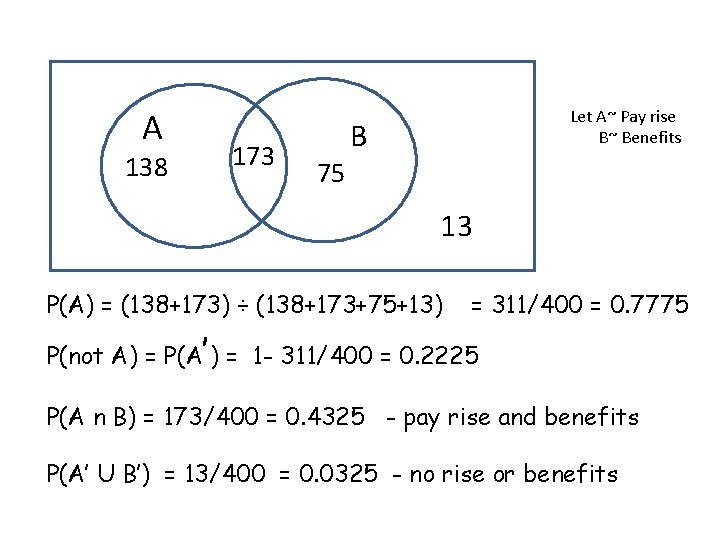
A 138 173 Let A~ Pay rise B~ Benefits B 75 13 P(A) = (138+173) ÷ (138+173+75+13) = 311/400 = 0. 7775 P(not A) = P(A’) = 1 - 311/400 = 0. 2225 P(A n B) = 173/400 = 0. 4325 - pay rise and benefits P(A’ U B’) = 13/400 = 0. 0325 - no rise or benefits

Conditional Probability These are the probabilities calculated on the basis that something has already happened For example : —The probability that I will pay my electricity bill given that have just been paid —The probability that my students will turn upto class given that it is a sunny day The emphasis is that the probability is influenced by something that has already happened. If these two events are A and B then they are not INDEPENDENT we write P(A|B) ~ P(A given B)

P(A|B) ~ P(A given B has occurred) If B has already happened then our event must be somewhere in B B A BUT, How can A happen if our event must be in the B space ? We can only be in the following Space on our Venn Diagram B A And so Our Probability P(A|B) is the ratio of Green Space ÷ Red space A B

Example 1 P(A)=0. 3 ; P(B)= 0. 4 and P(A|B)=0. 5 Find 1 - P(A n B) 2 - P(A u B) 3 - P(A|B’ ) Fill in the Venn diagram 1 - P(A|B) is 0. 5 so =0. 5 + A 0. 1 0. 2 B 0. 2 0. 5 P(A|B) = P(A n B)/P(B) so P(A n B) = 0. 5 x 0. 4 = 0. 2 2 - P( A u B) = P(A) + P(B) – P(A n B) = 0. 3 + 0. 4 – 0. 2 = 0. 5 3 - P(A/B’) ~ P( A given Not B) = P(A n B’)/P(B’) = (0. 3 -0. 2)/(1 -0. 4) = 0. 1/0. 6 = 0. 1667 A P(A n B’) B

Example 2 One hundred cars are entered for an MOT test. The test comprises two parts : Mechanical and electrical The car must pass both parts to be given an MOT certificate. Half the cars pass the Electrical 62 pass the Mechanical test 15 pass the Electrical but fail the electrical Find the probability that a car chosen at random a) Passes overall (i. e passes both tests) b) Fails on one test only c) Given that it had failed, failed the Mechanical only Draw a Venn diagram

We want to find Let M-mechanical E-electrical In language of Probability we need to find a) P(M and E) ~ P(M n E) - passes both mechanical and electrical b) P(M or E) ~ P( M u B) - passes mechanical or electrical or both So we want P(M’ or E’) ~ P( M’ u B’) - fails mechanical or electrical or both c) Let F~ Fail [= 1 - P(M n E)] so we want P(M’ | F) = P(E|F) = P(E n F) / P(F)

Given P(E) = 50/100 P(M) = 62/100 P(E n M’) = 15/100 = 0. 5 = 0. 62 = 0. 15 E 0. 15 0. 35 M 0. 27 a) 100 cars and 35 pass overall so P(E n M) = 0. 35 b) P(E u M) = P(E) + P(M) – P(E n M) = 0. 5 +0. 65 – 0. 35 = 0. 75 c) Given the car fails what chance that it failed Mechanical only P(En F)=0. 15 P(F) = 1 -P(Pass) = 1 -0. 35 = 0. 65 P(M’|F) = P(E n F)/P(F) = 0. 15/0. 65 = 15/65 = 0. 2307
- Slides: 16