Probability Trees A Graphical Method for Complicated Probability

Probability Trees A Graphical Method for Complicated Probability Problems

Example: Southwest Energy q A Southwest Energy Company pipeline has 3 safety shutoff valves in case the line starts to leak. q The valves are designed to operate independently of one another: • 7% chance that valve 1 will fail • 10% chance that valve 2 will fail • 5% chance that valve 3 will fail q If there is a leak in the line, find the following probabilities: a. b. c. d. That all three valves operate correctly all three valves fail only one valve operates correctly at least one valve operates correctly

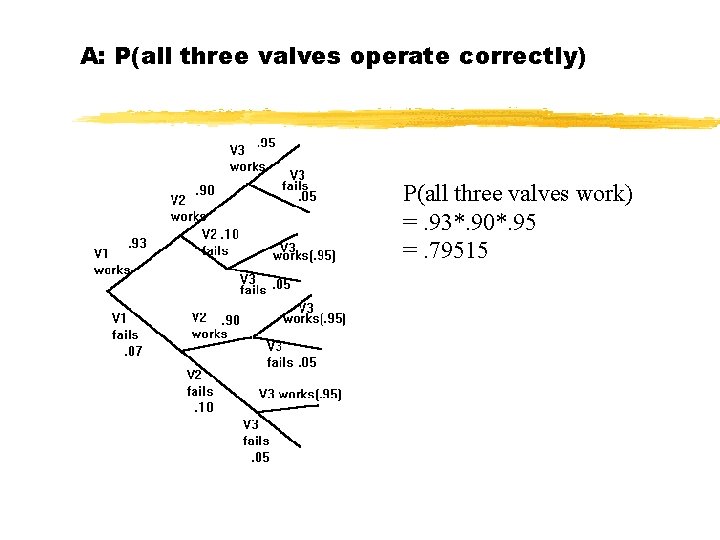
A: P(all three valves operate correctly) P(all three valves work) =. 93*. 90*. 95 =. 79515

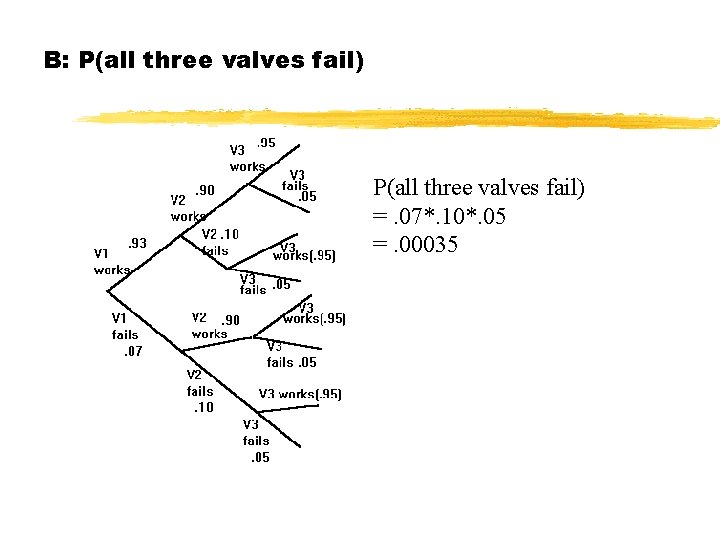
B: P(all three valves fail) =. 07*. 10*. 05 =. 00035

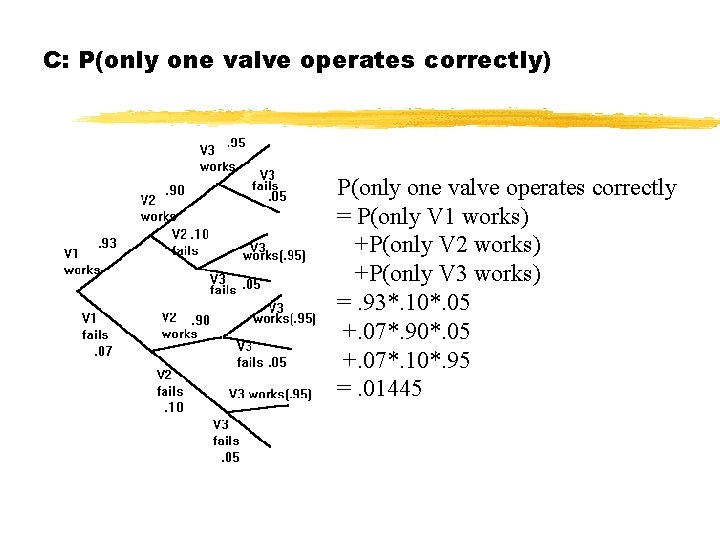
C: P(only one valve operates correctly) P(only one valve operates correctly = P(only V 1 works) +P(only V 2 works) +P(only V 3 works) =. 93*. 10*. 05 +. 07*. 90*. 05 +. 07*. 10*. 95 =. 01445

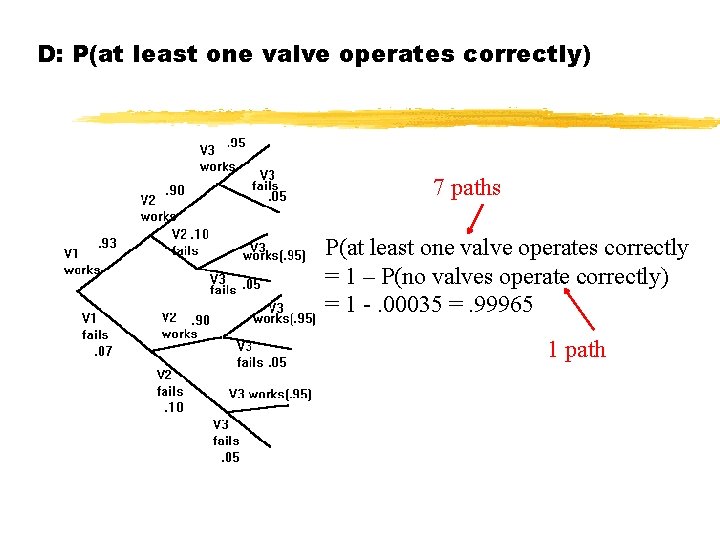
D: P(at least one valve operates correctly) 7 paths P(at least one valve operates correctly = 1 – P(no valves operate correctly) = 1 -. 00035 =. 99965 1 path

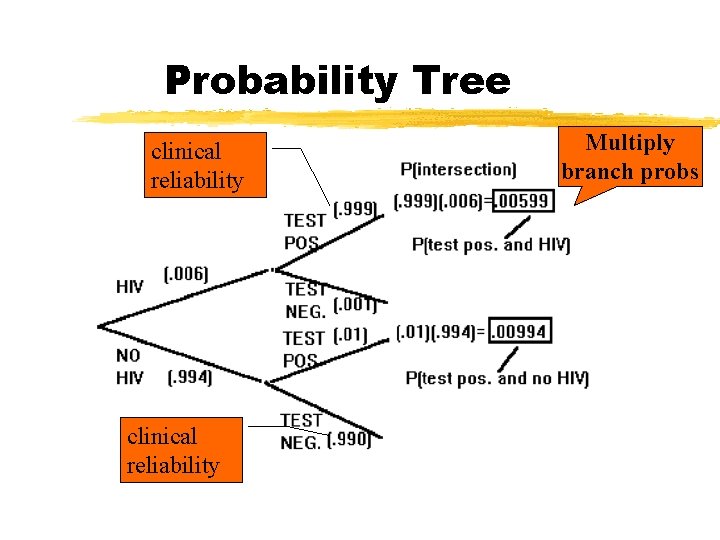
Example: AIDS Testing z V={person has HIV}; CDC: Pr(V)=. 006 z P : test outcome is positive (test indicates HIV present) z N : test outcome is negative z clinical reliabilities for a new HIV test: 1. If a person has the virus, the test result will be positive with probability. 999 2. If a person does not have the virus, the test result will be negative with probability. 990

Question 1 z. What is the probability that a randomly selected person will test positive?

Probability Tree Approach z. A probability tree is a useful way to visualize this problem and to find the desired probability.

Probability Tree clinical reliability Multiply branch probs

Question 1 Answer z. What is the probability that a randomly selected person will test positive? z. Pr(P )=. 00599 +. 00994 =. 01593

Question 2 z If your test comes back positive, what is the probability that you have HIV? (Remember: we know that if a person has the virus, the test result will be positive with probability. 999; if a person does not have the virus, the test result will be negative with probability. 990). z Looks very reliable

Question 2 Answer two sequences of branches lead to positive test; only 1 sequence represented people who have HIV. Pr(person has HIV given that test is positive) =. 00599/(. 00599+. 00994) =. 376

Summary z. Question 1: z. Pr(P ) =. 00599 +. 00994 =. 01593 z. Question 2: two sequences of branches lead to positive test; only 1 sequence represented people who have HIV. Pr(person has HIV given that test is positive) =. 00599/(. 00599+. 00994) =. 376

Recap z We have a test with very high clinical reliabilities: 1. If a person has the virus, the test result will be positive with probability. 999 2. If a person does not have the virus, the test result will be negative with probability. 990 z But we have extremely poor performance when the test is positive: Pr(person has HIV given that test is positive) =. 376 z In other words, 62. 4% of the positives are false positives! Why? z When the characteristic the test is looking for is rare, most positives will be false.