PROBABILITY TREE DIAGRAMS Independent events Probability with replacement

PROBABILITY & TREE DIAGRAMS Independent events Probability with replacement

WHAT ARE TREE DIAGRAMS A way of showing the possibilities of two or more events Simple diagram we use to calculate the probabilities of two or more events

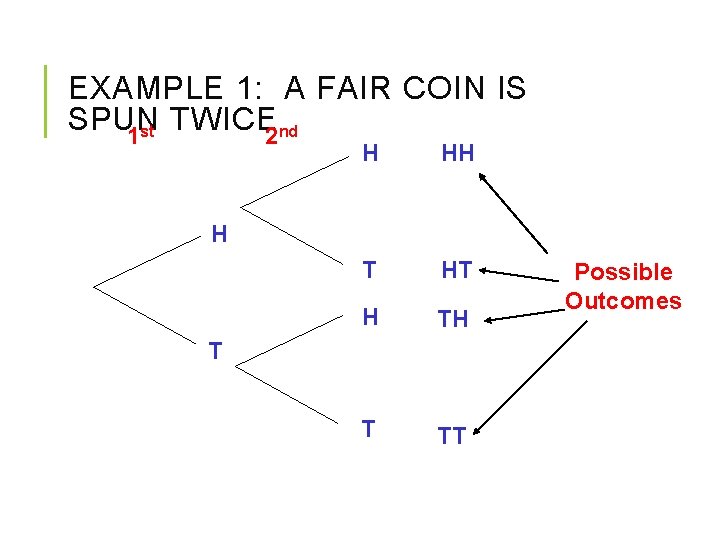
EXAMPLE 1: A FAIR COIN IS SPUN TWICE 2 nd 1 st H HH T HT H TH T TT H T Possible Outcomes

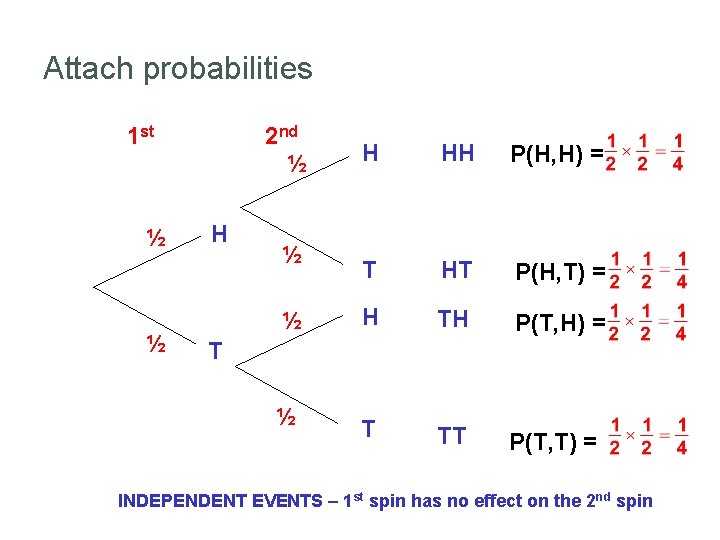
Attach probabilities 1 st ½ ½ 2 nd ½ H H HH P(H, H) = T HT P(H, T) = ½ H TH P(T, H) = ½ T TT P(T, T) = ½ T INDEPENDENT EVENTS – 1 st spin has no effect on the 2 nd spin

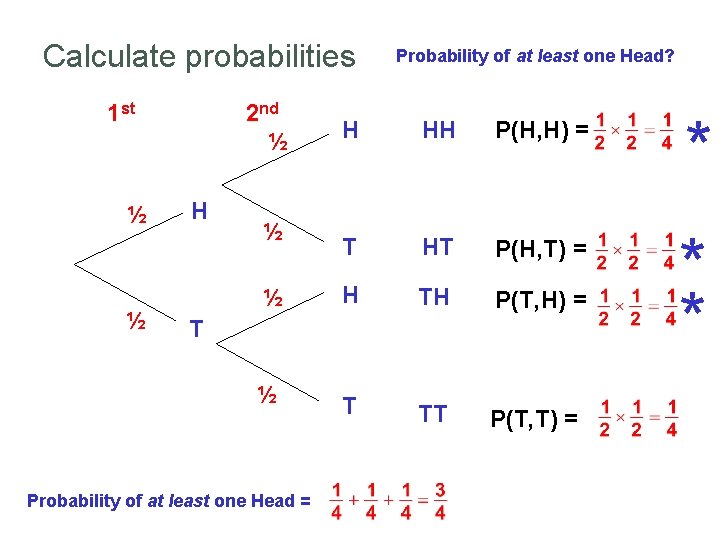
Calculate probabilities 1 st ½ ½ 2 nd ½ H Probability of at least one Head? H HH P(H, H) = * T HT P(H, T) = ½ H TH P(T, H) = * * ½ T TT P(T, T) = ½ T Probability of at least one Head =

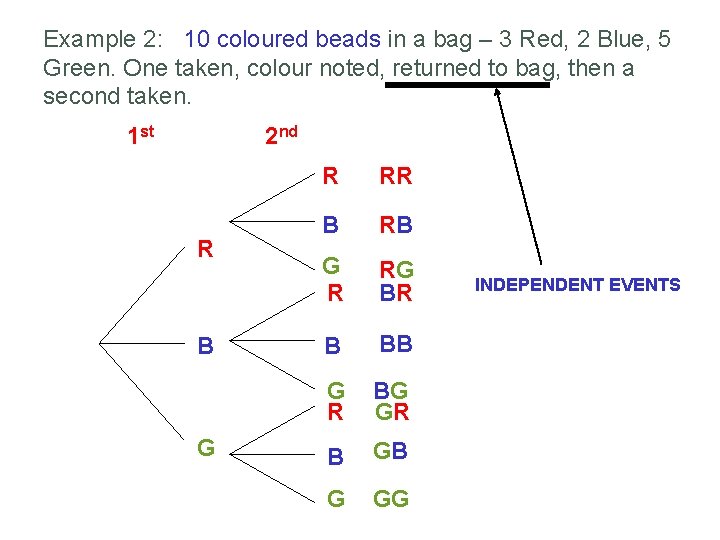
Example 2: 10 coloured beads in a bag – 3 Red, 2 Blue, 5 Green. One taken, colour noted, returned to bag, then a second taken. 1 st 2 nd R B G R RR B RB G R RG BR B BB G R BG GR B GB G GG INDEPENDENT EVENTS

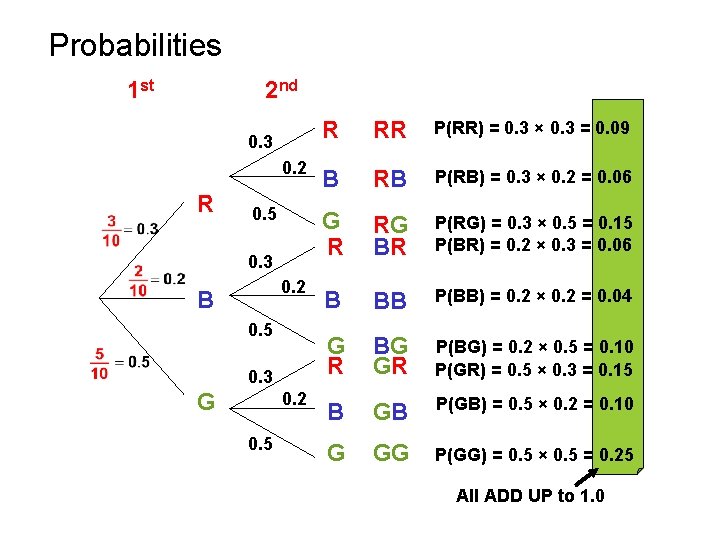
Probabilities 1 st 2 nd 0. 3 0. 2 R 0. 5 0. 3 0. 2 B 0. 5 0. 3 G 0. 2 0. 5 R RR P(RR) = 0. 3 × 0. 3 = 0. 09 B RB P(RB) = 0. 3 × 0. 2 = 0. 06 G R RG BR P(RG) = 0. 3 × 0. 5 = 0. 15 P(BR) = 0. 2 × 0. 3 = 0. 06 B BB P(BB) = 0. 2 × 0. 2 = 0. 04 G R BG GR P(BG) = 0. 2 × 0. 5 = 0. 10 P(GR) = 0. 5 × 0. 3 = 0. 15 B GB P(GB) = 0. 5 × 0. 2 = 0. 10 G GG P(GG) = 0. 5 × 0. 5 = 0. 25 All ADD UP to 1. 0