Probability Theory Bayes theorem Perfect secrecy definition some

- Probability Theory: Bayes’ theorem - Perfect secrecy: definition, some proofs, examples: one-time pad; simple secret sharing - Entropy: Definition, Huffman coding property, unicity distance Information-Theoretic Secrecy CSCI 381 Fall 2005 GWU Reference: Stinson CS 284/Spring 04/GWU/Vora/Shannon Secrecy
![Bayes’ Theorem If Pr[y] > 0 then Pr[x|y] = Pr[x]Pr[y|x]/ x X Pr[x]Pr[y|x] What Bayes’ Theorem If Pr[y] > 0 then Pr[x|y] = Pr[x]Pr[y|x]/ x X Pr[x]Pr[y|x] What](http://slidetodoc.com/presentation_image_h2/ae84dd6c8150ce1e201ed72c26554d81/image-2.jpg)
Bayes’ Theorem If Pr[y] > 0 then Pr[x|y] = Pr[x]Pr[y|x]/ x X Pr[x]Pr[y|x] What is the probability that the 1 st dice throw is 2 when the sum of two dice throws is 5? What is the probability that the 2 nd dice throw is 3 when the product of the two dice throws is: 6, and 5? 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 2

(Im)Perfect Secrecy: Example P = {1, 2, 3} K = {K 1, K 2, K 3} and C = {2, 3, 4, 5, 6} K 1 K 2 K 3 1 2 3 4 5 6 Keys chosen equiprobably Pr[1] = Pr[2] = Pr[3] = 1/3 Pr[c=3] = ? Pr[m|c=3] = ? Pr[k|c=3] = ? 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 3
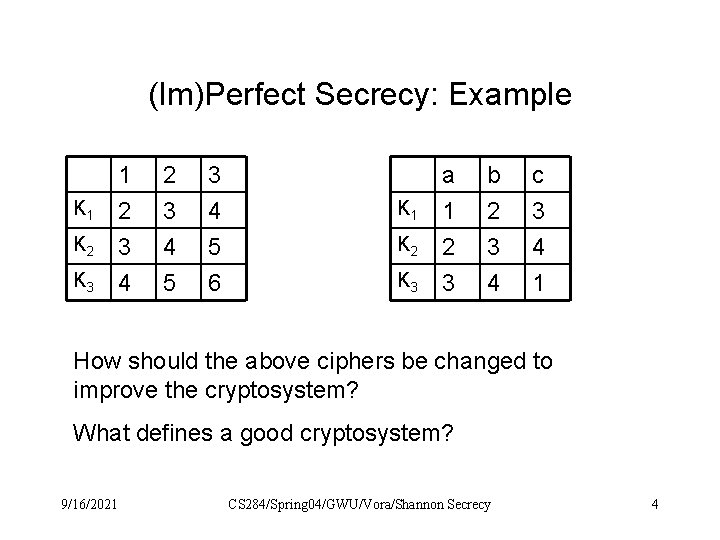
(Im)Perfect Secrecy: Example K 1 K 2 K 3 1 2 3 4 5 6 K 1 K 2 K 3 a 1 2 3 b 2 3 4 c 3 4 1 How should the above ciphers be changed to improve the cryptosystem? What defines a good cryptosystem? 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 4
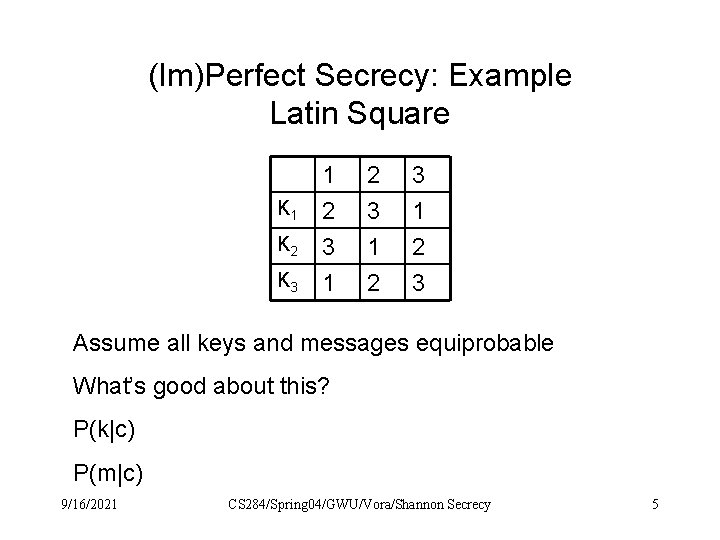
(Im)Perfect Secrecy: Example Latin Square K 1 K 2 K 3 1 2 3 Assume all keys and messages equiprobable What’s good about this? P(k|c) P(m|c) 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 5
![Perfect Secrecy: Definition A cryptosystem has perfect secrecy if Pr[x|y] = Pr[x] x P, Perfect Secrecy: Definition A cryptosystem has perfect secrecy if Pr[x|y] = Pr[x] x P,](http://slidetodoc.com/presentation_image_h2/ae84dd6c8150ce1e201ed72c26554d81/image-6.jpg)
Perfect Secrecy: Definition A cryptosystem has perfect secrecy if Pr[x|y] = Pr[x] x P, y C a posteriori probability = a priori probability posterior = prior 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 6

Example: one-time pad P = C = Z 2 n d. K=e. K(x 1, x 2, …xn) = (x 1+K 1, x 2+K 2, …xn+Kn) mod 2 Show that it provides perfect secrecy 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 7

Some proofs: Thm. 2. 4 Thm 2. 4: Suppose (P, C, K, E, D) is a cryptosystem where |K| = |P| = |C|. Then the cryptosystem provides perfect secrecy if and only if every key is used with equal probability 1/|K|, and x P and y C, there is a unique key K such that e. K(x) = y (eg: Latin square) 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 8

Entropy H(X) = - pi log 2 pi Example: pi = 1/n Examples: ciphertext and plaintext entropies for examples. 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 9

Huffman encoding f: X* {0, 1}* String of random variables to string of bits e. g. X = {a, b, c, d} f(a) = 1, f(b) = 10, f(c) = 100, f(d) = 1000 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 10

Huffman encoding algorithm X = {a, b, c, d, e} p(a) = 0. 05 p(b) = 0. 1 p(c) = 0. 12 p(d) = 0. 13 p(e) = 0. 6 a: 000, b: 001, c: 010, d: 011, e: 1 9/16/2021 a b c d e 0. 05 0. 12 0. 13 0. 6 0 1 0. 15 0. 25 0 1 0. 4 0 0. 6 1 Average length = ? Entropy = ? CS 284/Spring 04/GWU/Vora/Shannon Secrecy 11

Theorem H(X) average length of Huffman encoding H(X) + 1 Without proof 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 12

Properties of Entropy H(X) log 2 n • H(X, Y) H(X) + H(Y) • H(X, Y) = H(X) + H(Y|X) = H(Y) + H(X|Y) Where H(X|Y) = - x y p(y)p(x|y)log 2 p(x|y) • H(X|Y) H(X) • With proofs and examples 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 13

Theorem H(K|C) = H(K) + H(P) – H(C) Examples: Previous imperfect squares Proof: H(K, P, C) = H(K, P) 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 14

Language Entropy and Redudancy HL = Lim n H(Pn ) /n (lies between 1 and 1. 5 for English) RL = 1 – HL /log 2 |P| (the amount of “space” in a letter of English for other information) Need, on average, about n ciphertext characters to break a substitution cipher where: n = key entropy / RL log 2 |P| n is “unicity distance” of cryptosystem 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 15

Proof • H(K|Cn) = H(K) + H(Pn) – H(Cn) 9/16/2021 CS 284/Spring 04/GWU/Vora/Shannon Secrecy 16
- Slides: 16