Probability Revisited Austin Cole Outline Expectation Variance Distributions

Probability Revisited Austin Cole

Outline • Expectation & Variance • Distributions – Bernoulli – Binomial – Geometric – Negative Binomial – Hypergeometric – Poisson

Probability Basics • Probability Mass Function (PMF): function that gives the probability that a discrete random variable is equal to some value, f(x)=P[X = x] • Cumulative Distribution Function (CDF): a function F(x)=P[X ≤ x] • For continuous r. v. , f(x)=F´(x)

Expectation • E[X]: What you expect the average for X to be in the long run • Also known as weighted average, population mean or μ

• An urn contains 3 red balls and 4 blue balls. Balls are drawn at random without replacement. Let the random variable X be the trial # when the 1 st red ball is drawn. Find E[X]

Variance • σ2=Var(X)=E[X 2] – (E[X]) 2 • The square of the standard deviation σ of X • How to calculate E[X 2]? • E[X 2]=Σx 2 f(x) or ʃx 2 f(x)dx

Bernoulli Distribution • K=1 signifies ‘success’, K=0 represents failure • Whether a coin comes up heads • What is f(x)?

Bernoulli Distribution • E[X]=p • V[X]=p(1 -p) • Special case of p=1/2 – μ=1/2 – V[X]=1/4 *largest possible variance for Bernoulli r. v. – The PMF has the widest peak about the mean of any r. v.

Binomial Distribution • • Consists of n identical trials There are two possible outcomes Trials are mutually independent Probability of each success on each trial is the same • f(X=k)=

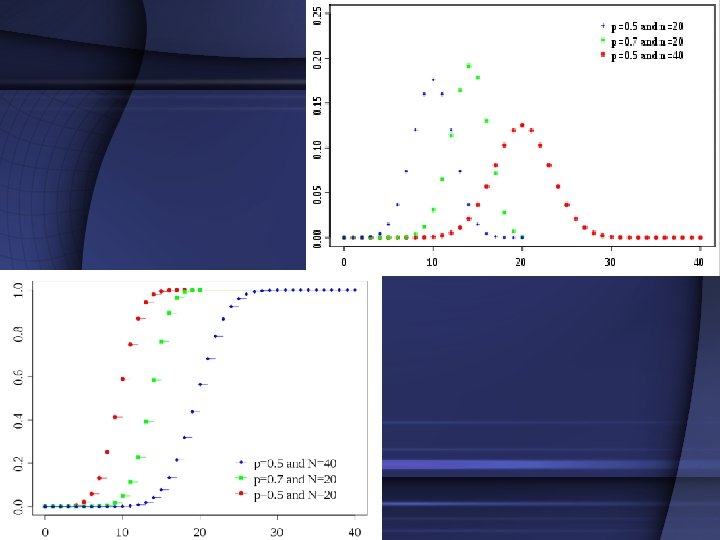
Binomial Distribution • E[X]=np • V[X]=np(1 -p) • Example: Defective eggs

• A dozen eggs contains 3 defectives. If a sample of 5 is taken with replacement, find the probability that exactly 2 of the eggs sampled are defective. Also, find the probability that 2 or fewer are defective. • n=5; p=1/4 5 • f(x)=( x )(1/4) x(3/4) 5 -x • Exercise 1

Geometric Distribution • Probability that the first success comes on the kth trial • f(X=k)=(1 -p) k-1 p • E[X]=(1 -p)/p • V[X]=(1 -p)/p 2 • Memoryless

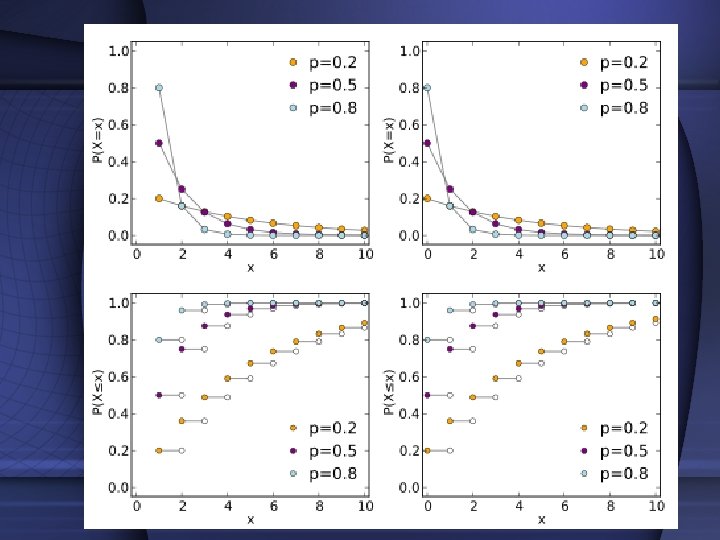
Example • Suppose the probability of an engine malfunction for any one-hour period is p=. 02. Find the probability that a given engine will survive 2 hours. • P[survive 2 hrs]=1 -P[x<2] =1 -(. 98)1 -1(. 02)-(. 98) 2 -1(. 02) =. 9604

Negative Binomial Distribution • Probability of having k successes and r failures • E[X]=k(1 -p)/p • V[X]= k(1 -p)/p 2 • f(X=k)= k

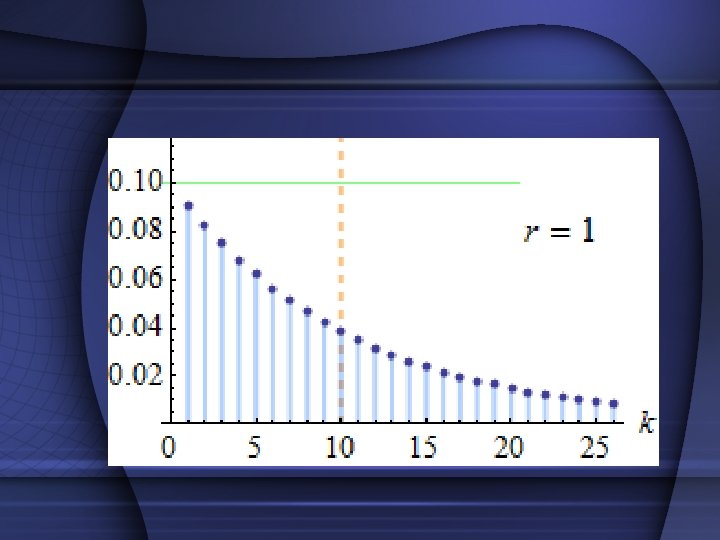
Exercise 2 • A geological study indicates that an exploratory oil well drilled in a particular region should strike oil with probability p=. 2. Find the probability that the 3 rd oil strike comes on the 5 th well drilled.

Hypergeometric Distribution • Probability of sampling involving N items without replacement • f(X=k)= • m successes, N-m failures • E[X]=nm/N m m N-n • V[X]=n*(--)*(1 --)*(----) N N N-1

Example • A biologist uses a “catch & release” program to estimate the population size of a particular animal in a region. During the catch phase, 20 animals are tagged. Months later, 30 animals are captured, and 7 have tags.

Poisson Distribution • Often used for large n and small p • E[X]=λ • V[X]= λ • f(X=k)=

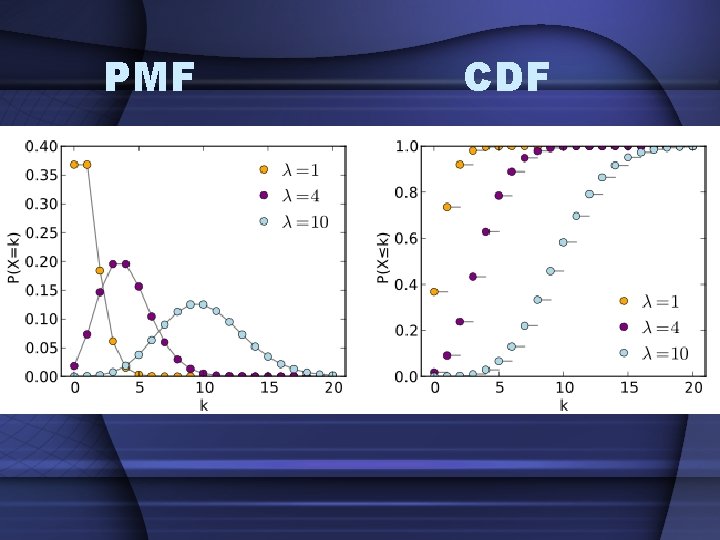
PMF CDF

A closer look at Poisson • Suppose we want to find the probability distribution of the number of accidents at an intersection during the time period of one week • Divide the week into subintervals so: – P[no accident in subinterval]=1 -p – P[1 accident in subinterval]=p – P[2+ accidents in subinterval]=0

• Occurrence of accidents can be assumed to be independent from interval to interval (X~Bin(n, p)) • X=total # of subintervals w/ an accident • Let p=λ/n λ 2 λ n-x -λ)*(λx)/x! • ( nx )(--) (1 --) = (e n n

Poisson Example • A rare disease affects. 2% of the population. Find the probability that city A of 500, 000 has 1, 040 or fewer people infected. 1040 x). 998 500000 -x • P(X≤ 1040)=Σ( 500000 )(. 002 x X=0 1040 • P(X≤ 1040)=Σ X=0 1000 x e-1000 ------x! ≈. 8995

Discussion • Are there any other uses that you see for probability? • Have you used basic knowledge for probability in certain situations?