Probability Reliability Practice2 Additional chapters of mathematics Dmitriy

Probability, Reliability Practice-2 Additional chapters of mathematics Dmitriy Sergeevich Nikitin Assistant Tomsk Polytechnic University email: Nikitin. Dm. Sr@yandex. ru 1

Law of total probability The law (formula) of total probability is a consequence of both the main theorems: the addition theorem for probabilities and theorem of multiplication of probabilities. It is required to determine the probability of some event A, which can occur together with one of the events: H 1, H 2, …, Hn, forming a complete group of inconsistent events. We call these events hypotheses. 2

Law of total probability 3

Law of total probability 4

Task 1 There are three lightning discharges along the power transmission line. The probability of striking: - in the first lightning in the power line is 0. 4; - in the second lightning in the power line is 0. 5; - in the third lightning in the power line is 0. 7. The line fails - with a probability of 0. 2 when one lightning discharge strikes; - with a probability of 0. 6 when two lightning discharges strike; - with a probability of 1. 0 when three lightning discharges strike. Find the probability of line failure as a result of lightning discharges. 5

The hypothesis theorem (Bayes formula) A consequence of the multiplication theorem and the formula of total probability is theorem of hypotheses, or the Bayes formula. There is a complete group of disjoint hypotheses H 1, H 2, …, Hn. The probabilities of these hypotheses before the experiment are known and are equal to P(H 1), P(H 2), …, P(Hn), respectively. An experiment was made, as a result of which event A took place. How should the probabilities of hypotheses be changed in connection with the appearance of this event? 6

The hypothesis theorem (Bayes formula) 7

Task 2 The cable that feeds the transformer substation operates in two modes: a) nominal; b) with overload. The duration of the first mode is 80 % of the operating time, The duration of the first mode is 20 % of the operating time. The probability of the cable’s failure during the time t in the nominal mode is 0. 1; in the overload mode is 0, 7. To find: 1. The probability of the cable’s failure during the time t. 2. The cable is faulty. What is the probability that it has failed, working in the first mode? 8

Reliability indicators 9

Reliability indicators 10

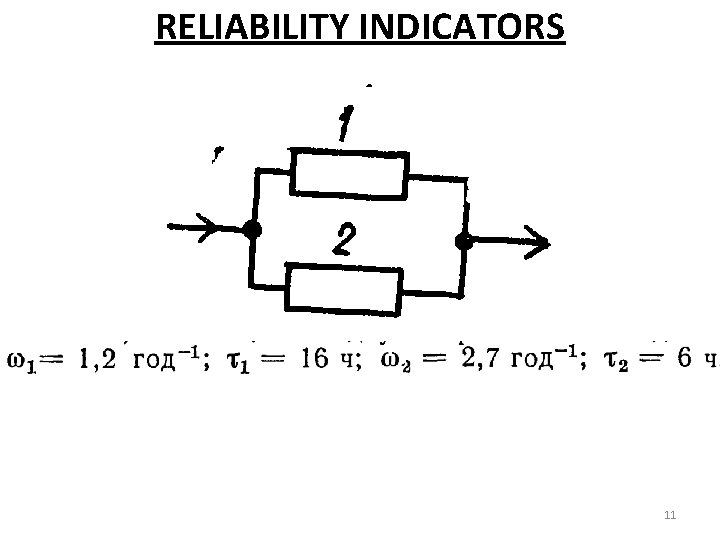
RELIABILITY INDICATORS 11