PROBABILITY RANDOM EXPERIMENTS PROBABILITY OF OUTCOMES EVENTS PROBABILITY

PROBABILITY • RANDOM EXPERIMENTS • PROBABILITY OF OUTCOMES • EVENTS • PROBABILITY OF EVENTS

RANDOM EXPERIMENTS • IF WE CANNOT FORSEE THE OUTCOME OF AN EXPERIMENT IT IS SAID TO BE RANDOM • SET OF POSSIBILITIES (UNIVERSAL SET) IS THE SET OF ALL POSSIBLE OUTCOMES REPRESENTED BY THE SYMBOL Ω ex. Roll the die once - Ω = 1, 2, 3, 4, 5, 6 Venn Diagram 1 4 3 6 5 2 Ω

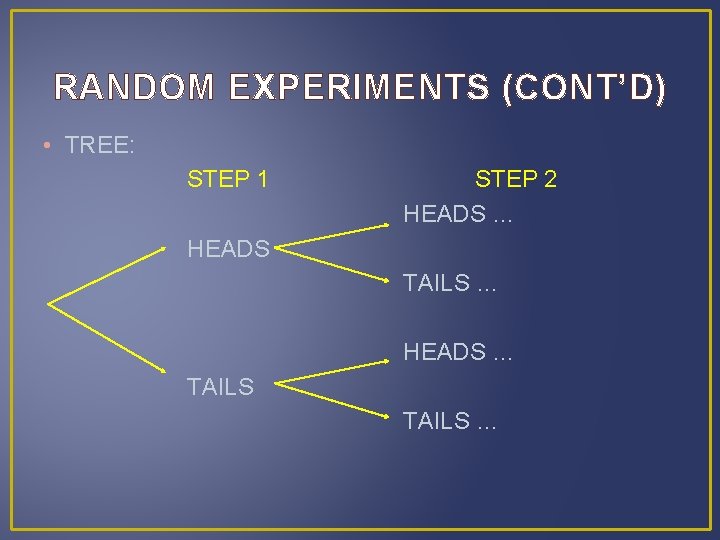
RANDOM EXPERIMENTS (CONT’D) • TREE: STEP 1 STEP 2 HEADS … HEADS TAILS … HEADS … TAILS …

RANDOM EXPERIMENTS (CONT’D) • BASIC COUNTING RULE: • EXPERIMENTS INVOLVING 2 STEP: If the first step can be counted in a ways and the second step can be accomplished in b ways, then the total number of possible outcomes for this experiment is equal to the product axb • EXPERIMENTS INVOLVING 3 STEPS: If the third step can be accomplished in c ways then axbxc • Ex. If Eric has 2 pairs of pants (one black, one grey), 3 shirts (one white, one blue, one red), and 2 ties (one yellow, one red) 2 x 3 x 2 = 12 possible combinations

PROBABILITY OF AN OUTCOME •

PROBABILITY OF AN OUTCOME •

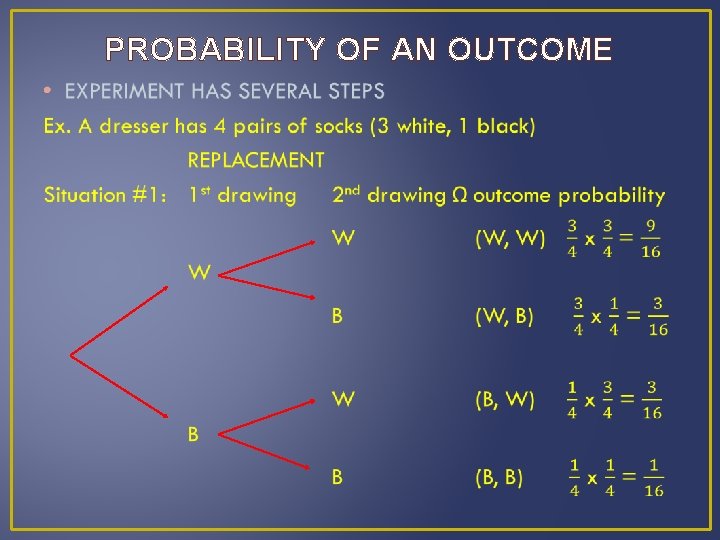
PROBABILITY OF AN OUTCOME •

PROBABILITY OF AN OUTCOME •

EVENTS •

EVENTS • INCOMPATIBLE EVENTS – mutually exclusive events that cannot occur simultaneously. Ex. You cannot draw both a Spade and a Heart • COMPLIMENTARY EVENTS – (contrary) if two events are incompatible AND if it is certain that either of these events will occur Ex. Rolling an ODD number or rolling an EVEN number.

PROBABILITY OF AN EVENT • 4 5 1 10 2 2 3 3

PROBABILITY OF AN EVENT • DEPENDENT AND INDEPENDENT EVENTS • INDPENDENT – occurs when one event does not influence the probability of the other occurring. Ex. Pulling a card from the deck and replacing it. You are choosing from a 52 card deck every time. • DEPENDENT – occurs when one event influences the probability of the other occurring. Ex. Pulling a card from a deck and NOT replacing it. You are choosing from a decreasing number of cards each time.