Probability Mutually Exclusive Events which can not occur

Probability Mutually Exclusive – Events which can not occur at the same time Non Mutually Exclusive – Events which can occur at the same time Independent – The occurrence of one event does not effect the other Dependent – The occurrence of one event does effect the other
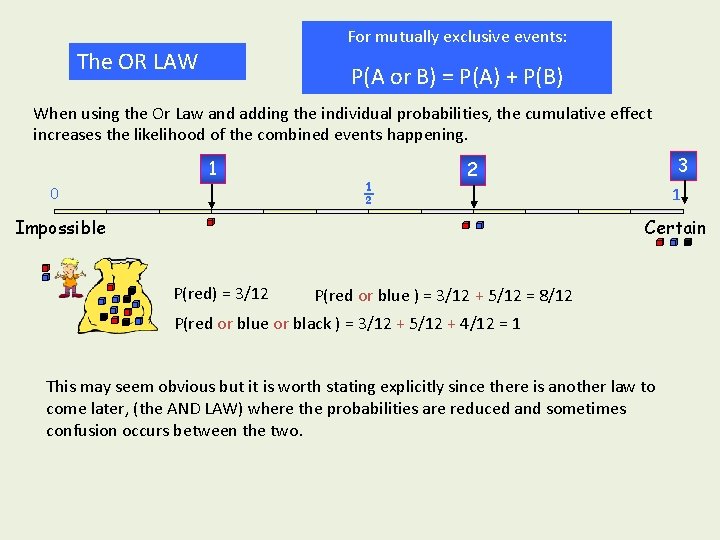
For mutually exclusive events: The OR LAW P(A or B) = P(A) + P(B) When using the Or Law and adding the individual probabilities, the cumulative effect increases the likelihood of the combined events happening. 1 0 ½ 3 2 1 Certain Impossible P(red) = 3/12 P(red or blue ) = 3/12 + 5/12 = 8/12 P(red or blue or black ) = 3/12 + 5/12 + 4/12 = 1 This may seem obvious but it is worth stating explicitly since there is another law to come later, (the AND LAW) where the probabilities are reduced and sometimes confusion occurs between the two.

Events that are NOT Mutually Exclusive If the events in question are not mutually exclusive then the OR LAW cannot be used and the probabilities cannot be added. Consider the problem of taking a card at random from a pack. What is the probability of selecting a diamond or a queen? These events are not mutually exclusive because the queen of diamonds is both a queen and a diamond.
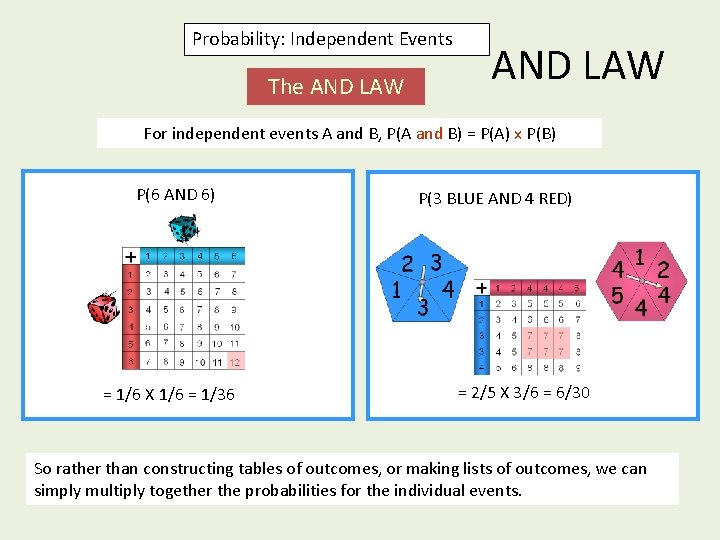
Probability: Independent Events The AND LAW For independent events A and B, P(A and B) = P(A) x P(B) P(6 AND 6) = 1/6 X 1/6 = 1/36 P(3 BLUE AND 4 RED) = 2/5 X 3/6 = 6/30 So rather than constructing tables of outcomes, or making lists of outcomes, we can simply multiply together the probabilities for the individual events.

The AND LAW For mutually exclusive events: P(A and B) = P(A) x P(B) When using the And Law and multiplying the individual probabilities, the cumulative effect decreases the likelihood of the combined events happening. 3 2 1 ½ 0 1 Certain Impossible P(6) = 1/6 P(double 6) = 1/36 Common sense should tell you that it is much harder (less likely) to throw a double six with two dice, then it is to throw a single 6 with one die. What do you think the probability of getting a triple 6 with a throw of 3 dice might be? P(triple 6) 1/6 x 1/6 = 1/216

. Rebecca has nine coloured beads in a bag. Four of the beads are red and the rest are blue. She removes a bead at random from the bag and notes the colour before replacing it. She then chooses a second bead. Calculate the probability that Rebecca chooses: (a) 2 red beads (b) A blue followed by a red bead. (a) P(red and red) = (b) P(blue and red) = 4/9 x 4/9 = 16/81 5/9 x 4/9 = 20/81 Beads
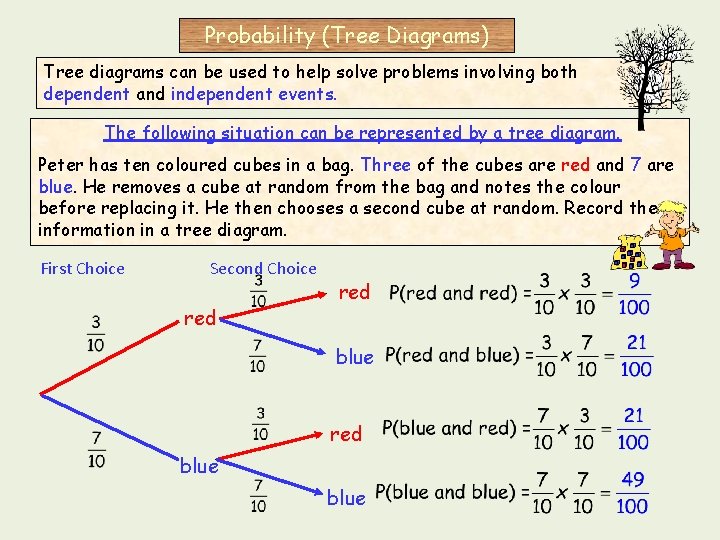
Probability (Tree Diagrams) Tree diagrams can be used to help solve problems involving both dependent and independent events. The following situation can be represented by a tree diagram. Peter has ten coloured cubes in a bag. Three of the cubes are red and 7 are blue. He removes a cube at random from the bag and notes the colour before replacing it. He then chooses a second cube at random. Record the information in a tree diagram. First Choice Second Choice red blue

Probability (Tree Diagrams) Q 3 Sports Question 3 Peter and Becky run a race and play a tennis match. The probability that Peter wins the race is 0. 4. The probability that Becky wins the tennis is 0. 7. (a) Complete the tree diagram below. (b) Use your tree diagram to calculate (i) the probability that Peter wins both events. (ii) The probability that Becky loses the race but wins at tennis. Tennis 0. 3 Race 0. 4 Peter Win 0. 7 0. 3 0. 6 Becky Win 0. 7 P(Win and Win) for Peter = 0. 12 Peter Win 0. 4 x 0. 3 = 0. 12 Becky Win 0. 4 x 0. 7 = 0. 28 Peter Win 0. 6 x 0. 3 = 0. 18 Becky Win 0. 6 x 0. 7 = 0. 42 P(Lose and Win) for Becky = 0. 28
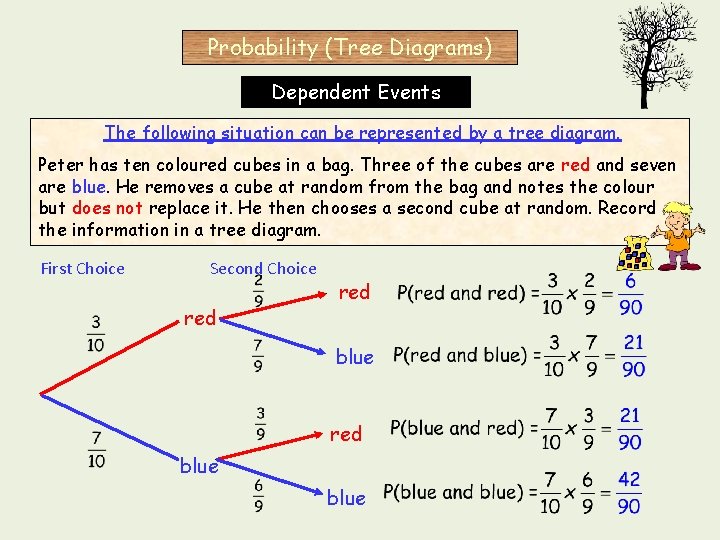
Probability (Tree Diagrams) Dependent Events The following situation can be represented by a tree diagram. Peter has ten coloured cubes in a bag. Three of the cubes are red and seven are blue. He removes a cube at random from the bag and notes the colour but does not replace it. He then chooses a second cube at random. Record the information in a tree diagram. First Choice Second Choice red blue
- Slides: 9