Probability matrices and game theory The mathematics of

Probability, matrices and game theory The mathematics of Blackjack (21)

Basic Idea • Draw cards to get as close as possible to a total of 21 without going over PLAYER DEALER Highest total wins!

Complications of Blackjack • • Ace = 1 or 11 Blackjack (Ace+Ten) vs. 21 Splitting pairs Doubling down Insurance When cards are shuffled Whose cards you can see Casino-dependent special cases

Decimal Blackjack (Version 1. 0) • Remove all the face-cards; let Ace=1 • Each number from 1 to 10 occurs with equal probability of 0. 1 • One card each: high card wins Not very exciting. . . no decisions to make

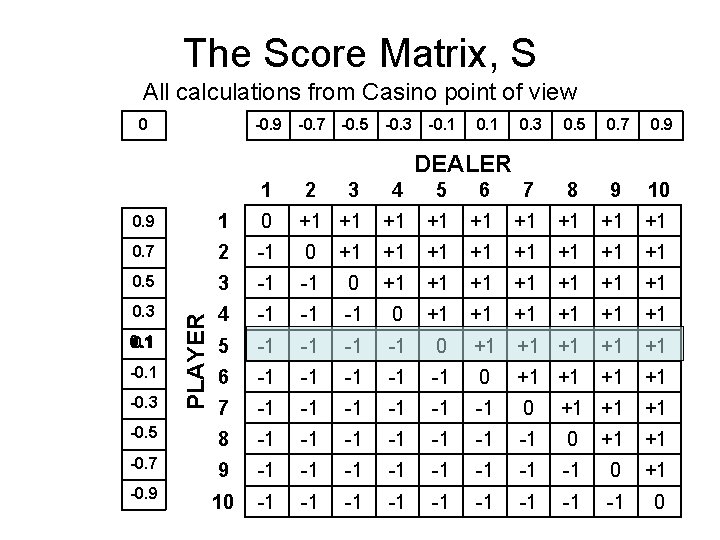
The Score Matrix, S All calculations from Casino point of view 0 -0. 9 -0. 7 -0. 5 -0. 3 -0. 1 0. 3 0. 5 0. 7 0. 9 DEALER 1 2 3 4 5 6 7 8 9 10 1 0 +1 +1 +1 0. 7 2 -1 0 +1 +1 0. 5 3 -1 -1 0 +1 +1 0. 3 4 -1 -1 -1 0 +1 +1 +1 5 -1 -1 0 +1 +1 +1 6 -1 -1 -1 0 +1 +1 7 -1 -1 -1 0 +1 +1 +1 -0. 5 8 -1 -1 0 +1 +1 -0. 7 9 -1 -1 0 +1 -0. 9 10 -1 -1 -1 0 0. 1 -0. 3 PLAYER 0. 9

Score matrix, expectations and game value • Score matrix, S • Card probability vector p = (0. 1, 0. 1 , 0. 1, 0. 1) • Player expectations • Dealer expectations • Expected game value

Score matrix, expectations and game value Blackjack 1. 0

Decimal Blackjack (Version 1. 1) • Player (only) has option to HIT – drawing additional cards to improve total before seeing Dealer’s card – must not go over 10. PLAYER DEALER

Decimal Blackjack (Version 1. 1) PLAYER DEALER

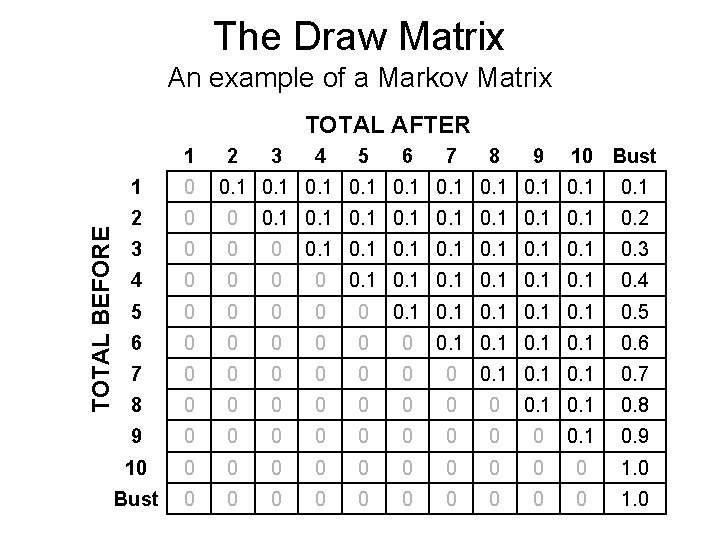
The Draw Matrix An example of a Markov Matrix TOTAL AFTER 1 2 3 4 5 6 7 8 9 10 Bust 0 2 0 0 3 0 0 0 4 0 0 5 0 0 0 6 0 0 0 7 0 0 0 0 8 0 0 0 0 9 0 0 0 0 0. 1 0. 9 10 0 0 1. 0 Bust 0 0 0 0 0 1. 0 TOTAL BEFORE 1 0. 1 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6 0. 7 0. 8

Draw Matrix, D

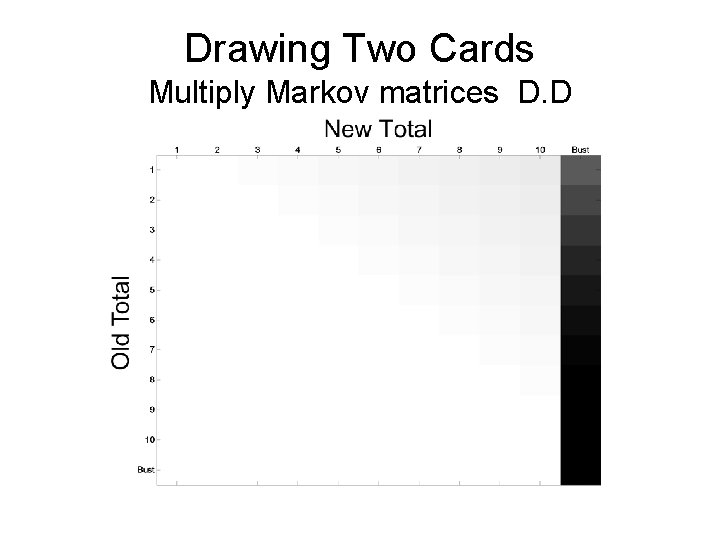
Drawing Two Cards Multiply Markov matrices D. D

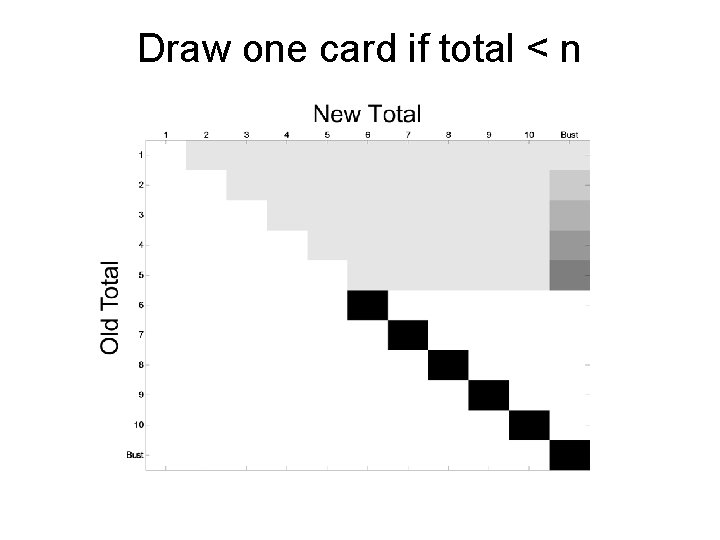
Draw one card if total < n

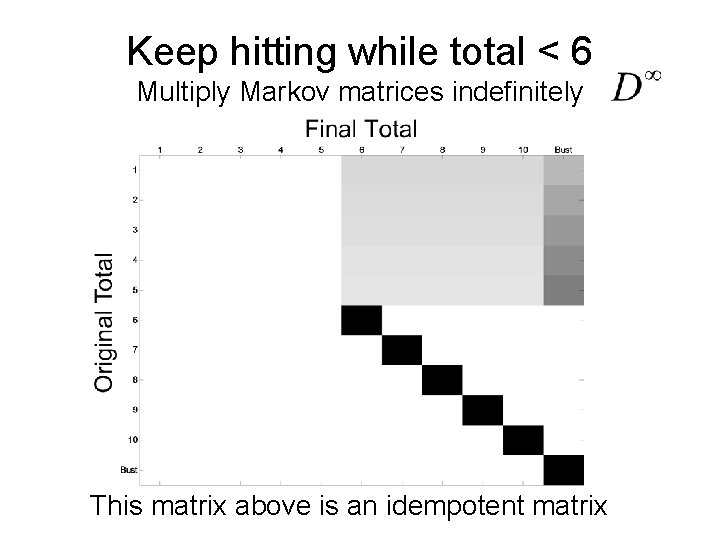
Keep hitting while total < 6 Multiply Markov matrices indefinitely This matrix above is an idempotent matrix

Score matrices for Decimal Blackjack 1. 1 • Player’s drawing Markov matrix, D • Score matrix • Player expectations • Dealer expectations • Expected game value

Blackjack 1. 1: Player hits when < 6

Blackjack 1. 1: Player hits when < 5

Blackjack 1. 1: Player hits when < 4

Summary: Blackjack 1. 1 • Player hits when total n is – – – n<1, zero advantage (same as dealer strategy) n<2, 8. 45% advantage n<3, 14. 67% advantage n<4, 21. 1% advantage n<5, 22. 98% advantage (OPTIMAL STRATEGY) n<6, 20. 79% advantage n<7, 13. 38% advantage n<8, 6. 2% disadvantage n<9, 22. 83% disadvantage n<10, 55. 2% disadvantage n<11, 100% disadvantage

Decimal Blackjack (Version 1. 2) • Both player and dealer can HIT – but let’s assume for now that whoever goes second cannot see the first player’s cards (Las Vegas style Blackjack) PLAYER DEALER

Scoring for Decimal Blackjack 1. 2 • Player’s Markov matrix • Dealer’s Markov matrix • Expected game value

Game Matrix Compare opposing strategies Player Strategies Dealer Strategies hit when n<4 n<5 n<6 n<7 n<8 n<4 0 6. 4% 8. 8% 6. 0% -3. 6% n<5 -6. 4% 0 4. 5% 3. 8% -3. 7% n<6 -8. 8% -4. 5% 0 1. 8% -3. 2% n<7 -6. 0% -3. 8% -1. 8% 0 -2. 0% n<8 3. 6% 3. 7% 3. 2% 2. 0% 0 • For any given dealer strategy, player would choose the row which gives the MINIMUM • For any given player strategy, dealer would choose the column which gives the MAXIMUM

Saddle-points • An entry in the game matrix which is a minimum in its column and a maximum in its row is called a Saddle Point • Pairs of strategies that form saddle points are “optimal” and in “equilibrium”: neither person has an incentive to play differently

Decimal Blackjack 1. 2 • Both player and dealer should choose the strategy – HIT on all totals less than 7

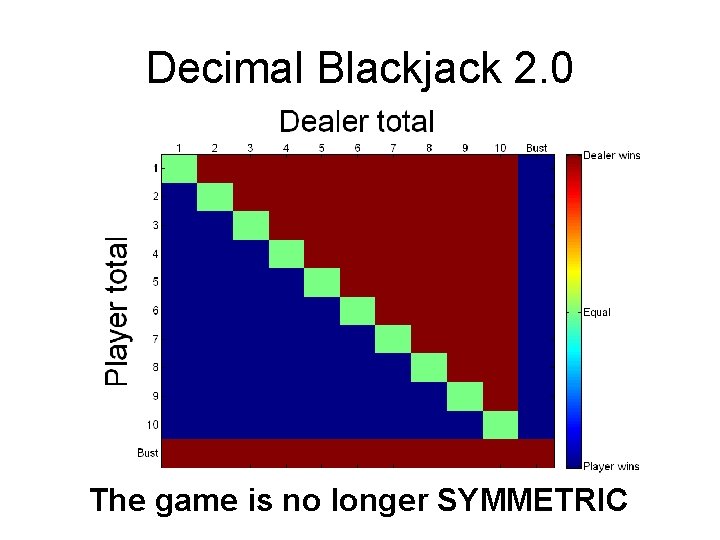
Decimal Blackjack 2. 0 The game is no longer SYMMETRIC

Game Matrix for Version 2. 0 Player Strategies Dealer Strategies hit when n<4 n<5 n<6 n<7 n<8 n<4 4. 7% 7. 2% 10. 1% 8. 0% -0. 7% n<5 -5. 5% 1. 4% 6. 8% 7. 3% 1. 3% n<6 -7. 5% -2. 1% 3. 8% 7. 4% 4. 9% n<7 -4. 0% -0. 2% 3. 9% 8. 5% 10. 1% n<8 6. 4% 8. 8% 11. 3% 14. 2% 17. 2% • MINIMUM entry in each column • MAXIMUM entry in each row • There is a Saddle-point

Optimal strategies for Decimal Blackjack 2. 0 • Dealer should HIT if total < 7 • Player should HIT if total < 5 • Advantage to Casino = 7. 3%

Game Matrix for Version 2. 1 New goal: Closest to 21 without busting Player Strategies Dealer Strategies hit when n<14 n<15 n<16 n<17 n<18 n<14 2. 6% 12. 8% 18. 7% 17. 5% 9. 1% n<15 -11. 8% 1. 1% 10. 7% 13. 2% 8. 3% n<16 -16. 9% -7. 1% 3. 1% 9. 7% 8. 9% n<17 -14. 8% -7. 7% -0. 3% 7. 1% 10. 8% n<18 -5. 3% -0. 5% 4. 4% 9. 3% 14. 3% • MINIMUM entry in each column • MAXIMUM entry in each row • There is NO saddle-point! NO equilibrium!

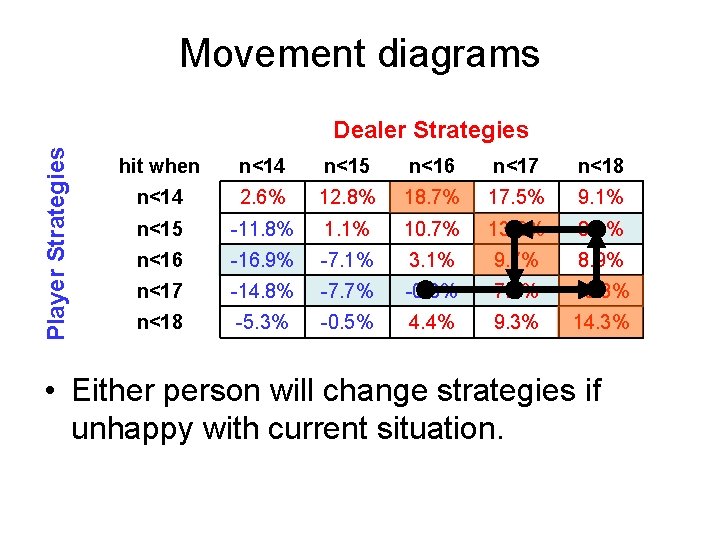
Movement diagrams Player Strategies Dealer Strategies hit when n<14 n<15 n<16 n<17 n<18 n<14 2. 6% 12. 8% 18. 7% 17. 5% 9. 1% n<15 -11. 8% 1. 1% 10. 7% 13. 2% 8. 3% n<16 -16. 9% -7. 1% 3. 1% 9. 7% 8. 9% n<17 -14. 8% -7. 7% -0. 3% 7. 1% 10. 8% n<18 -5. 3% -0. 5% 4. 4% 9. 3% 14. 3% • Either person will change strategies if unhappy with current situation.

Mixed Strategies Player Strategies Dealer Strategies hit when n<17 29% n<17 and 71% n<18 n<15 13. 2% 9. 7% 8. 3% 43% n<15 and 57% n<17 9. 7% n<17 7. 1% 9. 7% 10. 8% n<18 • Randomly change between 2 or more different strategies

Minimax theorem Every two-person zero-sum game with a finite number of pure strategies has a minimax equilibrium if mixed strategies are allowed Borel, Fisher, Von Neumann, Morgenstern, Nash proved in a various ways between 1920 and 1950

Blackjack 2. 13 • Let’s put the face cards back in the deck – Face cards count as 10 • Probability distribution is now

Game Matrix for Version 2. 13 Player Strategies Dealer Strategies hit when n<14 n<15 n<16 n<17 n<18 n<14 0. 8% 6. 9% 9. 2% 7. 2% 0. 7% n<15 -4. 3% 2. 2% 6. 9% 7. 4% 3. 3% n<16 -5. 2% -0. 2% 5. 0% 8. 2% 6. 9% n<17 -1. 7% 2. 0% 5. 8% 9. 8% 11. 5% n<18 6. 6% 9. 1% 11. 7% 14. 4% 17. 2% • Both player and dealer want to HIT less often when the proportion of 10’s are higher. • Mixed equilibrium has dealer advantage of 7. 6%

Effect of card distribution • Blackjack 2. 10 – Dealer advantage 9. 7% – Dealer mixes hitting with n<17 and n<18 – Player mixes hitting with n<15 and n<17 • Blackjack 2. 13 – Dealer advantage 7. 6% – Dealer mixes hitting with n<16 and n<17 – Player mixes hitting with n<14 and n<16

Blackjack 3. 0 • In legal casinos the dealer plays a fixed and publicly known strategy! • Let’s FIX this strategy to be HIT if n<17 • This is the best FIXED strategy for the casino with an initial distribution

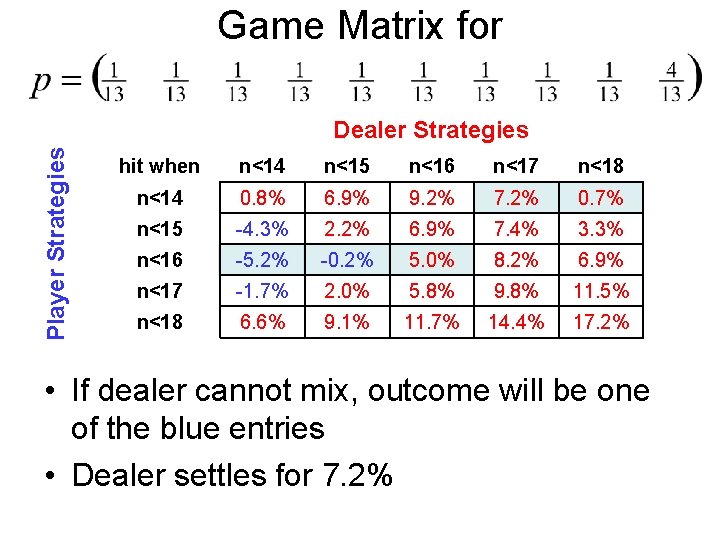
Game Matrix for Player Strategies Dealer Strategies hit when n<14 n<15 n<16 n<17 n<18 n<14 0. 8% 6. 9% 9. 2% 7. 2% 0. 7% n<15 -4. 3% 2. 2% 6. 9% 7. 4% 3. 3% n<16 -5. 2% -0. 2% 5. 0% 8. 2% 6. 9% n<17 -1. 7% 2. 0% 5. 8% 9. 8% 11. 5% n<18 6. 6% 9. 1% 11. 7% 14. 4% 17. 2% • If dealer cannot mix, outcome will be one of the blue entries • Dealer settles for 7. 2%

Game Matrix for Player Strategies Dealer Strategies hit when n<14 n<15 n<16 n<17 n<18 n<14 2. 6% 12. 8% 18. 7% 17. 5% 9. 1% n<15 -11. 8% 1. 1% 10. 7% 13. 2% 8. 3% n<16 -16. 9% -7. 1% 3. 1% 9. 7% 8. 9% n<17 -14. 8% -7. 7% -0. 3% 7. 1% 10. 8% n<18 -5. 3% -0. 5% 4. 4% 9. 3% 14. 3% • Out of all fixed strategies dealer would prefer to settle for n<18 with 8. 3% • Legal casino dealers can’t change strategies based on p so must play n<17 and get only 7. 1%

Blackjack 3. 0 with card counting and fixed dealer strategy n<17 – Hit with n<14 (dealer advantage 7. 2%) – Hit with n<17 (dealer advantage 7. 1%) – Hit with n<18 (player advantage 4. 3%) – Hit with n<12 (player advantage 27%)

Blackjack 4. 0 Can see the dealer’s first card • Instead of using a game value of use instead

Strategy for Blackjack 4. 0 can see the dealer’s first card • • • Dealer shows 1, HIT if n < 14 (Dealer advantage 11. 0%) Dealer shows 2, HIT if n < 13 (Player advantage 1. 0%) Dealer shows 3, HIT if n < 13 (Player advantage 3. 7%) Dealer shows 4, HIT if n < 12 (Player advantage 6. 6%) Dealer shows 5, HIT if n < 12 (Player advantage 9. 6%) Dealer shows 6, HIT if n < 12 (Player advantage 12. 7%) Dealer shows 7, HIT if n < 17 (Player advantage 3. 7%) Dealer shows 8, HIT if n < 17 (Dealer advantage 3. 2%) Dealer shows 9, HIT if n < 17 (Dealer advantage 11. 2%) Dealer shows 10, HIT if n<16 (Dealer advantage 21. 6%) Overall dealer advantage 5. 7%

Real Blackjack factoids • Optimal non-card-counting strategy – 1 -deck game Player advantage 0. 04% – 4 -deck game Dealer advantage 0. 49% – Infinite decks Dealer advantage 0. 65% • Observation in 1987 of 11, 000 actual hands played in Nevada/New Jersey – Non-optimal average-Joe play Dealer advantage 2% – Players who tried to count cards made a mistake once every 7 hands Dealer advantage 9%