Probability MATHSWATCH CLIP 14 59 60 125 GRADE

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 L. O. To be able to § Place outcomes on a probability scale § Write probabilities using fractions or decimals Key Words event, outcome, scale, certain, impossible, likely, unlikely

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 https: //www. youtube. com/watch? v=ur_h. Hj. Lr. BNo&feature=emb_logo Probability

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 LANGUAGE OF PROBABILITY
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Discussion Think of an example sentence which contains each of the following probability words unlikely possible probable 50 -50 chance certain even chance likely poor chance very likely impossible

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Discussion In which scenarios does each outcome have an equal chance of occurring? § It will rain tomorrow. § A child born will be a boy. § A coin will show tails when it is flipped. § A number selected at random from 1 to 100 will be even. § When a dice is thrown, it will show a square number. § The next person to walk into the room will be right handed. § The bus will be on time tonight. § The bus driver will be female. § When a dice is thrown, it will show a prime number.

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Discussion Do you agree or disagree with the following statements? The number 18 has been drawn the most often in the national lottery so I’m more likely to win if I choose it. I’m so unlucky. If I roll this dice I’ll never get a six. I’ve just thrown four heads in a row so I’m much less likely to get a head on my next throw. There are two choices for lunch, pizza or curry. That means that there is a 50% chance that the next person will choose pizza.

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 THE PROBABILITY SCALE
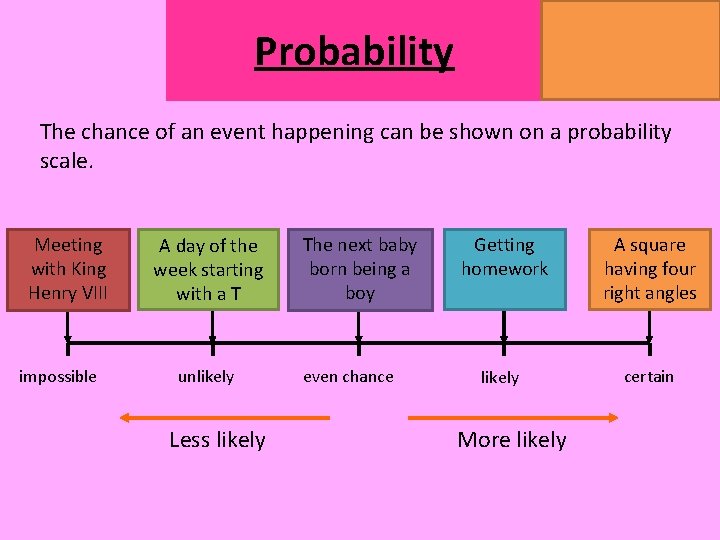
MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability The chance of an event happening can be shown on a probability scale. Meeting with King Henry VIII impossible A day of the week starting with a T unlikely Less likely The next baby born being a boy even chance Getting homework A square having four right angles likely certain More likely
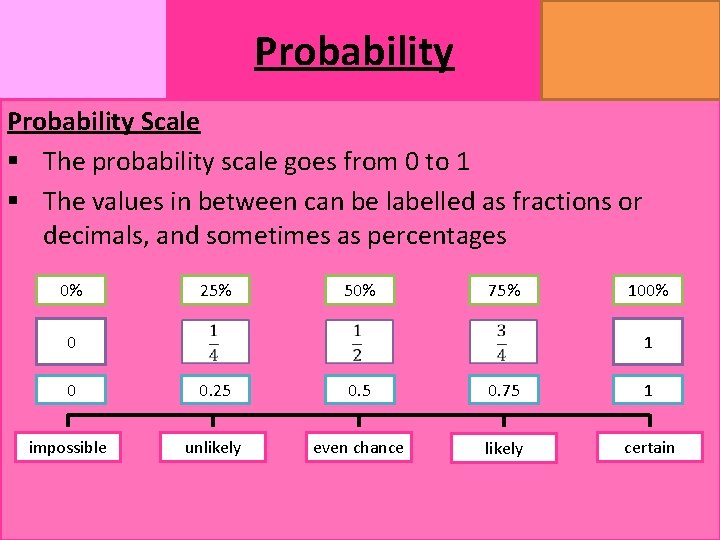
MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Scale § The probability scale goes from 0 to 1 § The values in between can be labelled as fractions or decimals, and sometimes as percentages 0% 25% 50% 75% 0 100% 1 0 0. 25 0. 75 1 impossible unlikely even chance likely certain

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Example Work out where these events would go on the probability scale below 0 3 2 4 ½ 5 1 4 Choosing a red cube at random from the bag. 1 Certain Impossible 1 Getting a tail when tossing a coin. 6 2 Getting a 3 when you throw a die. 3 Being born in the month of March. Choosing a blue bead at 6 5 Getting a 5 on the spinner. random from the bag. 4 5 5 5

15/01/2022 Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 EQUALLY LIKELY OUTCOMES

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability as a fraction § For equally likely outcomes § § number of successful outcomes Probability = total number of possible outcomes We use a P then some brackets to shorten what we need to write “The probability of getting a green marble” can be shortened to P(green) 3 green marbles 3 P(green) = 10 out of 10 marbles altogether

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Example – What is the probability of the following events? 1) A coin landing tails up? P(tails) = 2) This spinner stopping on the red section? P(red) = 3) Drawing a seven of hearts from a pack of 52 cards? P(7 of ) = 4) A baby being born on a Friday? P(Friday) =

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Example – What is the probability of the following events? 1) A coin landing tails up? P(tails) = 3) Drawing a seven of hearts from a pack of 52 cards? 1 2 P(7 of ) = 2) This spinner stopping on the red section? P(red) = 1 4 1 52 4) A baby being born on a Friday? P(Friday) = 1 7

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 PROBABILITY OF AN EVENT NOT HAPPENING

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 https: //www. youtube. com/watch? v=y 9 T 5 ol 65 m. SU&feature=emb_logo Probability

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability of an outcome NOT happening § This is 1 – the probability of it happening… P(NOT A) = 1 – P(A) § With fractions: Ø Make sure that the top numbers add together to make the bottom number § With decimals: Ø Make sure that the two decimals add up to 1. So what will make it up to 10 tenths, or 100 hundredths, etc § With percentages: Ø Make sure they add up to 100
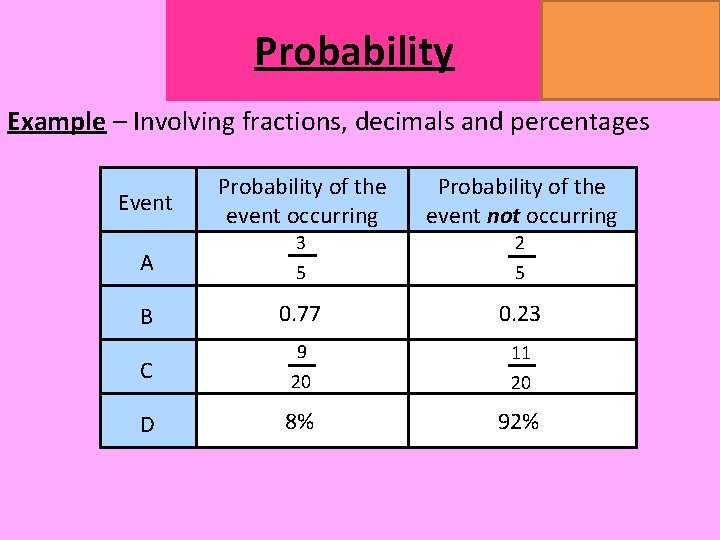
MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Example – Involving fractions, decimals and percentages Event Probability of the event occurring Probability of the event not occurring A 3 5 2 5 B 0. 77 0. 23 9 C 20 11 20 D 8% 92%
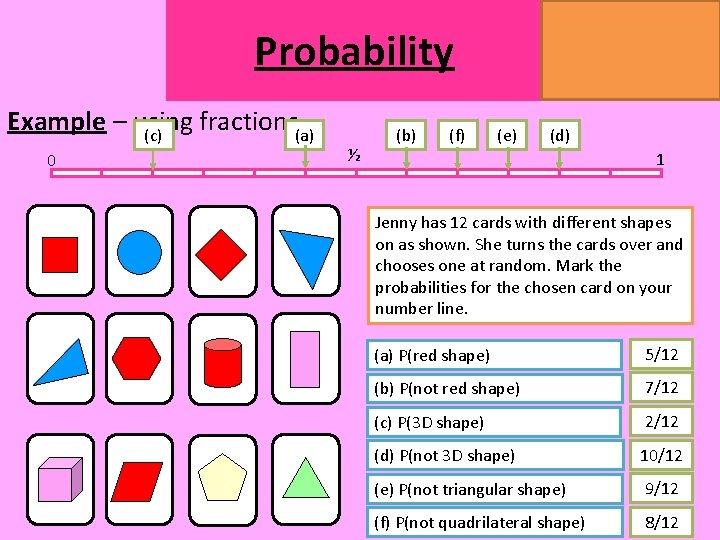
MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Example – using fractions(a) (c) 0 ½ (b) (f) (e) (d) 1 Jenny has 12 cards with different shapes on as shown. She turns the cards over and chooses one at random. Mark the probabilities for the chosen card on your number line. (a) P(red shape) 5/12 (b) P(not red shape) 7/12 (c) P(3 D shape) 2/12 (d) P(not 3 D shape) 10/12 (e) P(not triangular shape) 9/12 (f) P(not quadrilateral shape) 8/12

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Task – now you try these… ½ 0 3 17 24 1 (b) Sam has 6 cards with different numbers on as shown. He turns the cards over and chooses one at random. Mark the probabilities for the chosen card on your number line. (a) P(not even) (b) P(not prime) 15 7 12 (c) P(not a multiple of 3) (d) P(not less than 18) (e) P(not greater than 20) (f) P(not less than 7 factors)
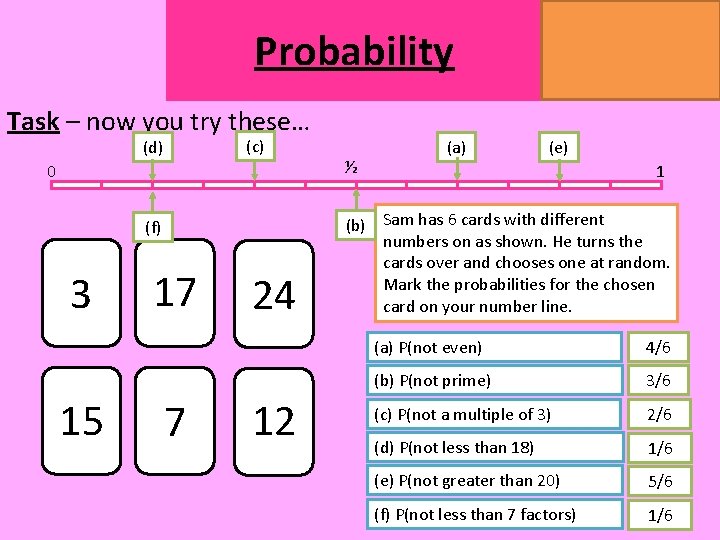
Probability Task – now you try these… (c) (d) 0 (f) 3 15 17 7 24 12 ½ (a) MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 (e) 1 (b) Sam has 6 cards with different numbers on as shown. He turns the cards over and chooses one at random. Mark the probabilities for the chosen card on your number line. (a) P(not even) 4/6 (b) P(not prime) 3/6 (c) P(not a multiple of 3) 2/6 (d) P(not less than 18) 1/6 (e) P(not greater than 20) 5/6 (f) P(not less than 7 factors) 1/6
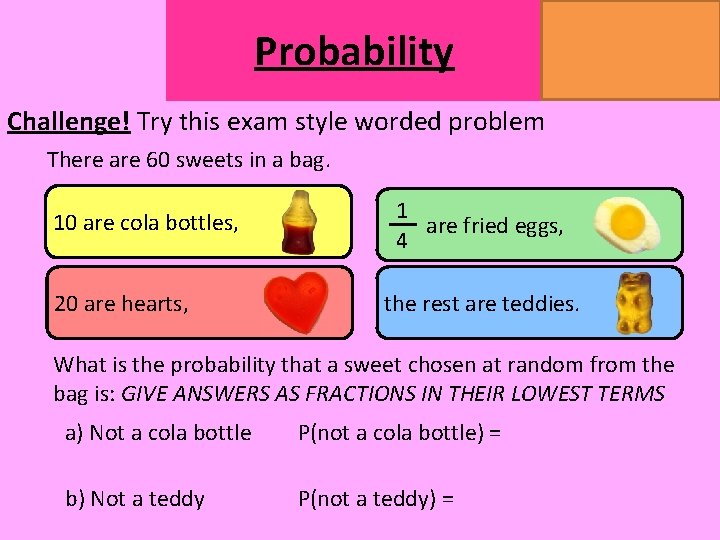
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Challenge! Try this exam style worded problem There are 60 sweets in a bag. 10 are cola bottles, 20 are hearts, 1 are fried eggs, 4 the rest are teddies. What is the probability that a sweet chosen at random from the bag is: GIVE ANSWERS AS FRACTIONS IN THEIR LOWEST TERMS a) Not a cola bottle P(not a cola bottle) = b) Not a teddy P(not a teddy) =
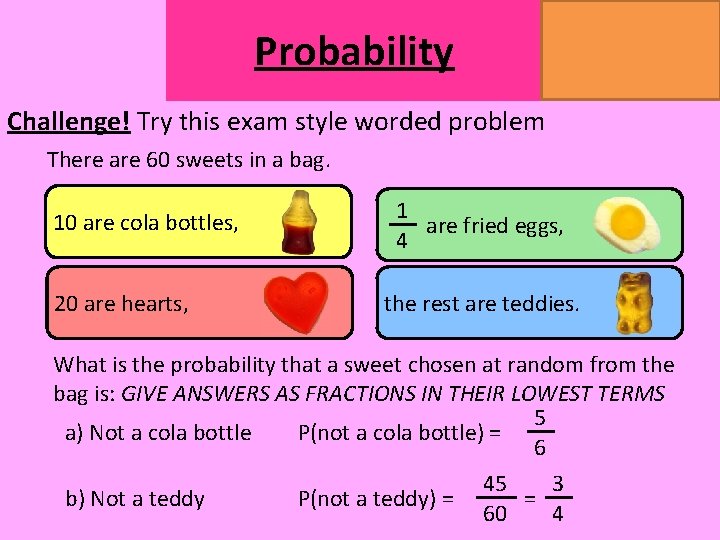
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Challenge! Try this exam style worded problem There are 60 sweets in a bag. 10 are cola bottles, 20 are hearts, 1 are fried eggs, 4 the rest are teddies. What is the probability that a sweet chosen at random from the bag is: GIVE ANSWERS AS FRACTIONS IN THEIR LOWEST TERMS 5 P(not a cola bottle) = a) Not a cola bottle 6 45 3 P(not a teddy) = b) Not a teddy = 60 4

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 RELATIVE FREQUENCY AND ESTIMATION
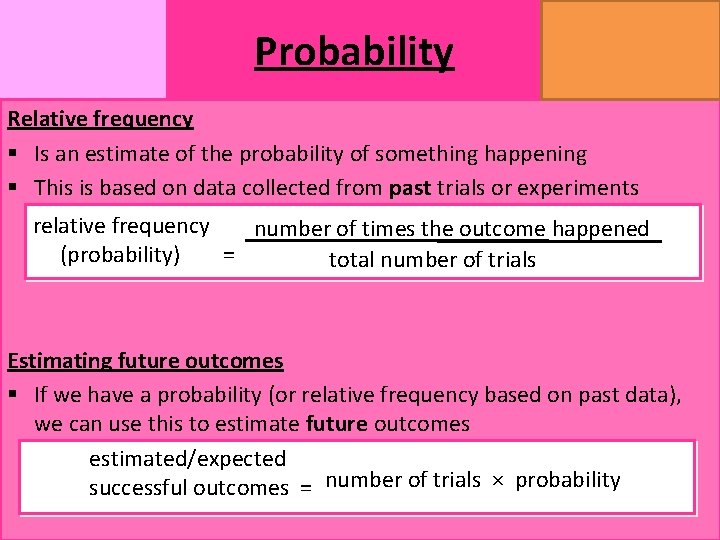
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Relative frequency § Is an estimate of the probability of something happening § This is based on data collected from past trials or experiments relative frequency number of times the outcome happened (probability) = total number of trials Estimating future outcomes § If we have a probability (or relative frequency based on past data), we can use this to estimate future outcomes estimated/expected successful outcomes = number of trials × probability
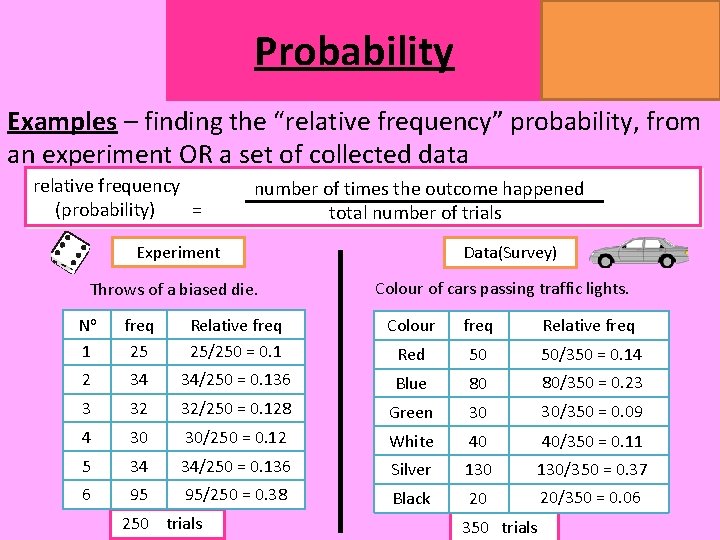
MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Examples – finding the “relative frequency” probability, from an experiment OR a set of collected data relative frequency (probability) = number of times the outcome happened total number of trials Experiment Throws of a biased die. Data(Survey) Colour of cars passing traffic lights. No 1 freq 25 Relative freq 25/250 = 0. 1 Colour freq Relative freq Red 50 50/350 = 0. 14 2 34 34/250 = 0. 136 Blue 80 80/350 = 0. 23 3 32 32/250 = 0. 128 Green 30 30/350 = 0. 09 4 30 30/250 = 0. 12 White 40 40/350 = 0. 11 5 34 34/250 = 0. 136 Silver 130/350 = 0. 37 6 95 95/250 = 0. 38 Black 20 20/350 = 0. 06 250 trials 350 trials
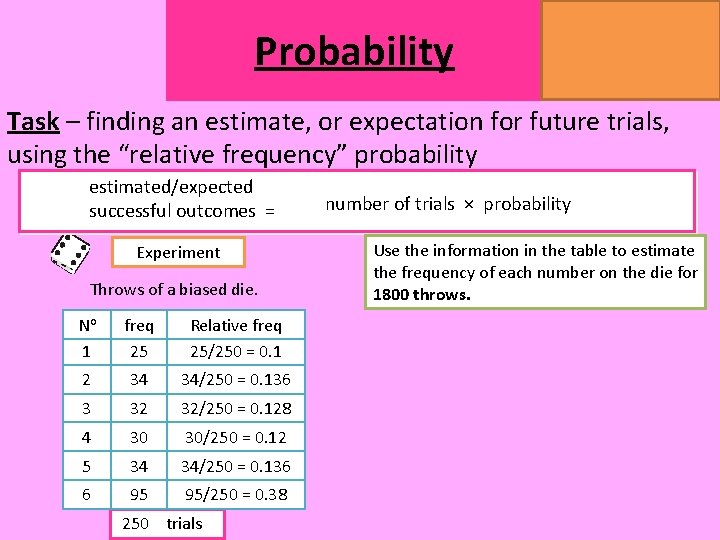
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Task – finding an estimate, or expectation for future trials, using the “relative frequency” probability estimated/expected successful outcomes = Experiment Throws of a biased die. No 1 freq 25 Relative freq 25/250 = 0. 1 2 34 34/250 = 0. 136 3 32 32/250 = 0. 128 4 30 30/250 = 0. 12 5 34 34/250 = 0. 136 6 95 95/250 = 0. 38 250 trials number of trials × probability Use the information in the table to estimate the frequency of each number on the die for 1800 throws.
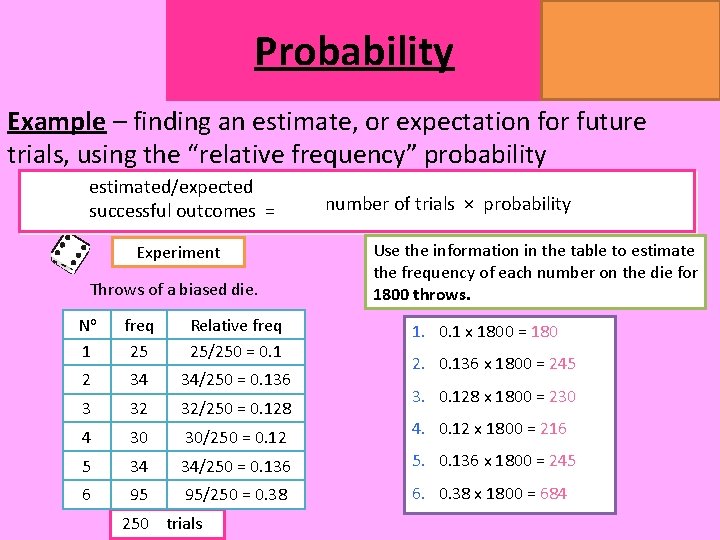
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Example – finding an estimate, or expectation for future trials, using the “relative frequency” probability estimated/expected successful outcomes = Experiment Throws of a biased die. number of trials × probability Use the information in the table to estimate the frequency of each number on the die for 1800 throws. No 1 freq 25 Relative freq 25/250 = 0. 1 2 34 34/250 = 0. 136 3 32 32/250 = 0. 128 4 30 30/250 = 0. 12 4. 0. 12 x 1800 = 216 5 34 34/250 = 0. 136 5. 0. 136 x 1800 = 245 6 95 95/250 = 0. 38 6. 0. 38 x 1800 = 684 250 trials 1. 0. 1 x 1800 = 180 2. 0. 136 x 1800 = 245 3. 0. 128 x 1800 = 230
MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Task – worded question A bag contains an unknown number of coloured discs. Rebecca selects a disc at random from the bag, notes its colour, then replaces it. She does this 500 times and her results are recorded in the table below. Rebecca hands the bag to Peter who is going to select one disc from the bag. Use the information from the table to find estimates for: (a) The probability that Peter selects a red disc. (b) The probability that he selects a blue disc. (c) The number of yellow discs that Rebecca could expect for 1800 trials. Blue Green Red Yellow White 8 85 200 115 92 (a) P(Red) = (b) P(Blue) = (c) Yellow = ?
MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Example – worded question A bag contains an unknown number of coloured discs. Rebecca selects a disc at random from the bag, notes its colour, then replaces it. She does this 500 times and her results are recorded in the table below. Rebecca hands the bag to Peter who is going to select one disc from the bag. Use the information from the table to find estimates for: (a) The probability that Peter selects a red disc. (b) The probability that he selects a blue disc. (c) The number of yellow discs that Rebecca could expect for 1800 trials. Blue Green Red Yellow White 8 85 200 115 92 (a) P(Red) = 200/500 = 2/5 or 0. 4 or 40% (b) P(Blue) = 8/500 = 2/125 or 0. 016 or 1. 6% (c) Yellow = 115/500 = 0. 23. So 0. 23 x 1800 = 414 ?

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Task – using probability to make estimations 1. A coin is biased so that the probability of getting heads is 3/5. Dave is going to throw the coin 120 times. Work out an estimate for the number of times the coin lands on tails. 2. The chance of rain each day in April is 2/3. Estimate the number of days you can expect rain in April. 3. A door-to-door salesman achieves sales with a probability of 3/10. How many doors must he approach in order to expect an average of 15 sales a day?

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Task – using probability to make estimations 1. A coin is biased so that the probability of getting heads is 3/5. Dave is going to throw the coin 120 times. Work out an estimate for the number of times the coin lands on tails. 72 2. The chance of rain each day in April is 2/3. Estimate the number of days you can expect rain in April. 20 3. A door-to-door salesman achieves sales with a probability of 3/10. How many doors must he approach in order to expect an average of 15 sales a day? 50
- Slides: 32