Probability MATHSWATCH CLIP 14 59 60 125 GRADE

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 L. O. To be able to § Find missing probabilities for mutually exclusive events § Use a sample space or probability distribution to make an estimate for a given number of trials Key Words event, outcome, scale, certain, impossible, likely, unlikely, experimental, mutually exclusive, independent

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 MUTUALLY EXCLUSIVE EVENTS

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Mutually Exclusive Outcomes § Cannot happen at the same time § Probabilities of mutually exclusive events can be added to find the probability of one OR the other Ø P(A or B) = P(A) + P(B) § The sum of all mutually exclusive outcomes is 1

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 https: //www. youtube. com/watch? v=achh. Cbz. YMd. Q&feature=emb_logo Probability

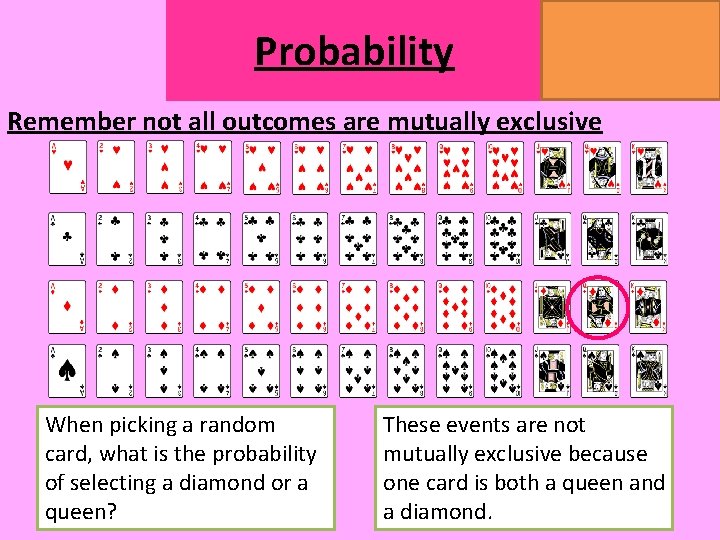
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Remember not all outcomes are mutually exclusive When picking a random card, what is the probability of selecting a diamond or a queen? These events are not mutually exclusive because one card is both a queen and a diamond.

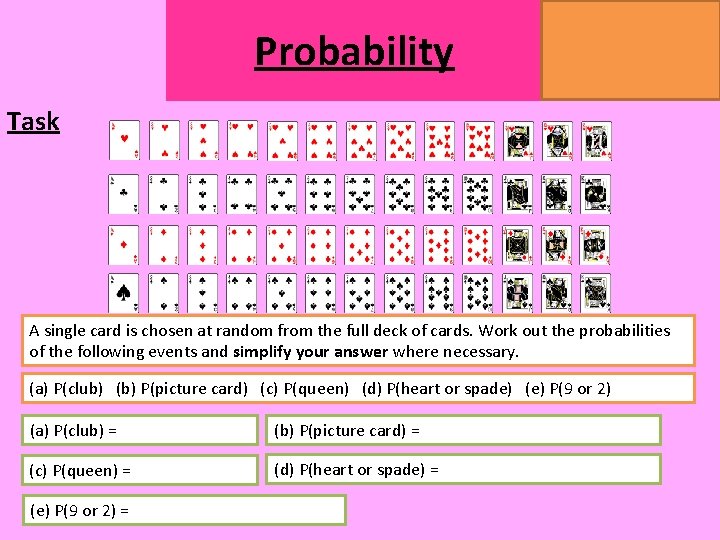
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Task A single card is chosen at random from the full deck of cards. Work out the probabilities of the following events and simplify your answer where necessary. (a) P(club) (b) P(picture card) (c) P(queen) (d) P(heart or spade) (e) P(9 or 2) (a) P(club) = (b) P(picture card) = (c) P(queen) = (d) P(heart or spade) = (e) P(9 or 2) =

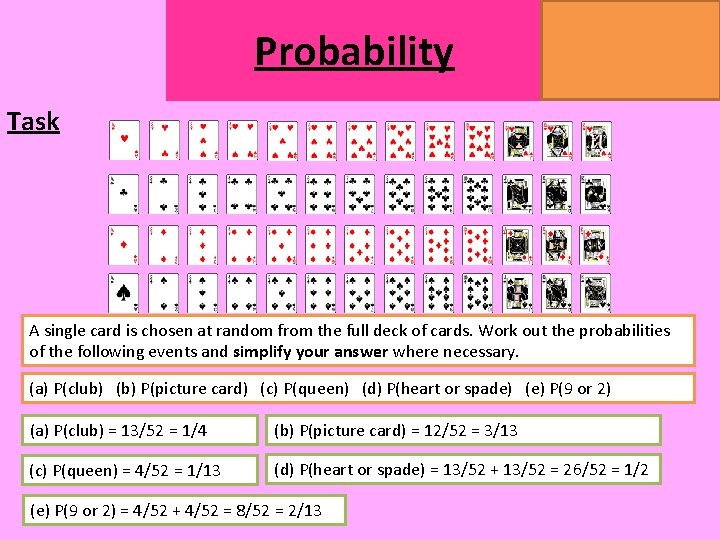
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Task A single card is chosen at random from the full deck of cards. Work out the probabilities of the following events and simplify your answer where necessary. (a) P(club) (b) P(picture card) (c) P(queen) (d) P(heart or spade) (e) P(9 or 2) (a) P(club) = 13/52 = 1/4 (b) P(picture card) = 12/52 = 3/13 (c) P(queen) = 4/52 = 1/13 (d) P(heart or spade) = 13/52 + 13/52 = 26/52 = 1/2 (e) P(9 or 2) = 4/52 + 4/52 = 8/52 = 2/13

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Exam style question A biased 4 -sided spinner has the following probabilities for each section Find the missing probabilities Number 1 2 3 4 Probability 0. 2 x 0. 3 x

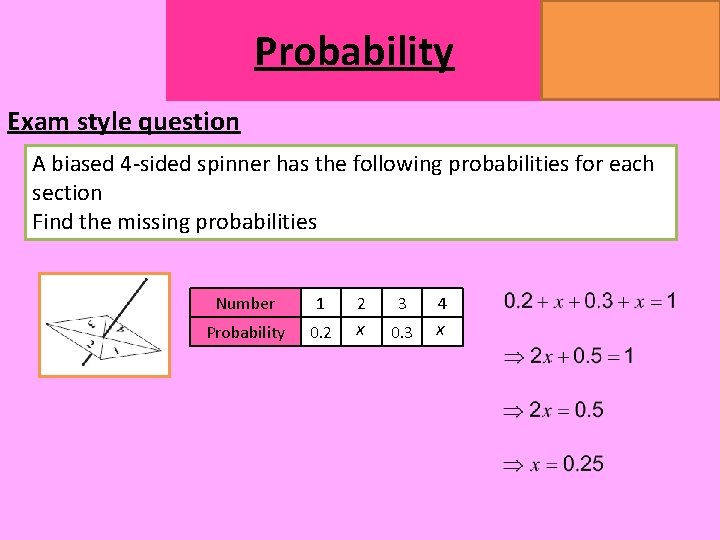
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Exam style question A biased 4 -sided spinner has the following probabilities for each section Find the missing probabilities Number 1 2 3 4 Probability 0. 2 x 0. 3 x

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 INDEPENDENT EVENTS

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Independent events § When the first event has no impact on the probability of the next § Probabilities of independent events can be multiplied to find the probability of one AND the other both happening Ø P(A and B) = P(A) × P(B)

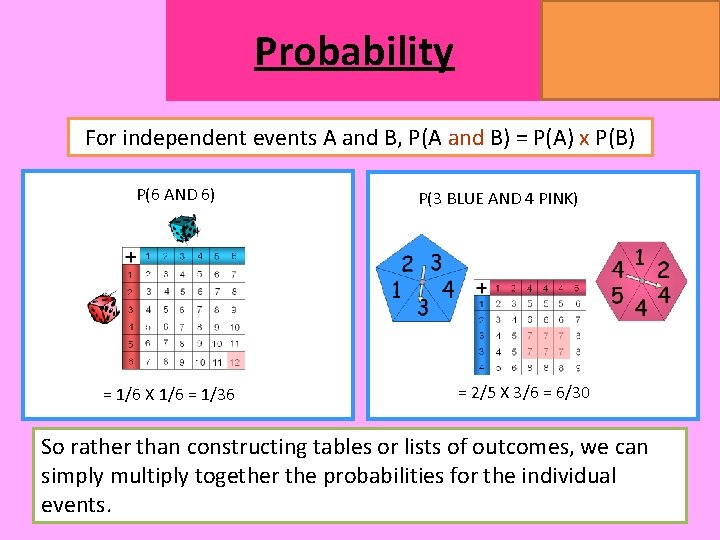
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 For independent events A and B, P(A and B) = P(A) x P(B) P(6 AND 6) = 1/6 X 1/6 = 1/36 P(3 BLUE AND 4 PINK) = 2/5 X 3/6 = 6/30 So rather than constructing tables or lists of outcomes, we can simply multiply together the probabilities for the individual events.

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Both players lay a card at random from their hands as shown. Question 1. What is the probability that two kings are laid? Player 1 P(king and king) = Player 2

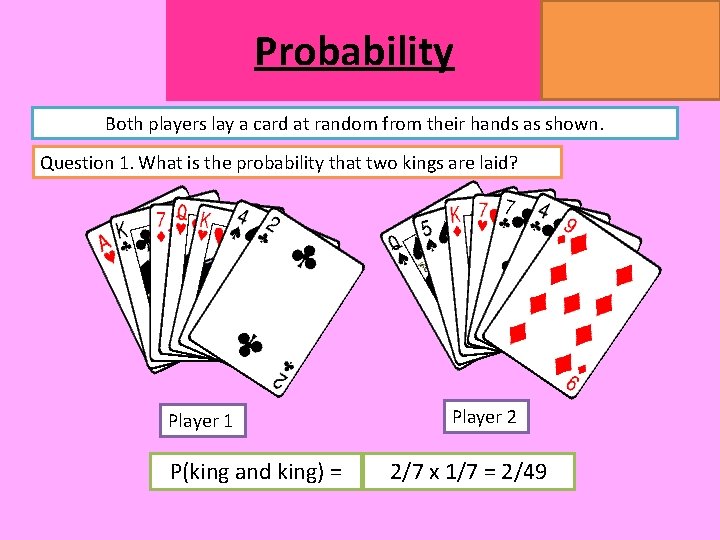
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Both players lay a card at random from their hands as shown. Question 1. What is the probability that two kings are laid? Player 1 P(king and king) = Player 2 2/7 x 1/7 = 2/49

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Both players lay a card at random from their hands as shown. Question 2. What is the probability that two hearts are laid? Player 1 P(heart and heart) = Player 2

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Both players lay a card at random from their hands as shown. Question 2. What is the probability that two hearts are laid? Player 1 P(heart and heart) = Player 2 4/6 x 2/8 = 8/48 (1/6)

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Both players lay a card at random from their hands as shown. Question 3. What is the probability that two picture cards are laid? Player 1 P(picture and picture) = Player 2

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Both players lay a card at random from their hands as shown. Question 3. What is the probability that two picture cards are laid? Player 1 P(picture and picture) = Player 2 2/8 x 5/7 = 10/56 (5/28)

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Both children remove a random bead from their bag Question 4. What are the following probabilities? (a) P(red and red) = (b) P(blue and blue) = (c) P(red and blue) =

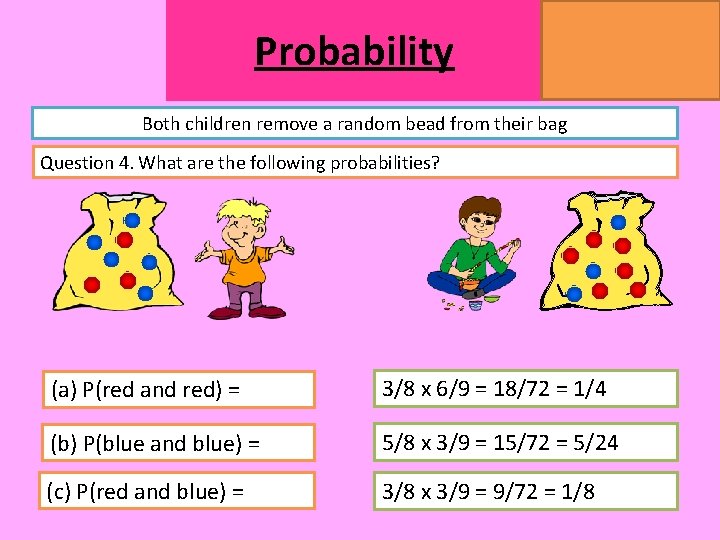
Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Both children remove a random bead from their bag Question 4. What are the following probabilities? (a) P(red and red) = 3/8 x 6/9 = 18/72 = 1/4 (b) P(blue and blue) = 5/8 x 3/9 = 15/72 = 5/24 (c) P(red and blue) = 3/8 x 3/9 = 9/72 = 1/8

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability The pointers on both spinners are spun. Calculate the following probabilities below: 1 2 4 3 2 (a) P(2 and 2) = (b) P(2 and 5) = 2 5 5 4 2 2

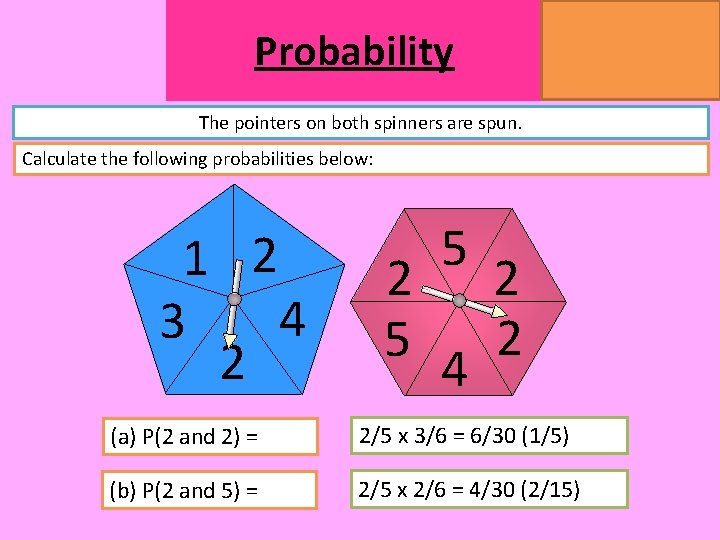
MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability The pointers on both spinners are spun. Calculate the following probabilities below: 1 2 4 3 2 2 5 5 4 2 2 (a) P(2 and 2) = 2/5 x 3/6 = 6/30 (1/5) (b) P(2 and 5) = 2/5 x 2/6 = 4/30 (2/15)

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 The pointers on both spinners are spun. Calculate the following probabilities below: 6 5 4 4 (a) P(4 and 4) = (b) P(5 and 8) = 5 5 3 8 4 4 38

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 The pointers on both spinners are spun. Calculate the following probabilities below: 6 5 4 4 5 5 3 8 4 4 38 (a) P(4 and 4) = 2/6 x 3/8 = 6/48 (1/8) (b) P(5 and 8) = 3/6 x 3/8 = 9/48 (3/16)

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability The pointers on all three spinners are spun. Calculate the following probabilities below: 4 2 4 3 1 (a) P(4 and 5) = (b) P(4 and 6) = (c) P(5 and 6) = 6 5 4 5 5 8 3 5 6 9 4 6 36

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability The pointers on all three spinners are spun. Calculate the following probabilities below: 4 2 4 3 1 6 5 4 5 5 8 3 5 6 9 4 6 36 (a) P(4 and 5) = 2/5 x 3/6 = 6/30 (1/5) (b) P(4 and 6) = 2/5 x 3/8 = 6/40 (3/20) (c) P(5 and 6) = 3/6 x 3/8 = 9/48 (3/16)

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Problem solving with probability! A bag contains some red counters and blue counters. There are n red counters. There is 1 more blue counter than red counters. Bob will take a counter at random from the bag, record the colour and pick another. The probability that Bob picks two red counters is 1/6. Prove that

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Problem solving with probability! A bag contains some red counters and blue counters. There are n red counters. There is 1 more blue counter than red counters. Bob will take a counter at random from the bag, record the colour and pick another. The probability that Bob picks two red counters is 1/6. Prove that red + blue = total P(1 st pick red) = So P(both red) = But P(both red) , giving P(2 nd pick red) =

Probability MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Problem solving with probability! A bag contains some black counters and white counters. There are n black counters. There are 2 less white counters than black counters. Bob will take a counter at random from the bag, record the colour and replaces it before picking another. The probability that Bob picks one of each counter is 3/8. Find how many of each coloured counter there are in the bag

MATHSWATCH CLIP 14, 59, 60, 125 GRADE 1, 2, 3 Probability Problem solving with probability! A bag contains some black counters and white counters. There are n black counters. There are 2 less white counters than black counters. Bob will take a counter at random from the bag, record the colour and replaces it before picking another. The probability that Bob picks one of each counter is 3/8. Find how many of each coloured counter there are in the bag red + blue = total But P(one each) P(BW) = P(WB) = So P(one each) as n > 0 So 3 black, 1 white counter in bag