Probability Lesson 4 4 Conditional Probability and Independence

Probability Lesson 4. 4 Conditional Probability and Independence Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Conditional Probability and Independence Learning Targets After this lesson, you should be able to: ü Find and interpret conditional probabilities using two-way tables. ü Use the conditional probability formula to calculate probabilities. ü Determine whether two events are independent. Statistics and Probability with Applications, 3 rd Edition 2

Independent and Dependent Events Independent events • The occurrence of one of the events does not affect the probability of the occurrence of the other event • Events that are not independent are dependent Statistics and Probability with Applications, 3 rd Edition 3 Larson/Farber 4 th ed 3

Example: Independent and Dependent Events Decide whether the events are independent or dependent. Tossing a coin and getting a head (A), and then rolling a six-sided die and obtaining a 6 (B). Independent (the occurrence of A does not change the probability of the occurrence of B) Larson/Farber 4 th ed Statistics and Probability with Applications, 3 rd Edition 4 4

Example: Independent and Dependent Events Decide whether the events are independent or dependent. Selecting a king from a standard deck (A), not replacing it, and then selecting a queen from the deck (B). Dependent (the occurrence of A changes the probability of the occurrence of B) Larson/Farber 4 th ed Statistics and Probability with Applications, 3 rd Edition 5 5

Conditional Probability and Independence When the probability of an event changes if we know that some other event has occurred, we call this the Conditional Probability of the event. Conditional Probability The probability that one event happens given that another event is known to have happened is called a conditional probability. The conditional probability that event B happens given that event A has happened is denoted by P(B | A). Statistics and Probability with Applications, 3 rd Edition 6

NOTATION ALERT! P(A) means “the probability that event A occurs” P(A B) means “the probability that event A occurs given that B has occurred”. This is conditional probability. Statistics and Probability with Applications, 3 rd Edition 7

We talk about conditional probability when the probability of one event depends on whether or not another event has occurred. e. g. There are 2 red and 3 blue counters in a bag and, without looking, we take out one counter and do not replace it. The probability of a 2 nd counter taken from the bag being red depends on whether the 1 st was red or blue. Conditional probability problems can be solved by considering the individual possibilities or by using a table, a Venn diagram, a tree diagram or a formula. Harder problems are most easily solved by using a formula together with a tree diagram. Statistics and Probability with Applications, 3 rd Edition 8

Probabilities from two way tables American European Asian Total Stu 107 33 55 195 Staff 105 12 47 164 Total 212 45 102 359 What is the probability that the driver is a student? Statistics and Probability with Applications, 3 rd Edition 9

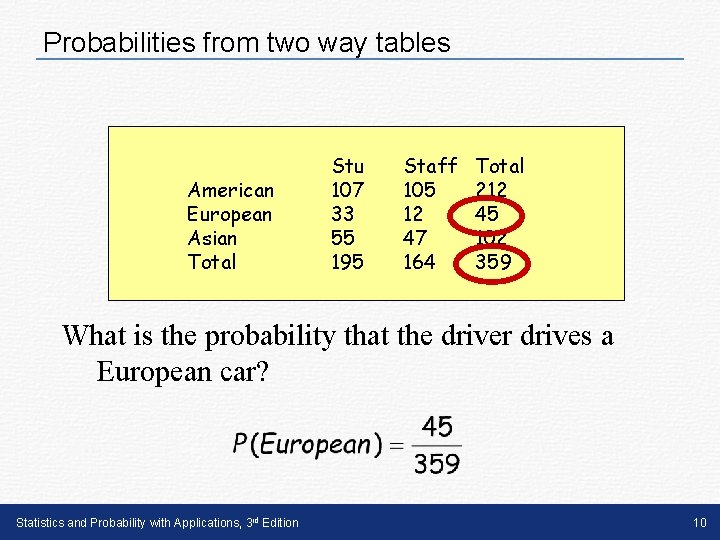
Probabilities from two way tables American European Asian Total Stu 107 33 55 195 Staff 105 12 47 164 Total 212 45 102 359 What is the probability that the driver drives a European car? Statistics and Probability with Applications, 3 rd Edition 10

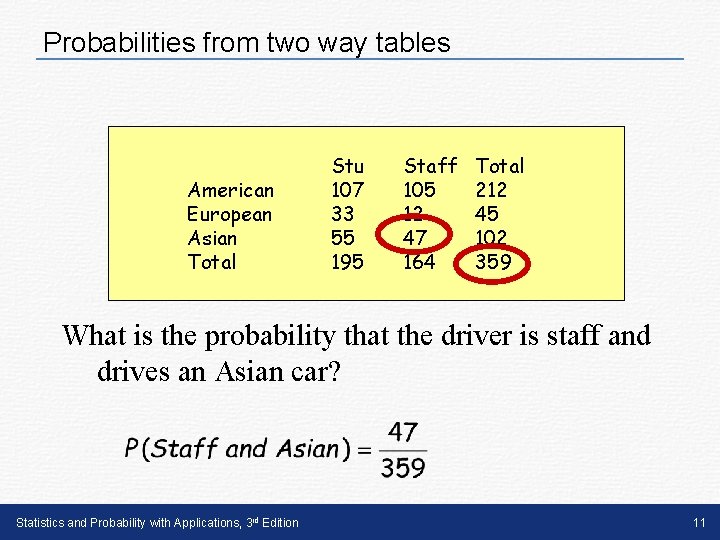
Probabilities from two way tables American European Asian Total Stu 107 33 55 195 Staff 105 12 47 164 Total 212 45 102 359 What is the probability that the driver is staff and drives an Asian car? Statistics and Probability with Applications, 3 rd Edition 11

Probabilities from two way tables Stu 107 33 55 195 American European Asian Total Staff 105 12 47 164 Total 212 45 102 359 If the driver is a student, what is the probability that they drive an American car? Condition Statistics and Probability with Applications, 3 rd Edition 12

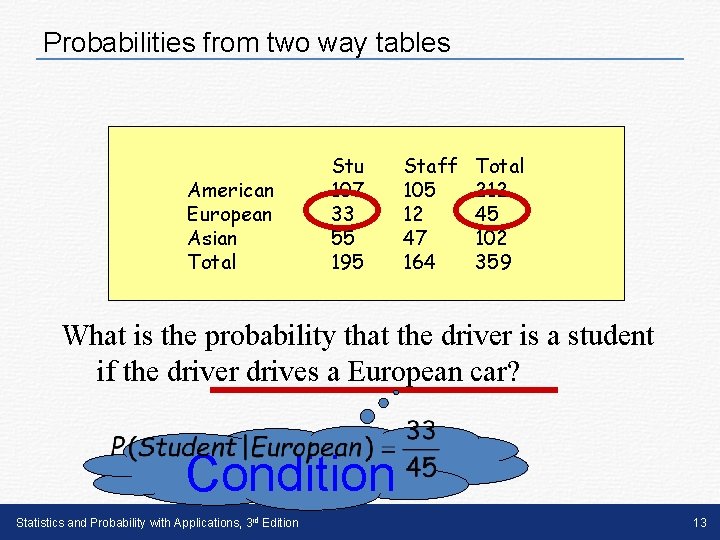
Probabilities from two way tables American European Asian Total Stu 107 33 55 195 Staff 105 12 47 164 Total 212 45 102 359 What is the probability that the driver is a student if the driver drives a European car? Condition Statistics and Probability with Applications, 3 rd Edition 13

Conditional probabilities and two-way tables • Happy, Healthy, Rich, or Famous? One question on the Census at School survey (http: //www. amstat. org/censusatschool/index. cfm) asks students if they would prefer to be happy, healthy, rich or famous. Students may only choose one of these responses. The two-way table below summarizes the responses of 218 high school students from the United States by gender. STATUS GENDER Female Male Total Happy 90 46 136 Healthy 20 13 33 Rich 10 31 41 Famous 0 8 8 Total 120 98 218 Suppose we randomly select one of these 218 students. Define events F: female, H: happy, and R: rich. (a) Find P(H | F). Interpret this value in context. (b) Given that the chosen person did not choose rich, what’s the probability that this person is female? Write your answer as a probability statement using correct symbols for the events. Statistics and Probability with Applications, 3 rd Edition 14

Conditional Probability and Independence By exploring probabilities through a two-way table, we can determine a general formula for computing conditional probabilities. STATUS GENDER Female Male Total Happy 90 46 136 Healthy 20 13 33 Rich 10 31 41 Famous 0 8 8 Total 120 98 218 Calculating Conditional Probabilities To find the conditional probability P(A | B), use the formula Statistics and Probability with Applications, 3 rd Edition 15

In a recent study it was found that the probability that a randomly selected student is a girl is. 51 and is a girl and plays sports is. 10. If the student is female, what is the probability that she plays sports? Statistics and Probability with Applications, 3 rd Edition 16

The probability that a randomly selected student plays sports if they are male is. 31. What is the probability that the student is male and plays sports if the probability that they are male is. 49? Statistics and Probability with Applications, 3 rd Edition 17

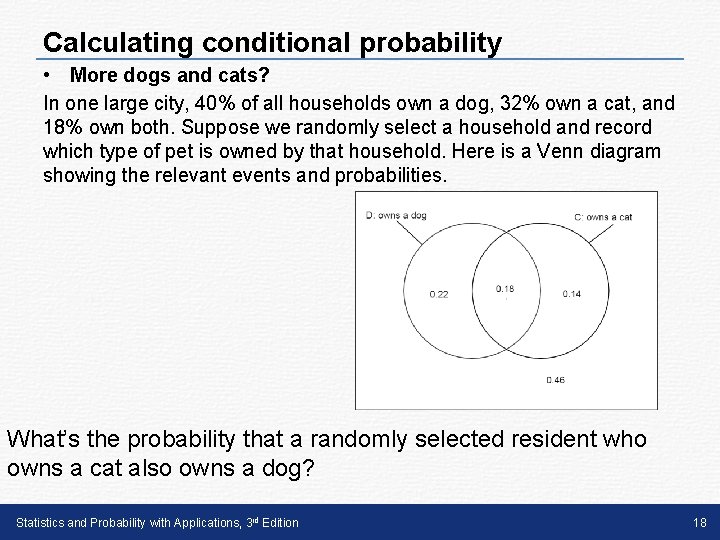
Calculating conditional probability • More dogs and cats? In one large city, 40% of all households own a dog, 32% own a cat, and 18% own both. Suppose we randomly select a household and record which type of pet is owned by that household. Here is a Venn diagram showing the relevant events and probabilities. What’s the probability that a randomly selected resident who owns a cat also owns a dog? Statistics and Probability with Applications, 3 rd Edition 18

Conditional Probability and Independence Suppose you toss a fair coin twice. Define events A: first toss is a head, and B: second toss is a head. We know that P(A) = 1/2 and P(B) = 1/2. • What’s P(B | A)? • It’s the conditional probability that the second toss is a head given that the first toss was a head. • The coin has no memory, so P(B | A) = 1/2. • What’s P(B | AC)? • It’s the conditional probability that the second toss is a head given that the first toss was not a head. Getting a tail on the first toss does not change the probability of getting a head on the second toss, so P(B | AC) = 1/2. In this case, P(B | A) = P(B | AC) = P(B). Knowing whether or not the first toss was a head does not change the probability that the second toss is a head. We say that A and B are independent events. Statistics and Probability with Applications, 3 rd Edition 19

LESSON APP 4. 4 Who earns A’s in college? Students at the University of New Hampshire received 10, 000 course grades in a recent semester. The two-way table breaks down these grades by which school of the university taught the course. School Liberal Arts School Engineering and Physical Sciences School Health and Human Services Grade A 2142 368 882 Grade B 1890 432 630 Grade Lower than B 2268 800 588 The schools are Liberal Arts, Engineering and Physical Sciences (EPS), and Health and Human Services. Choose a University of New Hampshire course grade at random. Consider the two events E: the grade comes from an EPS course, and L: the grade is lower than a B. 1. 2. Find P(L | E). Interpret this probability in context. Are events L and E independent? Justify your answer. Statistics and Probability with Applications, 3 rd Edition 20

Conditional Probability and Independence Learning Targets After this lesson, you should be able to: ü Find and interpret conditional probabilities using two-way tables. ü Use the conditional probability formula to calculate probabilities. ü Determine whether two events are independent. Statistics and Probability with Applications, 3 rd Edition 21