Probability Lesson 4 3 TwoWay Tables and Venn

Probability Lesson 4. 3 Two-Way Tables and Venn Diagrams Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Two-Way Tables and Venn Diagrams Learning Targets After this lesson, you should be able to: ü Use a two-way table to find probabilities. ü Calculate probabilities with the general addition rule. ü Use a Venn diagram to find probabilities. Statistics and Probability with Applications, 3 rd Edition 2

Two-Way Tables and Venn Diagrams Mutually exclusive events A and B cannot both happen at the same time. For such events, “A or B” means that only event A happens or only event B happens. You can find P(A or B) with the addition rule for mutually exclusive events: P(A or B) = P(A) + P(B) How can we find P(A or B) when the two events are not mutually exclusive? Now we have to deal with the fact that “A or B” means one or the other or both. When you’re trying to find probabilities involving two events, like P(A or B), a two-way table can display the sample space in a way that makes probability calculations easier. Statistics and Probability with Applications, 3 rd Edition 3

Two-Way Tables and Venn Diagrams When you’re trying to find probabilities involving two events, like P(A or B), a two-way table can display the sample space in a way that makes probability calculations easier. Consider the example about pierced ears in males and females. Pierced ear Yes Pierced ear No Total Gender Male Gender Female Total 19 84 103 71 4 75 90 88 178 Let event A be the event of being a Male Let event B by the event of having a pierced ear. We want to find P( A or B) however, this event can include A or B or both! Statistics and Probability with Applications, 3 rd Edition 4

Two-Way Tables and Venn Diagrams We can’t use the addition rule for mutually exclusive events unless events A and B have no outcomes in common. In the example, there are 19 outcomes that are shared by events A and B—the students who are male and have a pierced ear. If we did add the probabilities of A and B, we’d get 90/178 + 103/178 = 193/178. This is clearly wrong because the probability is bigger than 1! Statistics and Probability with Applications, 3 rd Edition 5

Two-Way Tables and Venn Diagrams We can fix the double-counting problem illustrated in the two-way table by subtracting the probability P(male and pierced ear), the overlap from the sum. So the P( A or B ) = 90/178 + 103/178 - 19/178 = 174/178 or 87/89 This result is known as the general addition rule. The General Addition Rule for Two Events If A and B are any two events resulting from some chance process, the general addition rule says that P(A or B) = P(A) + P(B) − P(A and B) Statistics and Probability with Applications, 3 rd Edition 6

Example: Using the Addition Rule A blood bank catalogs the types of blood given by donors during the last five days. A donor is selected at random. Find the probability the donor has type O or type A blood. Type O Type A Type B Type AB Total Rh-Positive 156 139 37 12 344 Rh-Negative 28 25 8 4 65 184 164 45 16 409 Total Larson/Farber 4 th ed Statistics and Probability with Applications, 3 rd Edition 7 7

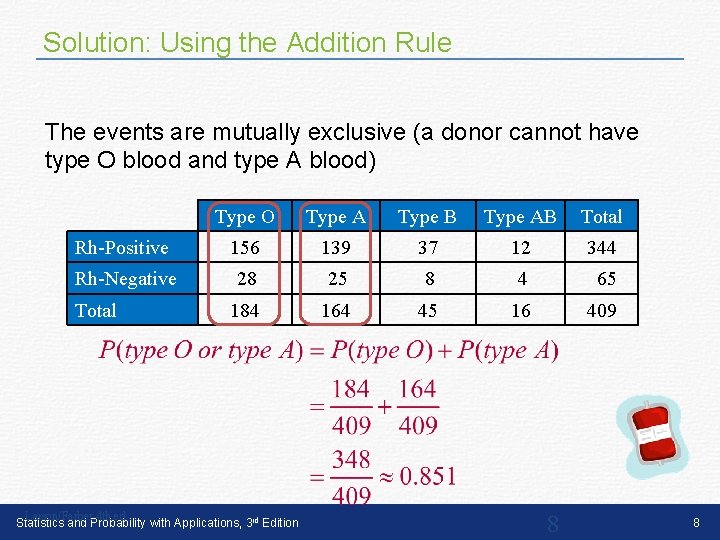
Solution: Using the Addition Rule The events are mutually exclusive (a donor cannot have type O blood and type A blood) Type O Type A Type B Type AB Total Rh-Positive 156 139 37 12 344 Rh-Negative 28 25 8 4 65 184 164 45 16 409 Total Larson/Farber 4 th ed Statistics and Probability with Applications, 3 rd Edition 8 8

Example: Using the Addition Rule Find the probability the donor has type B or is Rh-negative. Type O Type A Type B Type AB Total Rh-Positive 156 139 37 12 344 Rh-Negative 28 25 8 4 65 184 164 45 16 409 Total Solution: The events are not mutually exclusive (a donor can have type B blood and be Rh-negative) Larson/Farber 4 th ed Statistics and Probability with Applications, 3 rd Edition 9 9

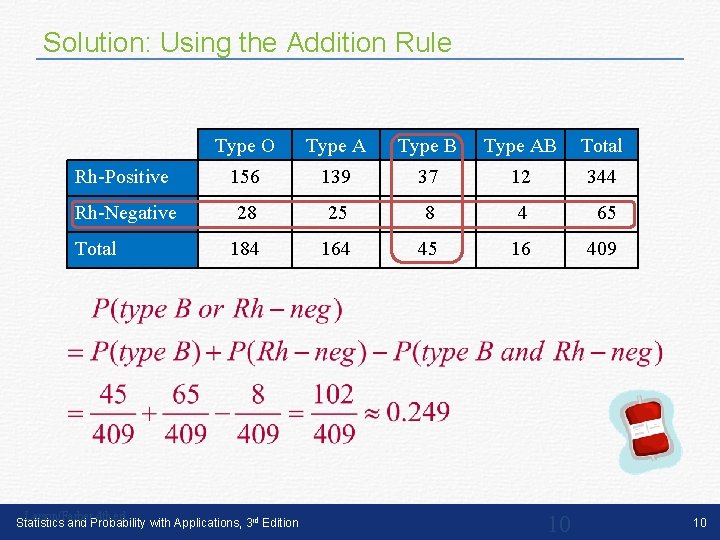
Solution: Using the Addition Rule Type O Type A Type B Type AB Total Rh-Positive 156 139 37 12 344 Rh-Negative 28 25 8 4 65 184 164 45 16 409 Total Larson/Farber 4 th ed Statistics and Probability with Applications, 3 rd Edition 10 10

General Addition Rule • Cell phone or landline? In one large city, 92% of all residents have a cell phone, 64% have a landline, and 59% have both. What’s the probability that a randomly selected resident has a cell phone or a landline? Statistics and Probability with Applications, 3 rd Edition 11

Two-way tables and probability • Happy, Healthy, Rich, or Famous? • One question on the Census at School survey (http: //www. amstat. org/censusatschool/index. cfm) asks students if they would prefer to be happy, healthy, rich or famous. Students may only choose one of these responses. The two-way table below summarizes the responses of 218 high school students from the United States by gender. STATUS Happy Healthy Rich Famous Total GENDER Female 90 20 10 0 120 Male 46 13 31 8 98 Total 136 33 41 8 218 Suppose we choose a student at random from these 218 students. Define event A as getting a female student and event B as getting a student who prefers to be happy. (a) Find P(B). Interpret this value in context. (b) Find P(female and happy). (c) Find P(A or B). Statistics and Probability with Applications, 3 rd Edition 12

Two-Way Tables and Venn Diagrams Two-way tables can be used to illustrate the sample space of a chance process involving two events. So can Venn diagrams. Venn Diagram A Venn diagram consists of one or more circles surrounded by a rectangle. Each circle represents an event. The region inside the rectangle represents the sample space of the chance process. Statistics and Probability with Applications, 3 rd Edition 13

Example: Using the Addition Rule You roll a die. Find the probability of rolling a number less than 3 or rolling an odd number. Solution: The events are not mutually exclusive (1 is an outcome of both events) Roll a Die 4 Odd 3 5 Larson/Farber 4 th ed Statistics and Probability with Applications, 3 rd Edition 6 Less than 1 three 2 14 14

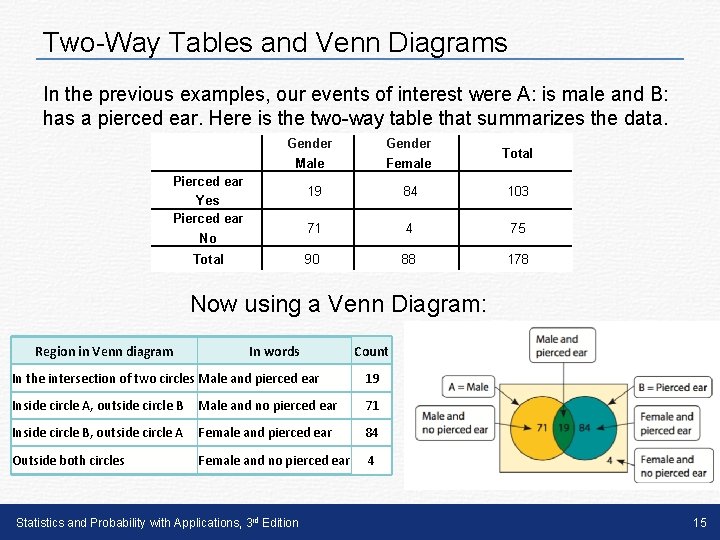
Two-Way Tables and Venn Diagrams In the previous examples, our events of interest were A: is male and B: has a pierced ear. Here is the two-way table that summarizes the data. Gender Male Female Pierced ear Yes Pierced ear No Total 19 84 103 71 4 75 90 88 178 Now using a Venn Diagram: Region in Venn diagram In words Count In the intersection of two circles Male and pierced ear 19 Inside circle A, outside circle B Male and no pierced ear 71 Inside circle B, outside circle A Female and pierced ear 84 Outside both circles Female and no pierced ear 4 Statistics and Probability with Applications, 3 rd Edition 15

Two-Way Tables and Venn Diagrams Some standard vocabulary and notation have been developed to make our work with Venn diagrams a bit easier. • The complement AC contains the outcomes that are not in A. Statistics and Probability with Applications, 3 rd Edition 16

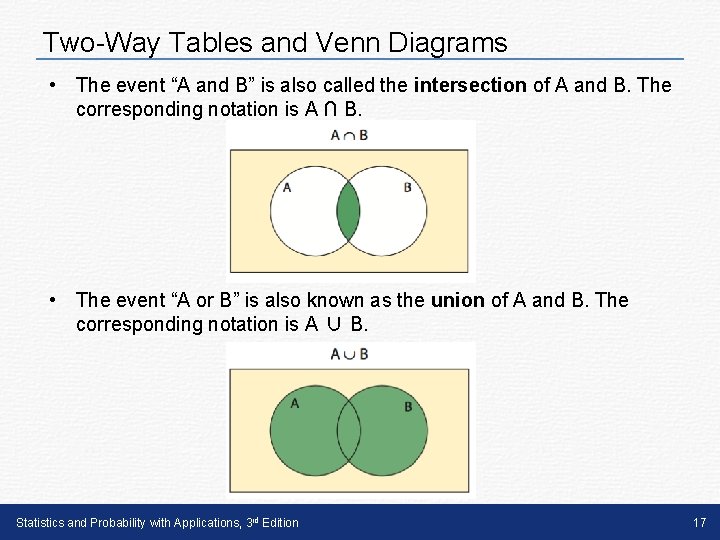
Two-Way Tables and Venn Diagrams • The event “A and B” is also called the intersection of A and B. The corresponding notation is A ∩ B. • The event “A or B” is also known as the union of A and B. The corresponding notation is A ∪ B. Statistics and Probability with Applications, 3 rd Edition 17

Two-Way Tables and Venn Diagrams Intersection, Union • The event “A and B” is called the intersection of events A and B. It consists of all outcomes that are common to both events, and is denoted A ∩ B. • The event “A or B” is called the union of events A and B. It consists of all outcomes that are in event A or event B, or both, and is denoted A ∪ B. With this new notation, we can rewrite the general addition rule in symbols as: P(A ∪ B) = P(A) + P(B) − P(A ∩ B) Statistics and Probability with Applications, 3 rd Edition 18

Venn Diagrams and Probability • Who has pets? In one large city, 40% of all households own a dog, 32% own a cat, and 18% own both. Suppose we randomly select a household and record which type of pet is owned by that household. • (a) Make a Venn diagram to display the sample space of this chance process using the events D: owns a dog and C: owns a cat. • (b) Find the probability that the resident owns a dog and not a cat. Statistics and Probability with Applications, 3 rd Edition 19

LESSON APP 4. 3 Who owns a home? What is the relationship between educational achievement and home ownership? A random sample of 500 U. S. adults was selected. Each member of the sample was identified as a high school graduate (or not) and as a homeowner (or not). The two-way table displays the data. High school graduate Yes High school graduate No Homeowner Yes 221 119 Homeowner No 89 71 Suppose we choose a member of the sample at random. Define events G: is a high school graduate and H: is a homeowner. 1. Explain why P(G or H) ≠ P(G) + P(H). Then find P(G or H). 2. Make a Venn diagram to display the sample space of this chance process. 3. Write the event “is not a high school graduate but is a homeowner” in symbolic form. Statistics and Probability with Applications, 3 rd Edition 20

Two-Way Tables and Venn Diagrams Learning Targets After this lesson, you should be able to: ü Use a two-way table to find probabilities. ü Calculate probabilities with the general addition rule. ü Use a Venn diagram to find probabilities. Statistics and Probability with Applications, 3 rd Edition 21