Probability Independence Sample space Random variable Probability Random

Probability & Independence

• Sample space • Random variable • Probability

Random variable face Y f 1 1/6 2 1/6 3 1/6 4 1/6 5 1/6 6 1/6

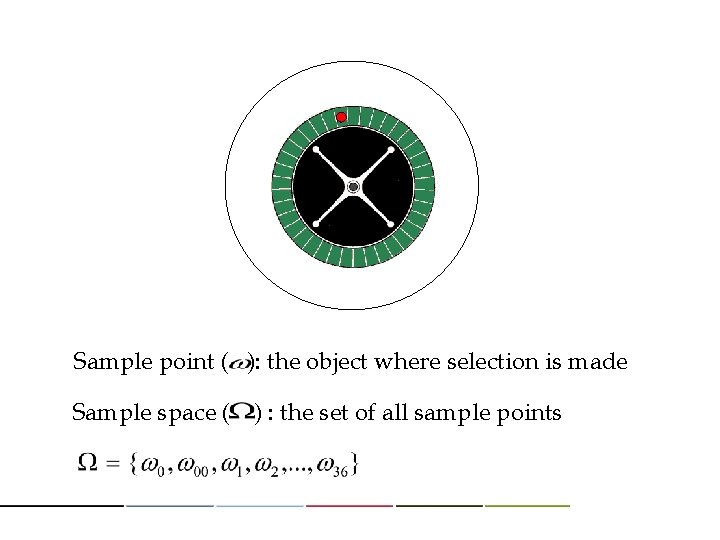
Sample point ( ): the object where selection is made Sample space ( ) : the set of all sample points
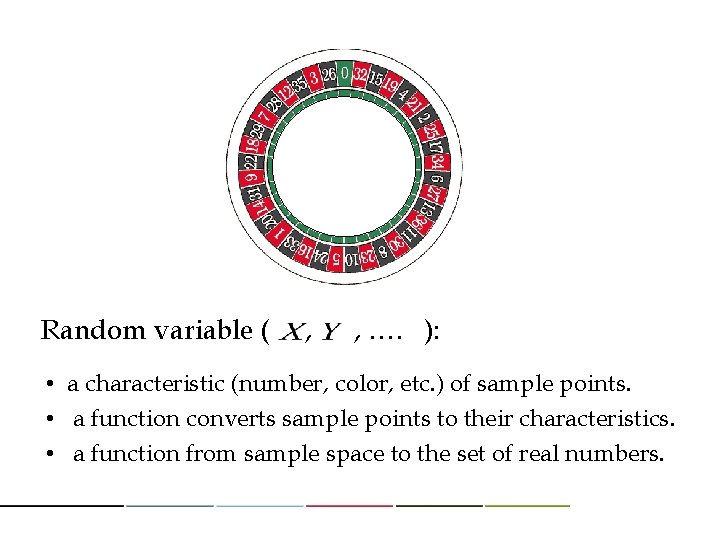
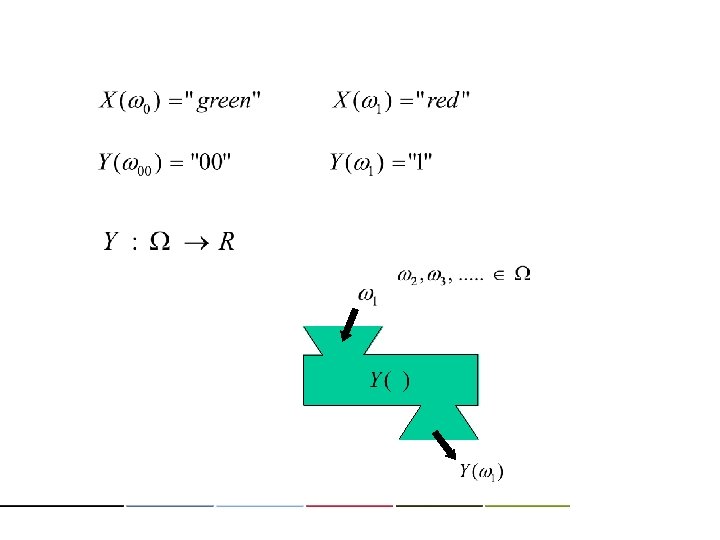
Random variable ( , , …. ): • a characteristic (number, color, etc. ) of sample points. • a function converts sample points to their characteristics. • a function from sample space to the set of real numbers.

Random variables No. Color Even … f 00 Green - 1/38 1 Red X 1/38 2 Black O 1/38 3 Red X 1/38 4 Black O 1/38 35 Black X 1/38 36 Red O 1/38

• Random variable generates subsets of the sample space. • Event: a subset of the sample space
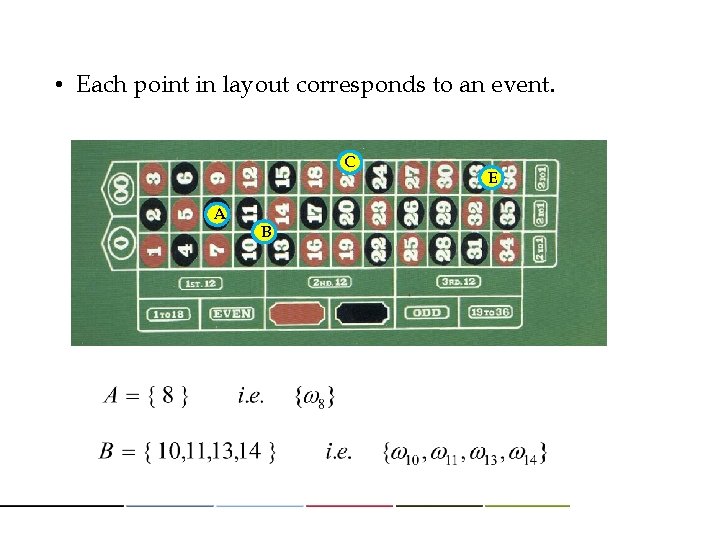
• Each point in layout corresponds to an event. C A B E

• Probability is a function converts events to a number between 0 and 1.

: sample space, the total set, the universal event : complementary event of : null event

: the set of even numbers : multiples of 3 : multiples of 6 : multiples of 2 or 3
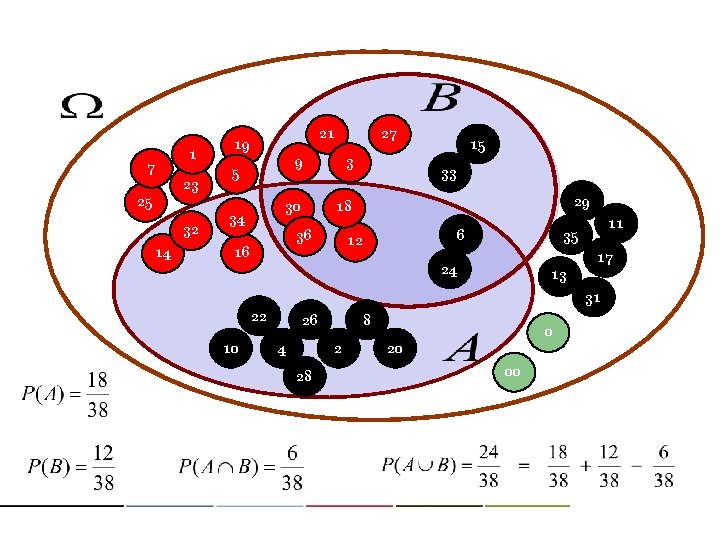
7 1 23 14 9 3 30 18 5 25 32 27 21 19 34 36 33 29 6 12 16 15 11 35 17 24 13 31 22 10 26 4 8 2 28 0 20 00
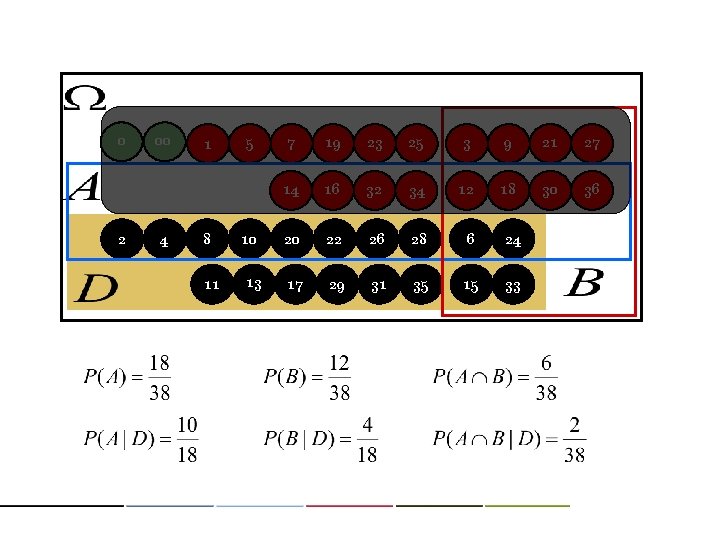
0 2 00 4 1 5 7 19 23 25 3 9 21 27 14 16 32 34 12 18 30 36 8 10 20 22 26 28 6 24 11 13 17 29 31 35 15 33

: sample space, the total set, universal event, roulette, chocolate box, urn : set of subsets of layout
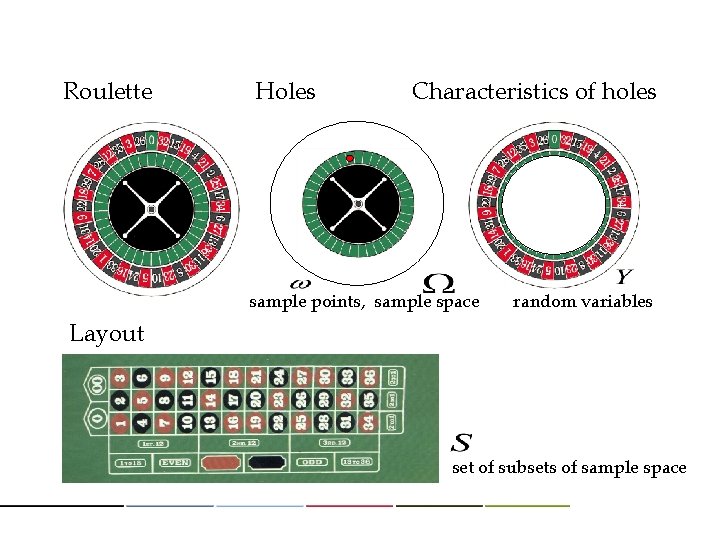
Roulette Holes Characteristics of holes sample points, sample space random variables Layout set of subsets of sample space
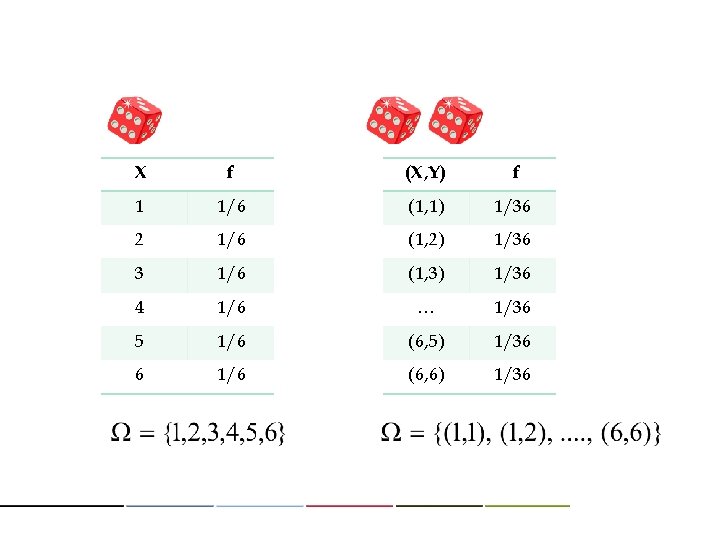
X f (X, Y) f 1 1/6 (1, 1) 1/36 2 1/6 (1, 2) 1/36 3 1/6 (1, 3) 1/36 4 1/6 … 1/36 5 1/6 (6, 5) 1/36 6 1/6 (6, 6) 1/36

How to get money from casino ?


Think coin tossing game. Bet $100 + “all the amount you lose” every time. Then you will win at least a time, then stop there.
$500 House margin Using chips Betting limit



“Who are willing to play a gambling game, seeing rising sun? ”

How to get money from casino ? The best strategy is the one that casinos want to keep out of. That is the strategy leaving casino as soon as possible.

Counterplots of casino: High quality accommodation Far away location

• Joint distribution • Conditional distribution • Independence • Combinatorics
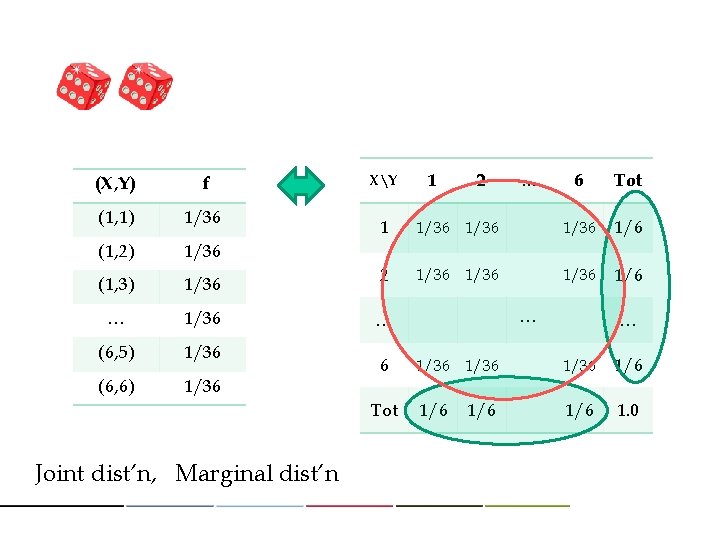
(X, Y) f (1, 1) 1/36 (1, 2) 1/36 (1, 3) 1/36 … 1/36 (6, 5) 1/36 (6, 6) 1/36 XY 2 … 6 Tot 1 1/36 1/6 2 1/36 1/6 … 6 Tot Joint dist’n, Marginal dist’n 1 … … 1/36 1/6 1/6 1. 0 1/6
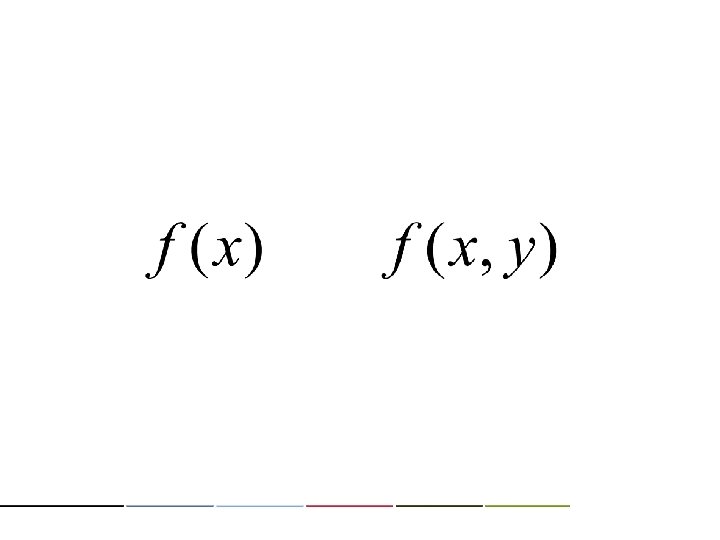
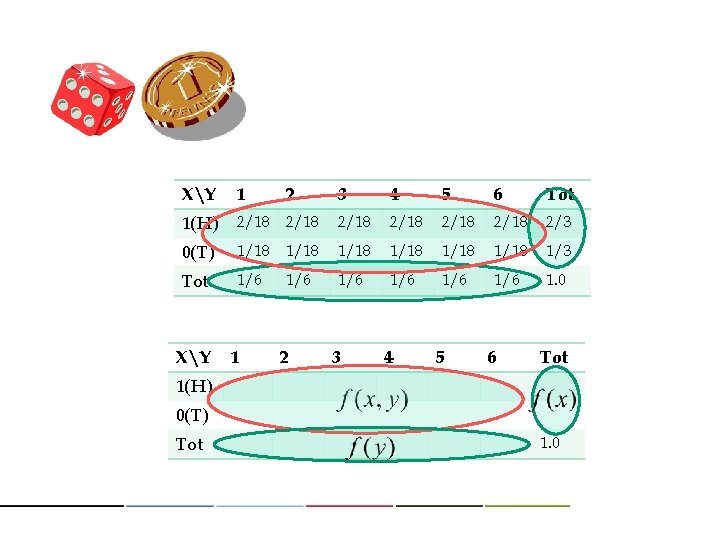
XY 1 1(H) 3 4 5 6 Tot 2/18 2/18 2/3 0(T) 1/18 1/18 1/3 Tot 1/6 1/6 1/6 1. 0 XY 1 2 1/6 2 3 4 5 6 Tot 1(H) 0(T) Tot 1. 0

Independence of random variables XY 1 1(H) 2 3 4 5 6 Tot 2/18 2/18 2/3 0(T) 1/18 1/18 1/3 Tot 1/6 1/6 1/6 1. 0 XY 1 2 3 4 5 6 Tot 1(H) 2/18 1/18 2/18 1/2 0(T) 1/18 2/18 1/2 Tot 1/6 1/6 1/6 1. 0 1/6
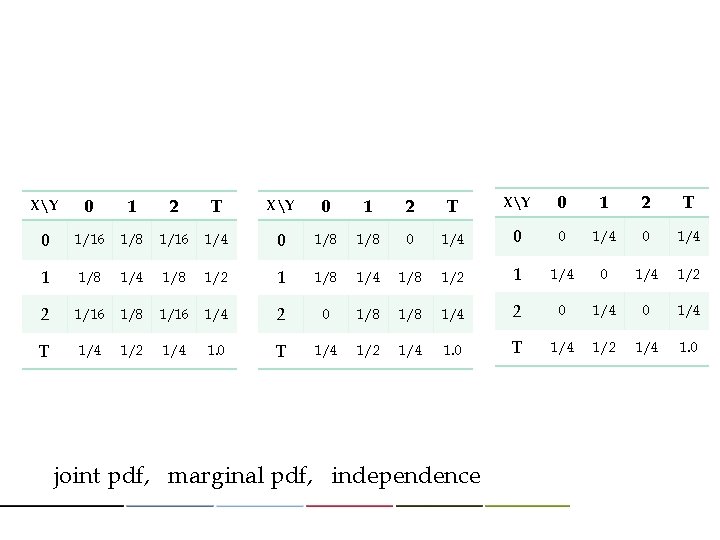
XY 0 1 2 T 0 1/16 1/8 1/16 1/4 0 1/8 0 1/4 1 1/8 1/4 1/8 1/2 1 1/4 0 1/4 1/2 2 1/16 1/8 1/16 1/4 2 0 1/8 1/4 2 0 1/4 T 1/4 1/2 1/4 1. 0 joint pdf, marginal pdf, independence
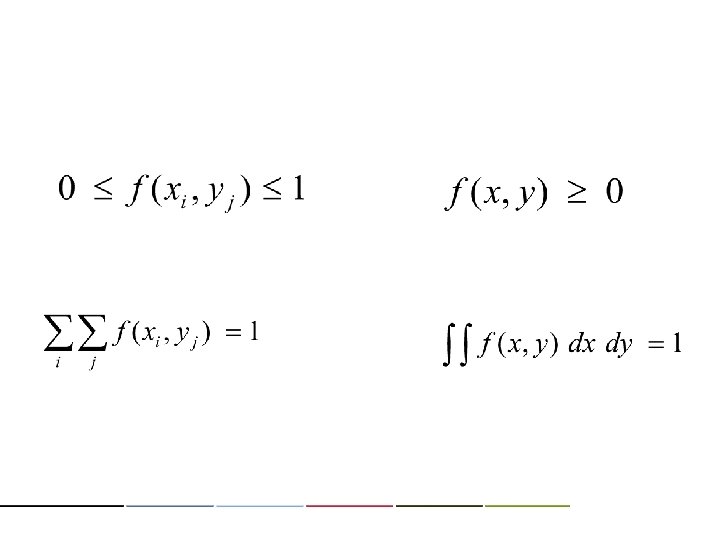
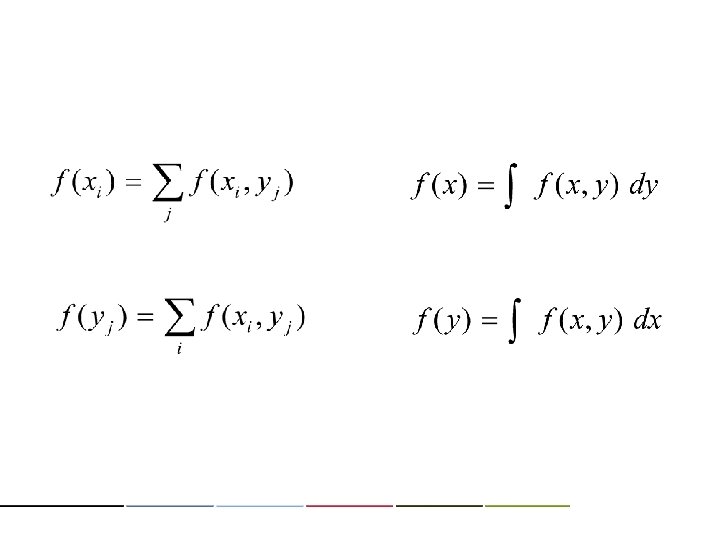
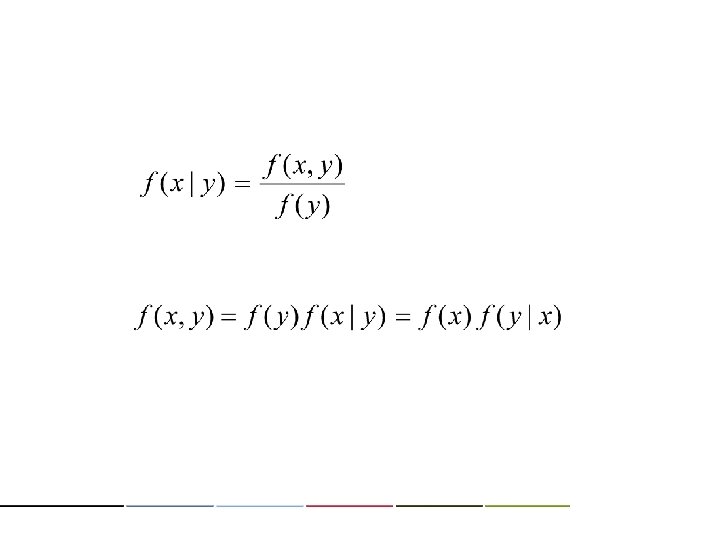
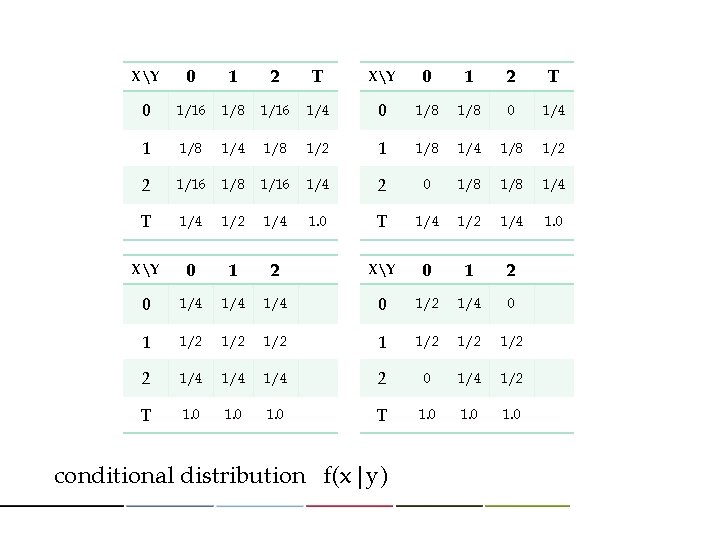
XY 0 1 2 T 0 1/16 1/8 1/16 1/4 0 1/8 0 1/4 1 1/8 1/4 1/8 1/2 2 1/16 1/8 1/16 1/4 2 0 1/8 1/4 T 1/4 1/2 1/4 1. 0 XY 0 1 2 0 1/4 1/4 0 1/2 1/4 0 1 1/2 1/2 1/2 2 1/4 1/4 2 0 1/4 1/2 T 1. 0 1. 0 conditional distribution f(x|y)

XY 0 1 2 T 0 1/4 1/4 0 1/16 1/8 1/16 1/4 0 1/4 1/2 1/4 1. 0 1 1/2 1/2 1 1/8 1/4 1/8 1/2 1 1/4 1/2 1/4 1. 0 2 1/4 1/4 2 1/16 1/8 1/16 1/4 2 1/4 1/2 1/4 1. 0 T 1/4 1/2 1/4 1. 0
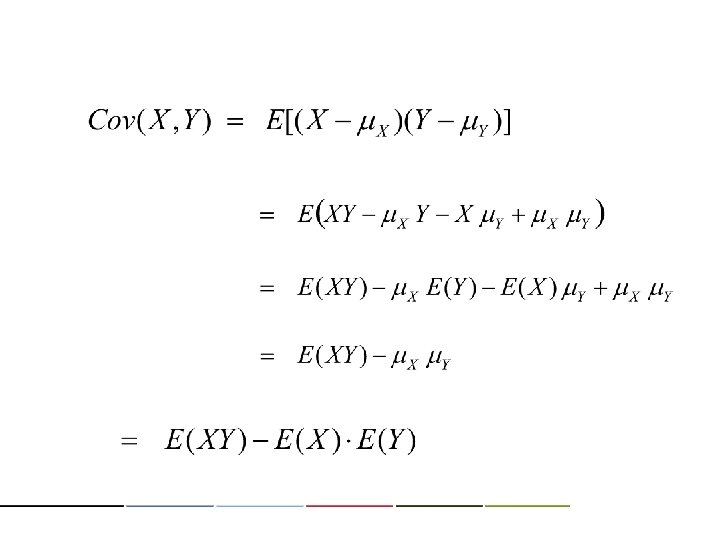
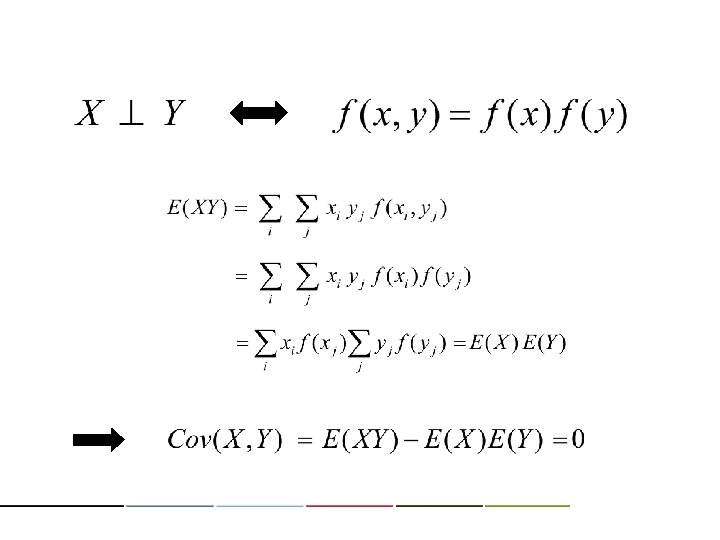

XY 0 1 2 T 0 1/16 1/8 1/16 1/4 0 1/8 0 1/4 1 1/8 1/4 1/8 1/2 1 1/4 0 1/4 1/2 2 1/16 1/8 1/16 1/4 2 0 1/8 1/4 2 0 1/4 T 1/4 1/2 1/4 1. 0
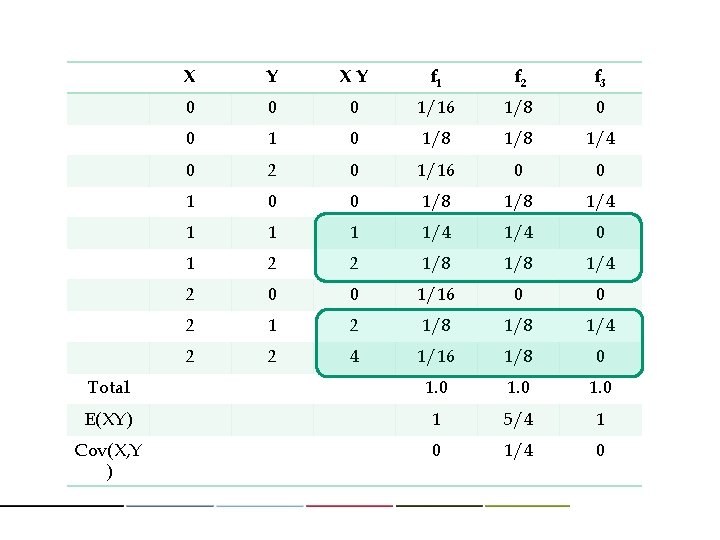
X Y XY f 1 f 2 f 3 0 0 0 1/16 1/8 0 0 1/8 1/4 0 2 0 1/16 0 0 1/8 1/4 1/4 0 1 2 2 1/8 1/4 2 0 0 1/16 0 0 2 1/8 1/4 2 2 4 1/16 1/8 0 Total 1. 0 E(XY) 1 5/4 1 Cov(X, Y ) 0 1/4 0
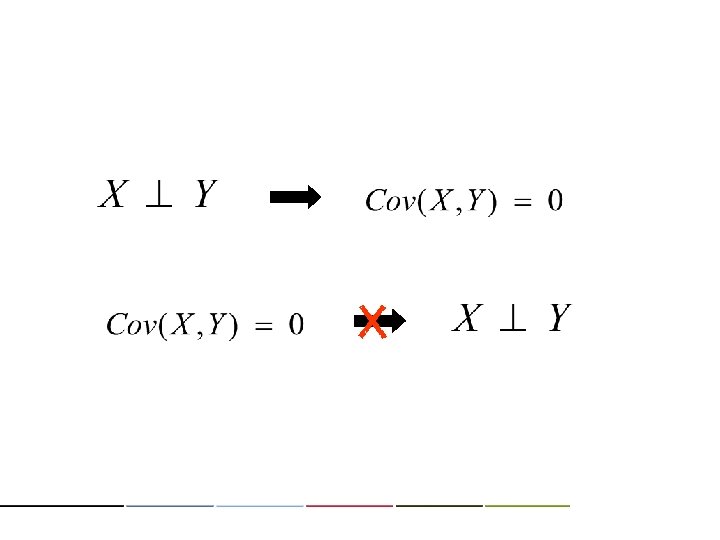
X
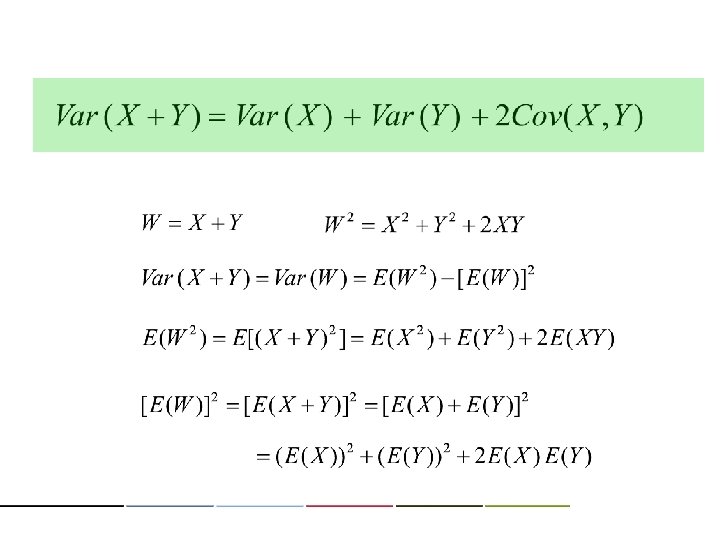
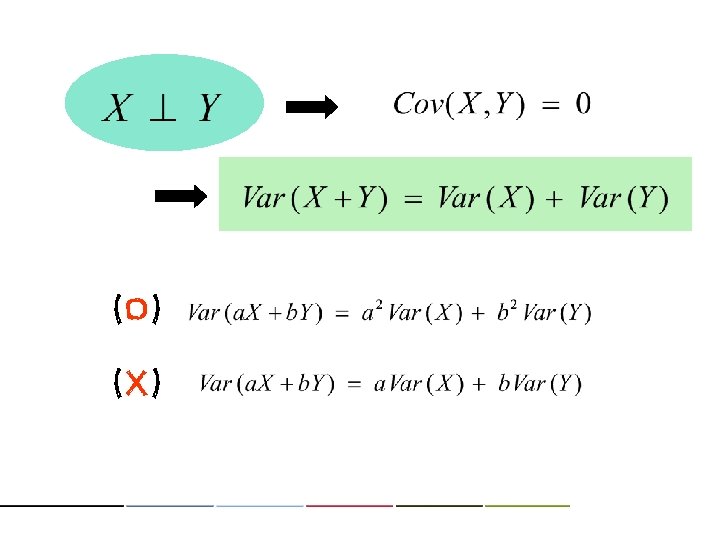
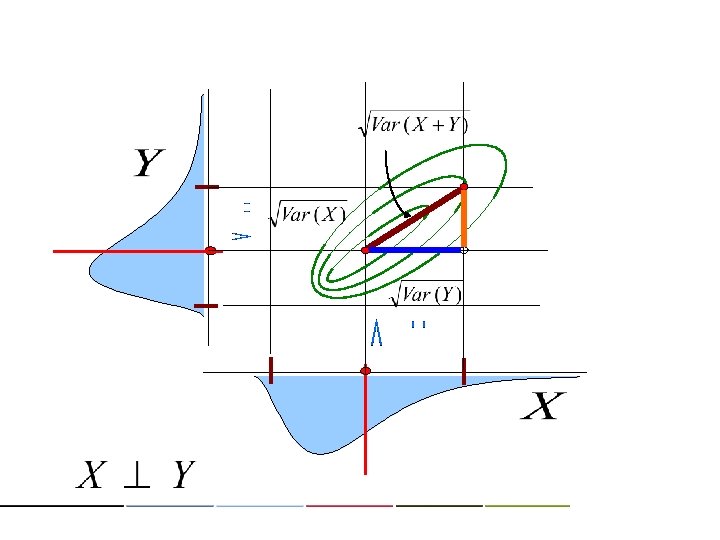

(X) (o) regardless of independence
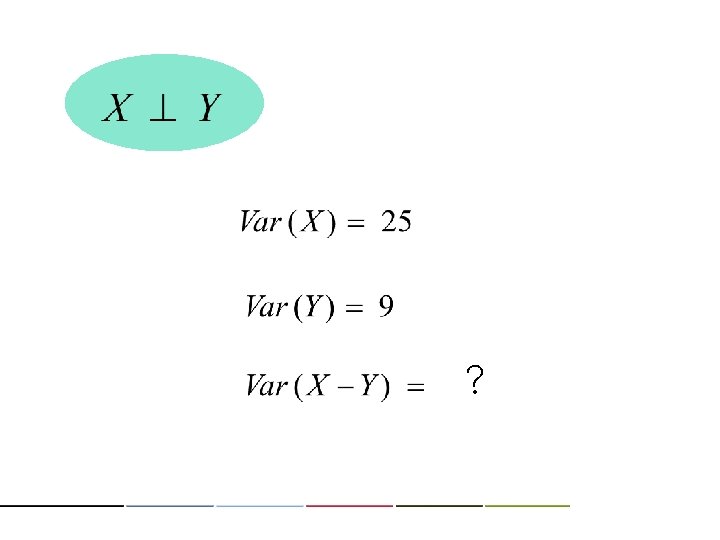
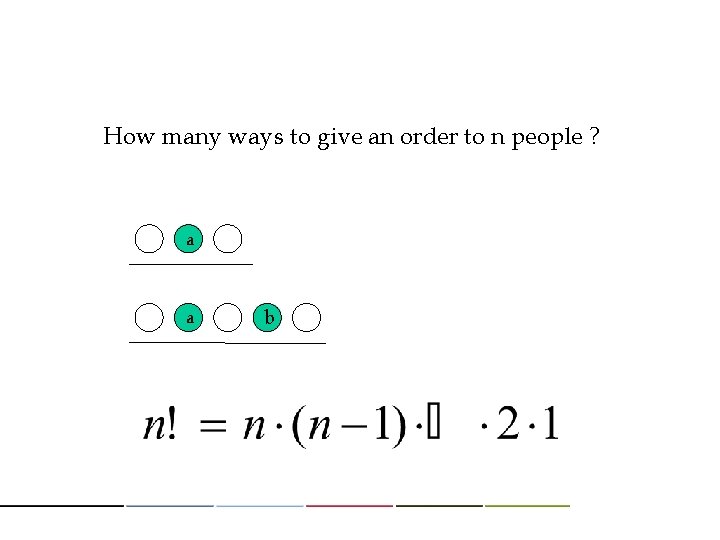
How many ways to give an order to n people ? a a b
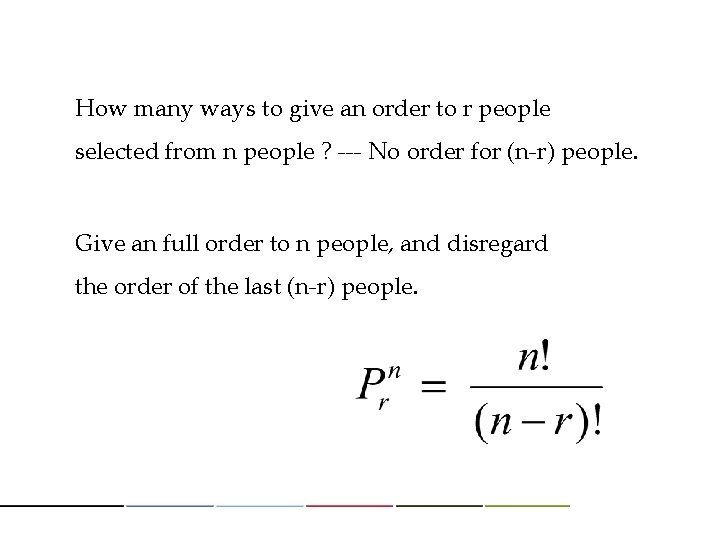
How many ways to give an order to r people selected from n people ? --- No order for (n-r) people. Give an full order to n people, and disregard the order of the last (n-r) people.
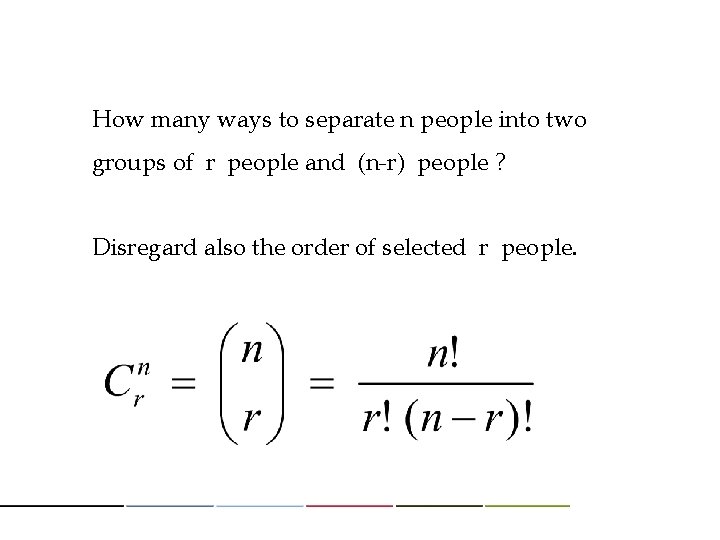
How many ways to separate n people into two groups of r people and (n-r) people ? Disregard also the order of selected r people.

X: the number of heads when we toss a fair coin twice X f 0 0. 25 1 0. 5 2 0. 25 Total 1. 0

Thank you !!
- Slides: 53