Probability Distributions Essential Question What is a probability

Probability Distributions

Essential Question: What is a probability distribution and how is it displayed?

Random Variable • Variable whose value is determined by the outcome of a probability experiment. • Example: roll a die, the variable is the number you roll, possibilities include: numbers 1 -6.

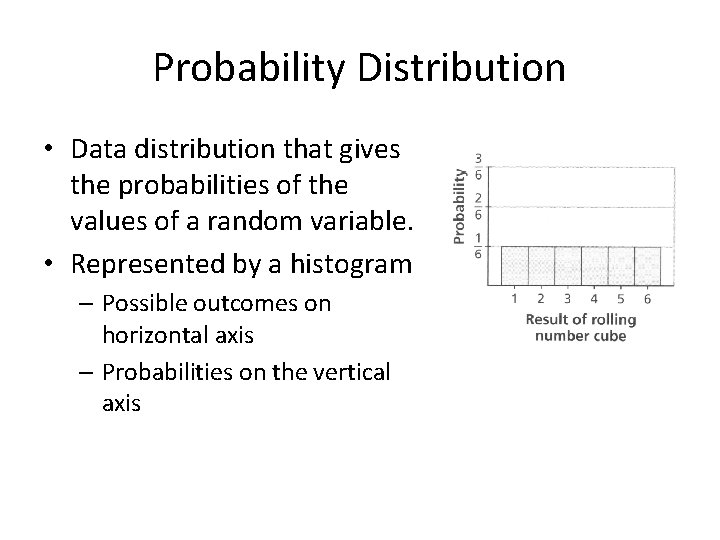
Probability Distribution • Data distribution that gives the probabilities of the values of a random variable. • Represented by a histogram – Possible outcomes on horizontal axis – Probabilities on the vertical axis

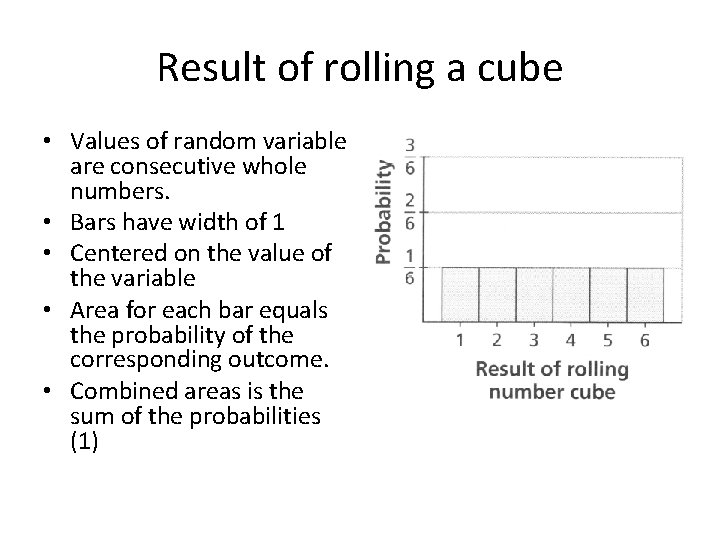
Result of rolling a cube • Values of random variable are consecutive whole numbers. • Bars have width of 1 • Centered on the value of the variable • Area for each bar equals the probability of the corresponding outcome. • Combined areas is the sum of the probabilities (1)

Cumulative Probability • Probability that a random variable is less than or equal to a given value. • Can be found by adding all the areas of the bars for all outcomes less than or equal to the given value.

Reflect 1 a. • In an experiment in which a coin is tossed twice, the random variable X is the number of times that the coins lands heads up. • What are the possible values of the random variable?

Reflect 1 b. • A spinner has 8 equal sections, each labeled 1, 2, 3, or 4. The histogram shows the probability distribution for spinning the spinner. • How many sections of the spinner are labeled with each number? How do you know?

Displaying a Probability Distribution You roll two number cubes at the same time. Let X be a random variable that represents the sum of the numbers you rolled. Make a histogram to show the probability distribution for X.

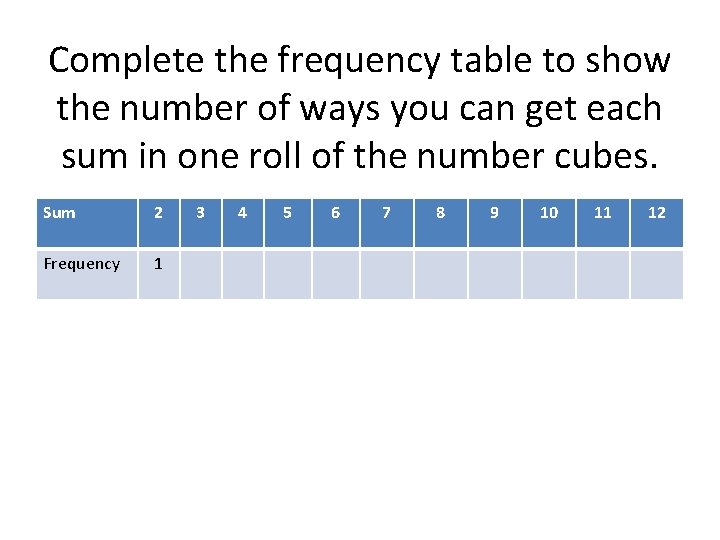
Complete the frequency table to show the number of ways you can get each sum in one roll of the number cubes. Sum 2 Frequency 1 3 4 5 6 7 8 9 10 11 12

Find the total number of outcomes • Add the frequencies you found in part A to find the total number of possible outcomes. • The total number of possible outcomes is: ___

Divide each frequency by the total number of outcomes Sum Probability 2 3 4 5 6 7 8 9 10 11 12

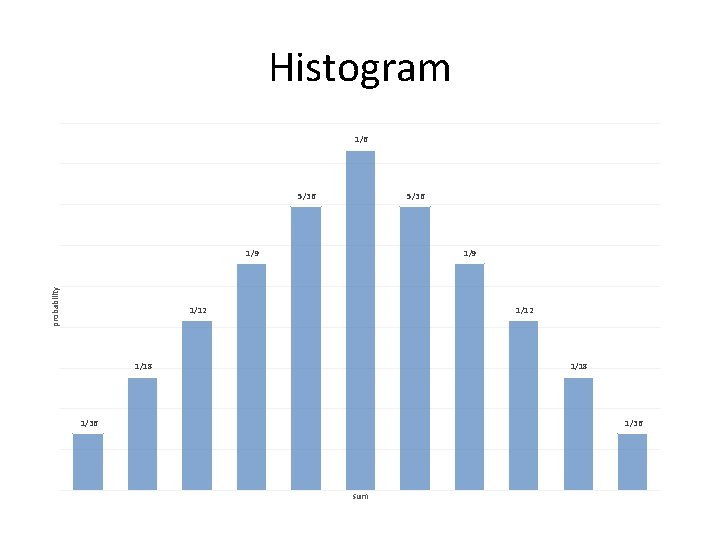
Histogram 1/6 5/36 probability 1/9 1/12 1/18 1/36 sum

Reflect 2 a. •

Theoretical vs. Experimental • Theoretical Probability – finding the probability of events that come from a sample space of known equally likely outcomes. • Experimental Probability – probability of an even occurring when an experiment is conducted.

Using a Simulation • You flip a coin 7 times in a row. • Use a simulation to determine the probability distribution for the number of times the coin lands heads up.

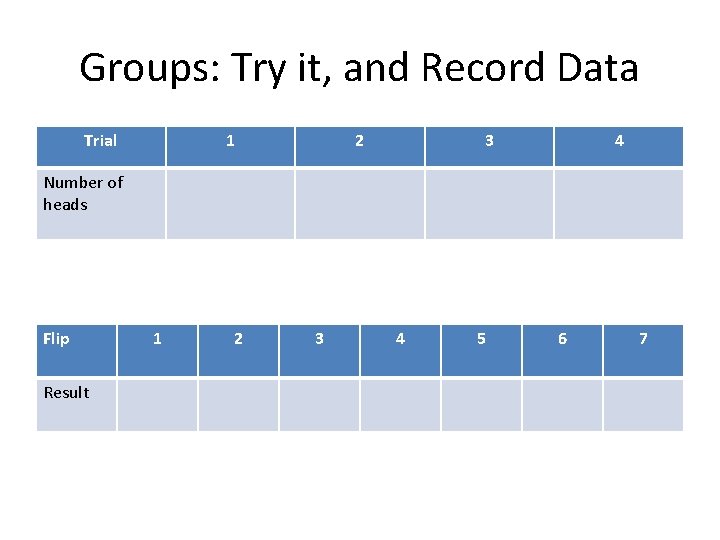
Groups: Try it, and Record Data Trial 1 2 3 4 Number of heads Flip Result 1 2 3 4 5 6 7

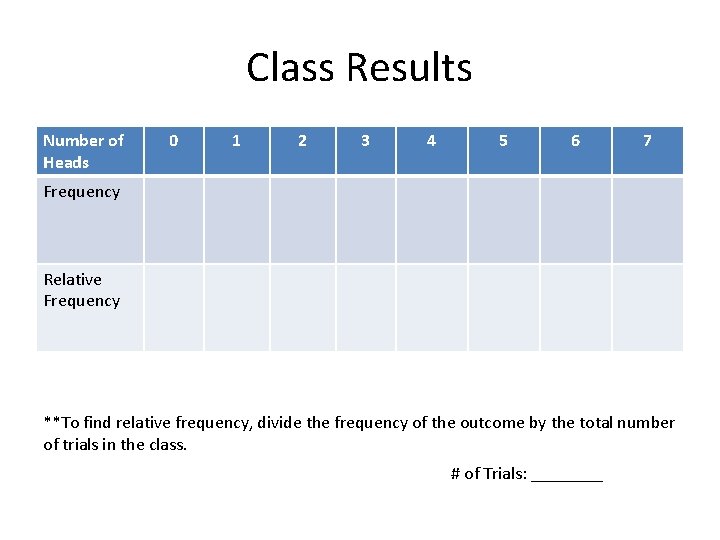
Class Results Number of Heads 0 1 2 3 4 5 6 7 Frequency Relative Frequency **To find relative frequency, divide the frequency of the outcome by the total number of trials in the class. # of Trials: ____

Histogram

Reflect 3 a. • Describe the shape of the probability distribution.

Reflect 3 b. •

Reflect 3 c. • If you flipped a coin 7 times and got 7 heads, would this cause you to question whether the coin is fair? Why or why not?

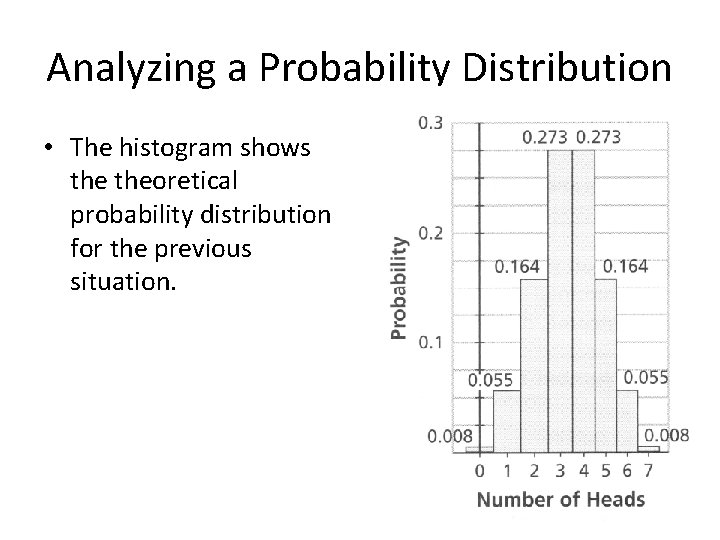
Analyzing a Probability Distribution • The histogram shows theoretical probability distribution for the previous situation.

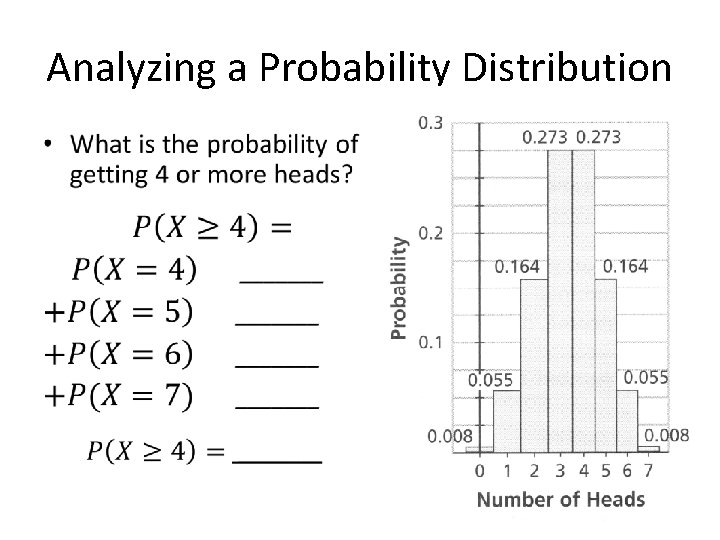
Analyzing a Probability Distribution •

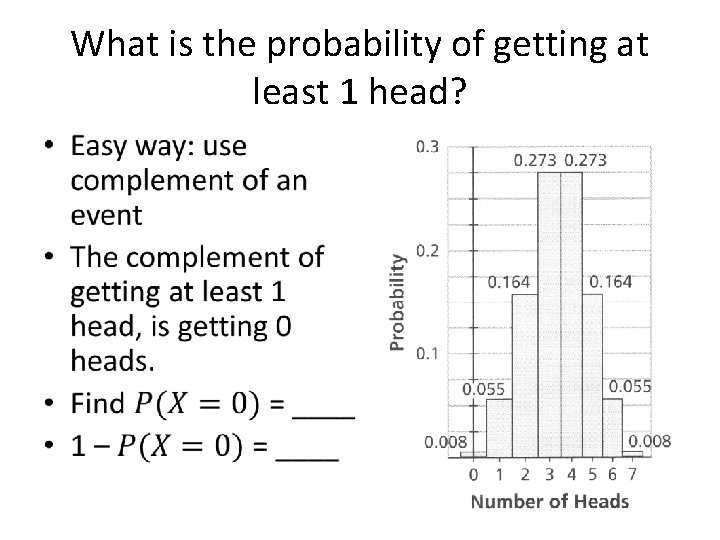
What is the probability of getting at least 1 head? •

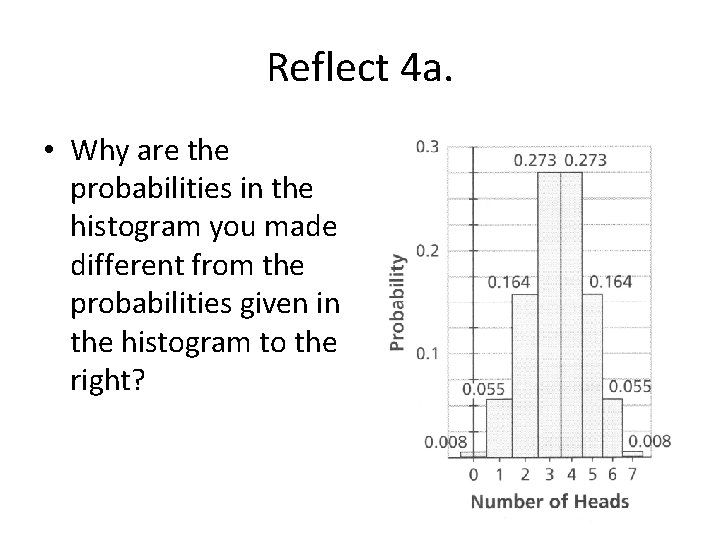
Reflect 4 a. • Why are the probabilities in the histogram you made different from the probabilities given in the histogram to the right?

Reflect 4 b. • What do you think would happen to the histogram you made in our trials if you included data from 1000 additional trials?

Reflect 4 c. • Why does it make sense that the histogram that shows theoretical probabilities is symmetric?