Probability Distribution v Random Variable A variable with
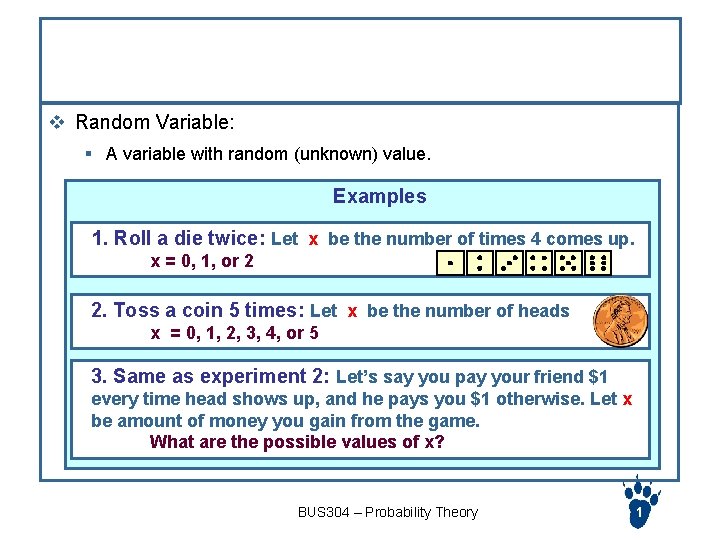
Probability Distribution v Random Variable: § A variable with random (unknown) value. Examples 1. Roll a die twice: Let x be the number of times 4 comes up. x = 0, 1, or 2 2. Toss a coin 5 times: Let x be the number of heads x = 0, 1, 2, 3, 4, or 5 3. Same as experiment 2: Let’s say you pay your friend $1 every time head shows up, and he pays you $1 otherwise. Let x be amount of money you gain from the game. What are the possible values of x? BUS 304 – Probability Theory 1
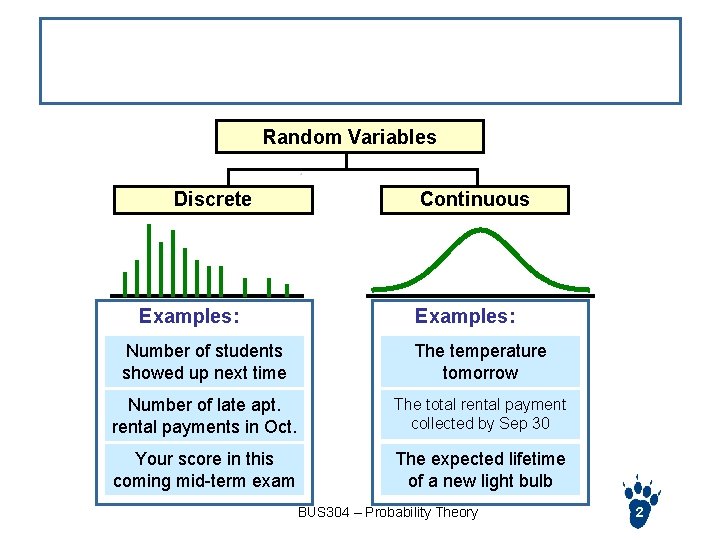
Discrete vs. Continuous Random variables Random Variables Discrete Examples: Continuous Examples: Number of students showed up next time The temperature tomorrow Number of late apt. rental payments in Oct. The total rental payment collected by Sep 30 Your score in this coming mid-term exam The expected lifetime of a new light bulb BUS 304 – Probability Theory 2
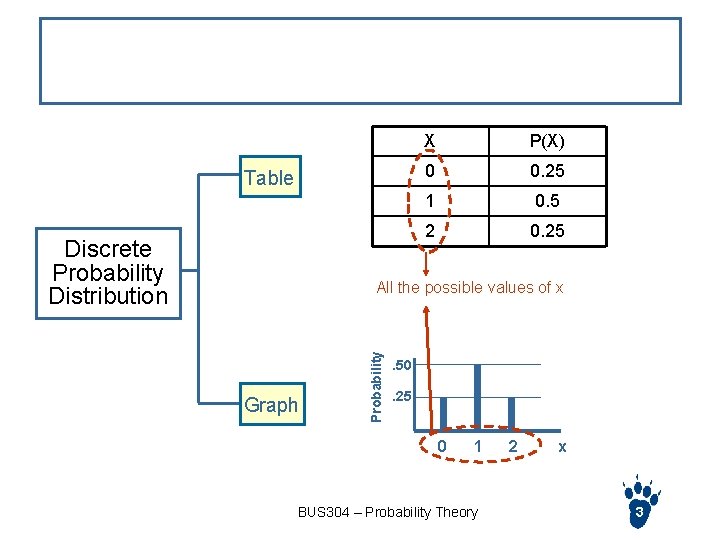
Discrete Probability Distribution Table Discrete Probability Distribution X P(X) 0 0. 25 1 0. 5 2 0. 25 Graph Probability All the possible values of x . 50. 25 0 1 BUS 304 – Probability Theory 2 x 3

Exercise v Describe the probability distribution of the following experiments: § Draw a pair of dice, x is the random variable representing the sum of the total points. § In a community with 100 households, 10 do not have kid, 40 have just one kid, 30 have 2 kids, and 20 have 3 kids. Randomly select one household. Let X be the number of kids in the household. BUS 304 – Probability Theory 4

Measures of Discrete Random Variables v Expected value of a discrete distribution § An weighted average, taking into account the probability § The expected value of random variable x is denoted as E(x)= xi P(xi) E(x)= x 1 P(x 1) +x 2 P(x 2) + … + xn. P(xn) Example: What is your expected gain when you play the flip-coin game twice? x -2 0 2 P(x). 25. 50. 25 E(x) = (-2) * 0. 25 + 0 * 0. 5 + 2 * 0. 25 =0 Your expected gain is 0! – a fair game. BUS 304 – Probability Theory 5
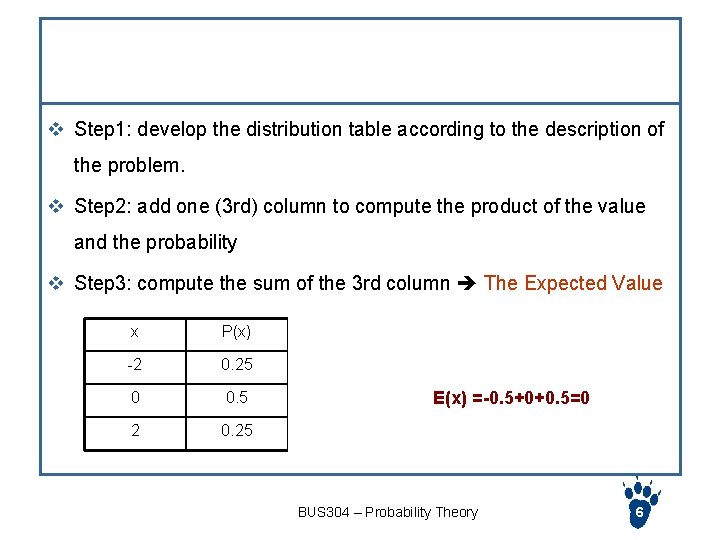
Worksheet to compute the expected value v Step 1: develop the distribution table according to the description of the problem. v Step 2: add one (3 rd) column to compute the product of the value and the probability v Step 3: compute the sum of the 3 rd column The Expected Value x P(x) x*P(x) -2 0. 25 -2*. 25=-0. 5 0*0. 5=0 2 0. 25 2*0. 25=0. 5 E(x) =-0. 5+0+0. 5=0 BUS 304 – Probability Theory 6
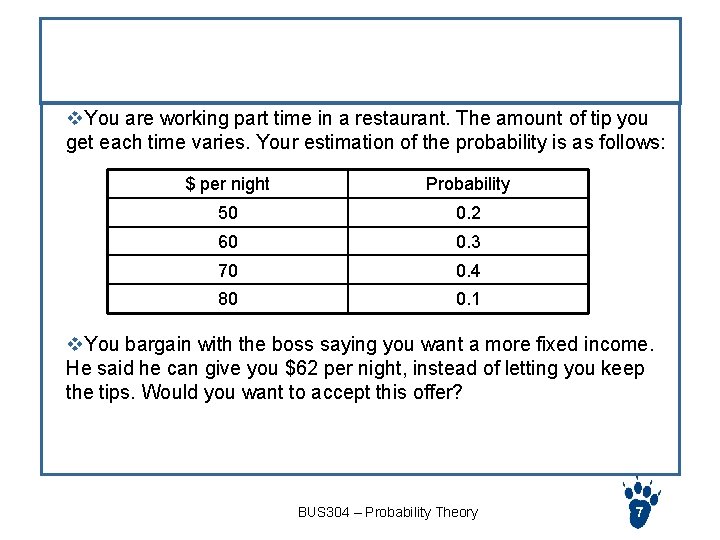
Exercise v. You are working part time in a restaurant. The amount of tip you get each time varies. Your estimation of the probability is as follows: $ per night Probability 50 0. 2 60 0. 3 70 0. 4 80 0. 1 v. You bargain with the boss saying you want a more fixed income. He said he can give you $62 per night, instead of letting you keep the tips. Would you want to accept this offer? BUS 304 – Probability Theory 7

More exercise v What is the expected gain if you plan the flip coin game just once? § Three times? § Four Times? v What is the expected number of kid in that community (see the example on page 4)? BUS 304 – Probability Theory 8

Rule for expected value v If there are two random variables, x and y. Then E(x+y) = E(x) + E(y) § Example: • x is your gain from the flip-coin game the first time • y is your gain from the flip-coin game the second time • x+y is your total gain from playing the game twice. x P(x) y P(y) x+y P(x+y) -1 0. 5 -2 0. 25 1 0. 5 0 0. 5 2 0. 25 E(x)=0 E(y)=0 BUS 304 – Probability Theory E(x+y)=0 9
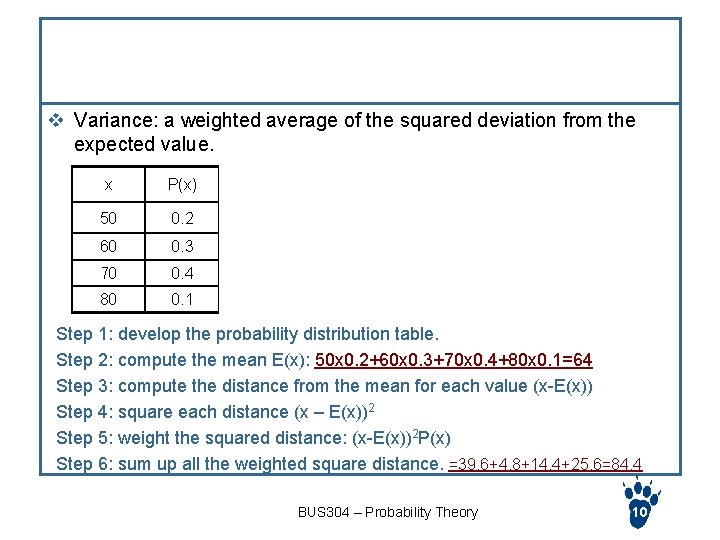
Measures – variance v Variance: a weighted average of the squared deviation from the expected value. x P(x) x – E(x) (x-E(x))2 P(x) 50 0. 2 50 -64=-$14 (-14)2=196 196*0. 2=39. 6 60 0. 3 -$4 16 4. 8 70 0. 4 $6 36 14. 4 80 0. 1 $16 25. 6 Step 1: develop the probability distribution table. Step 2: compute the mean E(x): 50 x 0. 2+60 x 0. 3+70 x 0. 4+80 x 0. 1=64 Step 3: compute the distance from the mean for each value (x-E(x)) Step 4: square each distance (x – E(x))2 Step 5: weight the squared distance: (x-E(x))2 P(x) Step 6: sum up all the weighted square distance. =39. 6+4. 8+14. 4+25. 6=84. 4 BUS 304 – Probability Theory 10

Variance and Standard deviation v variance § The variance of a random variable has the same meaning as the variance of population § Calculation is the same as calculating population v Standard deviation of a random variable: § Same of the population standard deviation § Calculate the variance § Then take the square root of the variance. § Written as SD(x) or variance using a relative frequency table. e. g. for the example on page 10 § Written as var(x) or BUS 304 – Probability Theory 11
Homework v Problem 4. 40 v Problem 4. 50 BUS 304 – Probability Theory 12
- Slides: 12