Probability distribution functions Normal distribution Lognormal distribution Mean

Probability distribution functions • • • Normal distribution Lognormal distribution Mean, median and mode Tails Extreme value distributions

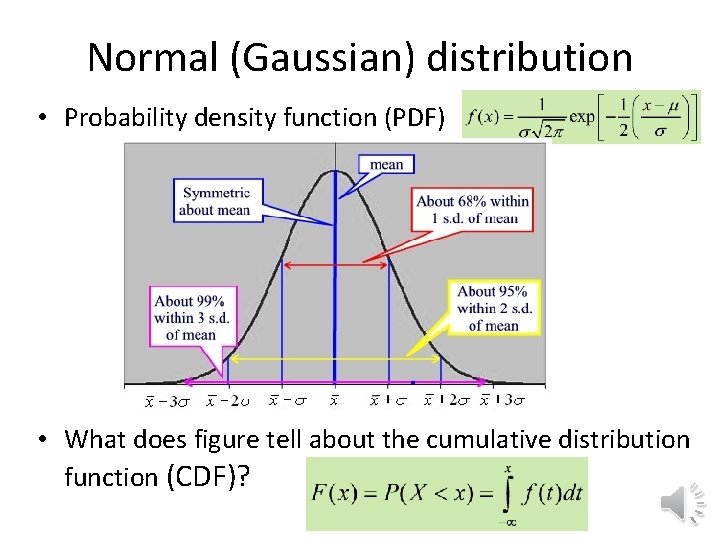
Normal (Gaussian) distribution • Probability density function (PDF) • What does figure tell about the cumulative distribution function (CDF)?

More on the normal distribution •

Estimating mean and standard deviation • Given a sample from a normally distributed variable, the sample mean is the best linear unbiased estimator (BLUE) of the true mean. • For the variance the equation gives the best unbiased estimator, but the square root is not an unbiased estimate of the standard deviation • For example, for a sample of 5 from a standard normal distribution, the standard deviation will be estimated on average as 0. 94 (with standard deviation of 0. 34)

Lognormal distribution •

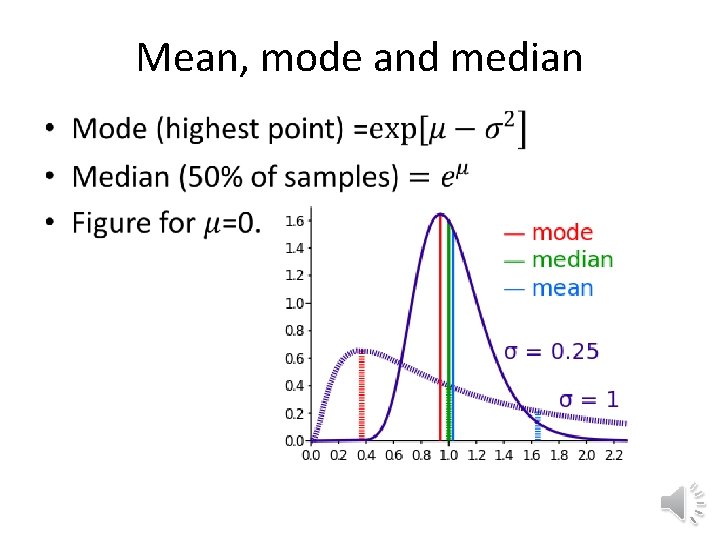
Mean, mode and median •

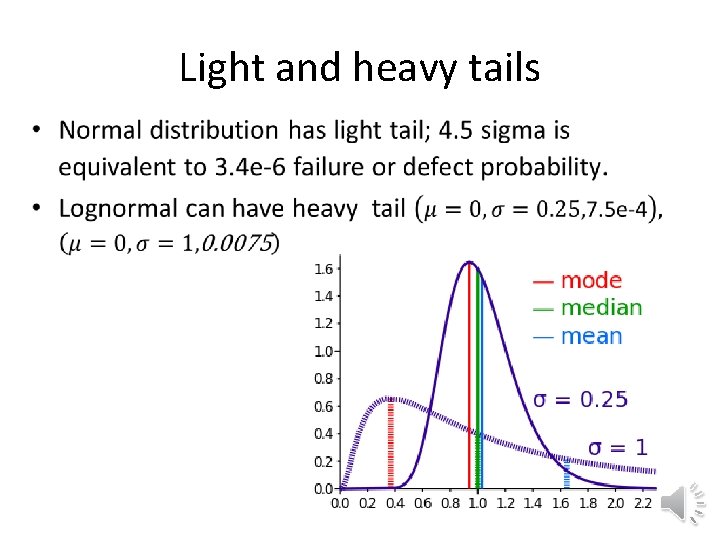
Light and heavy tails •

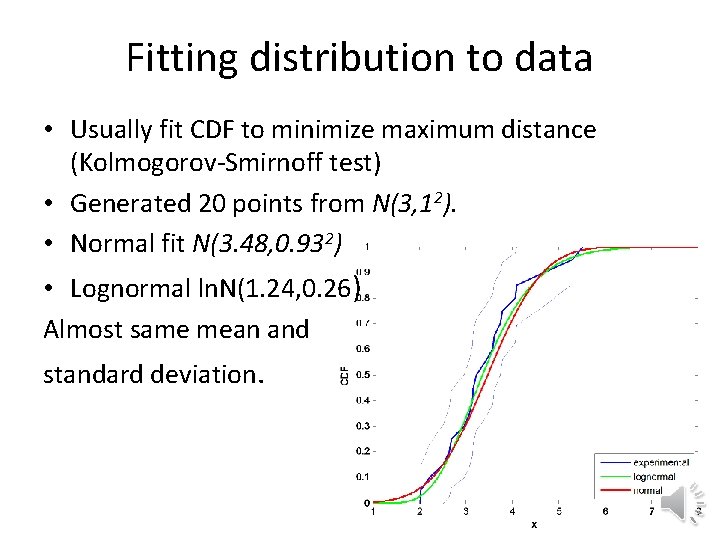
Fitting distribution to data • Usually fit CDF to minimize maximum distance (Kolmogorov-Smirnoff test) • Generated 20 points from N(3, 12). • Normal fit N(3. 48, 0. 932) • Lognormal ln. N(1. 24, 0. 26) Almost same mean and standard deviation.

Extreme value distributions • No matter what distribution you sample from, the mean of the sample tends to be normally distributed as sample size increases (what mean and standard deviation? ) • Similarly, distributions of the minimum (or maximum) of samples belong to other distributions. • Even though there are infinite number of distributions, there are only three extreme value distribution. – Type I (Gumbel) derived from normal. – Type II (Frechet) e. g. maximum daily rainfall – Type III (Weibull) weakest link failure

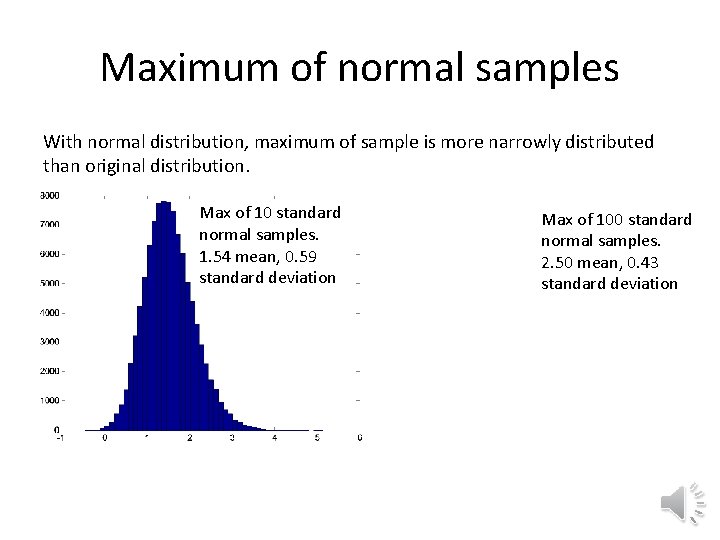
Maximum of normal samples With normal distribution, maximum of sample is more narrowly distributed than original distribution. Max of 10 standard normal samples. 1. 54 mean, 0. 59 standard deviation Max of 100 standard normal samples. 2. 50 mean, 0. 43 standard deviation

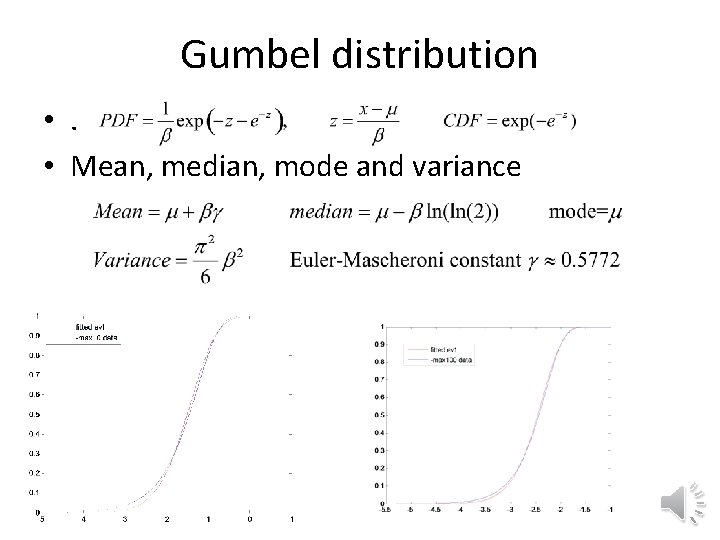
Gumbel distribution • . • Mean, median, mode and variance

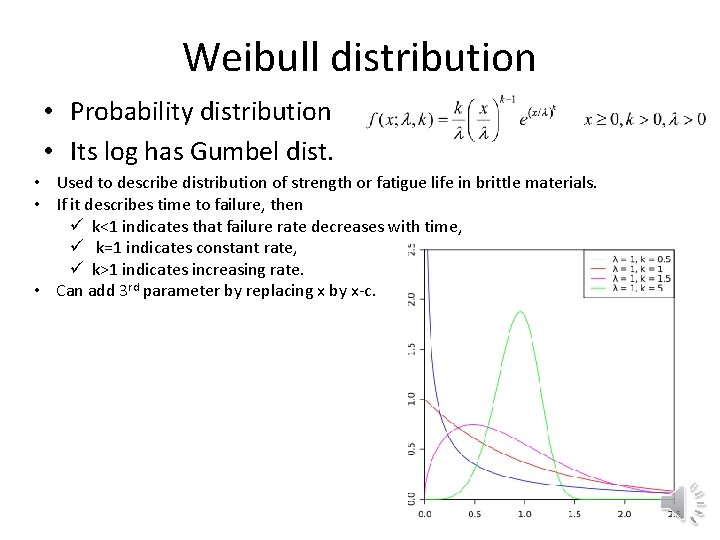
Weibull distribution • Probability distribution • Its log has Gumbel dist. • Used to describe distribution of strength or fatigue life in brittle materials. • If it describes time to failure, then ü k<1 indicates that failure rate decreases with time, ü k=1 indicates constant rate, ü k>1 indicates increasing rate. • Can add 3 rd parameter by replacing x by x-c.

Exercises • Find how many samples of normally distributed numbers you need in order to estimate the mean and standard deviation with an error that will be less than 10% of the true standard deviation most of the time. • Both the lognormal and Weibull distributions are used to model strength. Find how closely you can approximate data generated from a standard lognormal distribution by fitting it with Weibull. • Take the introduction and preamble of the US Declaration of Independence, and fit the distribution of word lengths using the K-S criterion. What distribution fits best? Compare the graphs of the CDFs. Compare to a more contemporary text.