Probability Discussion Topics Conditional Probability Probability using the

Probability

Discussion Topics § Conditional Probability § Probability using the general multiplication rule § Independent event

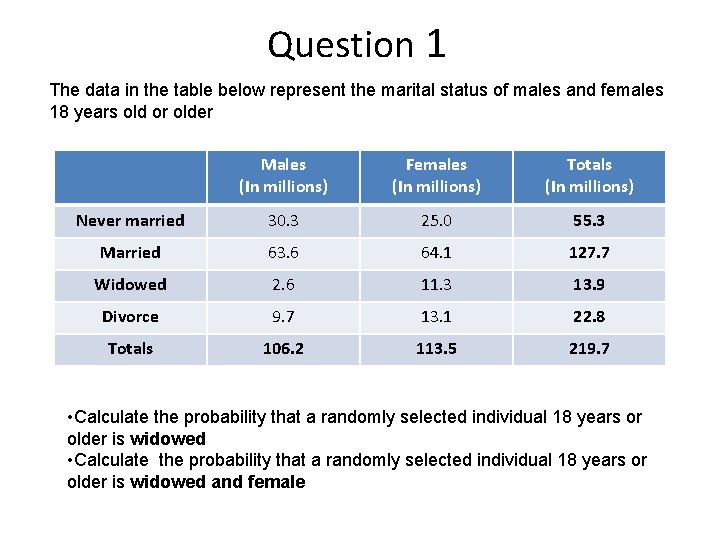
Question 1 The data in the table below represent the marital status of males and females 18 years old or older Males (In millions) Females (In millions) Totals (In millions) Never married 30. 3 25. 0 55. 3 Married 63. 6 64. 1 127. 7 Widowed 2. 6 11. 3 13. 9 Divorce 9. 7 13. 1 22. 8 Totals 106. 2 113. 5 219. 7 • Calculate the probability that a randomly selected individual 18 years or older is widowed and female

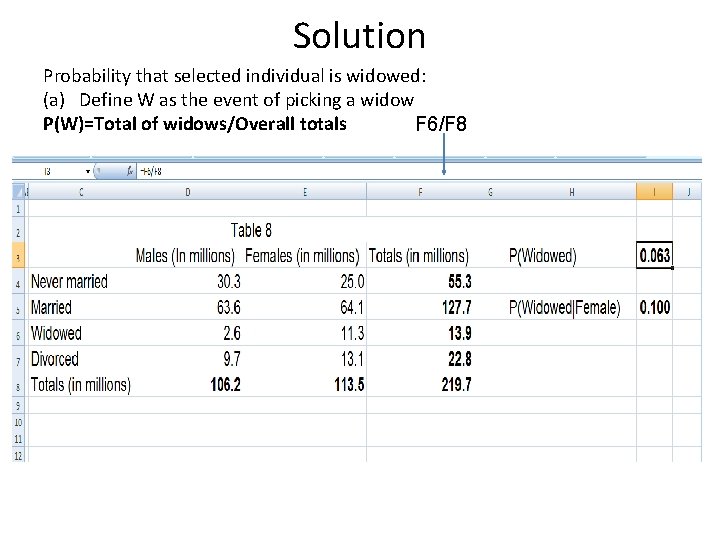
Solution Probability that selected individual is widowed: (a) Define W as the event of picking a widow P(W)=Total of widows/Overall totals F 6/F 8

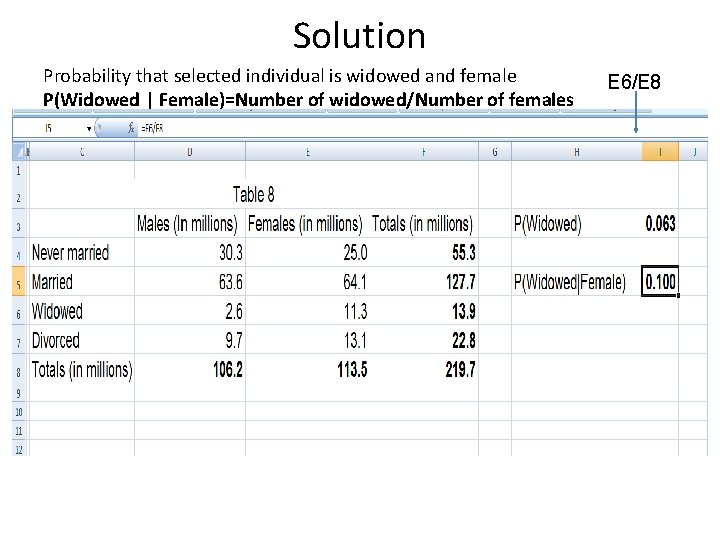
Solution Probability that selected individual is widowed and female P(Widowed | Female)=Number of widowed/Number of females E 6/E 8

Question 2 In the game of roulette, the wheel has slots numbered 0, 00, and 1 through 36. A metal ball is allowed to roll around a wheel until it falls into one of the numbered slots. You decide to play the game and place a bet on the number 17. (a) What is the probability that the ball will land in the slot numbered 17 two times in a row?

Solution (1/38)/(1/38) The events are independent because the probability of the 1 st spin cannot affect the probability of the second spin. The ball does not remember it landed on 17 on the first spin

Question 3 Suppose that a box of 100 circuits is sent to a manufacturing plant. Of the 100 circuits shipped, 5 are defective. The plant manager receiving the circuits randomly selects 2 and tests them. If both circuits work, she will accept the shipment. Otherwise the shipment is rejected. (a) Use a tree diagram to represent all possible outcomes (b) What is the probability that the plant manager discovers at least 1 defective circuit and rejects the shipment

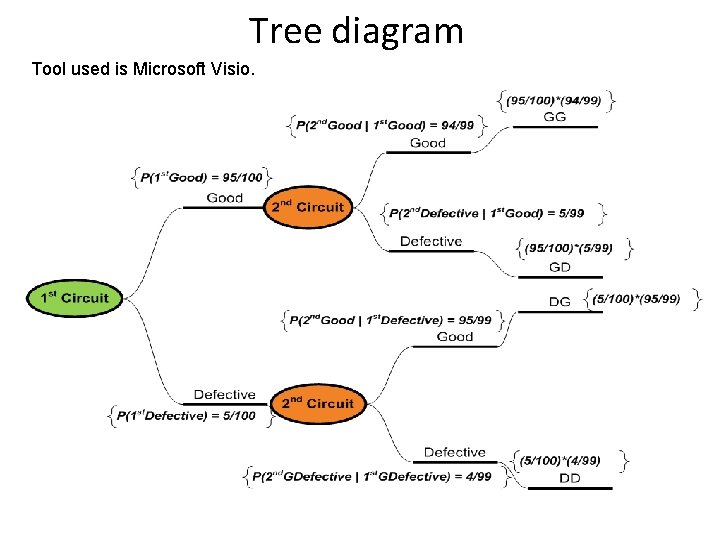
Tree diagram Tool used is Microsoft Visio.

From our tree diagram and using addition rule: P(at least 1 defective) = P(GD) + P(DG) + P(DD) = 0. 048+0. 002 = 0. 098 There is 0. 098 probability of shipment being rejected 2 nd Approach: P(at least 1 defective) = 1 -P(none defective) = 1 - (95/100)*(94/99) = 1 - 0. 902 = 0. 098

CSTEM Web link http: //www. cis. famu. edu/~cdellor/math/ § § Presentation slides Problems Guidelines Learning materials