Probability Density Function pdf Relative frequency Large sample

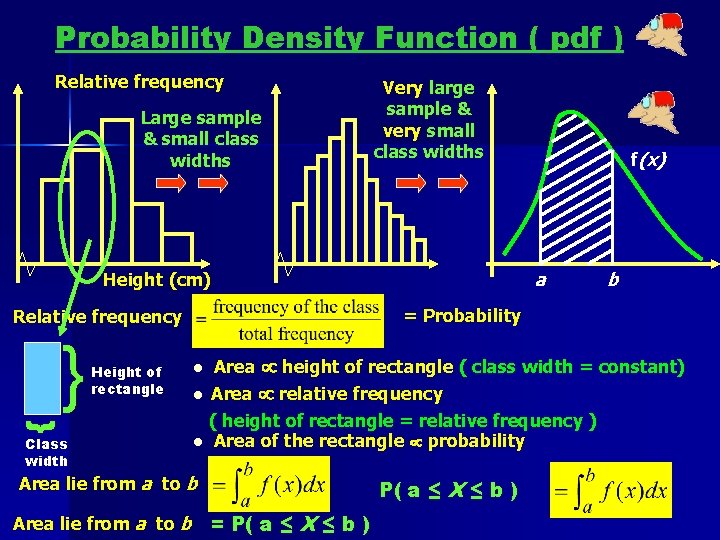
Probability Density Function ( pdf ) Relative frequency Large sample & small class widths Very large sample & very small class widths a Height (cm) } } Class width Area height of rectangle ( class width = constant) l Area relative frequency ( height of rectangle = relative frequency ) l Area of the rectangle probability l Area lie from a to b b = Probability Relative frequency Height of rectangle f(x) P( a ≤ X ≤ b ) = P( a ≤ X ≤ b )

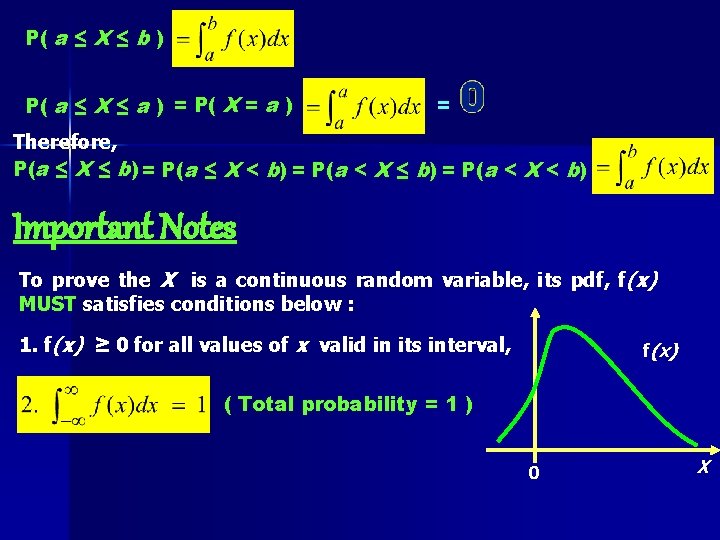
P( a ≤ X ≤ b ) P( a ≤ X ≤ a ) = P( X = a ) = Therefore, P(a ≤ X ≤ b) = P(a ≤ X < b) = P(a < X ≤ b) = P(a < X < b) Important Notes To prove the X is a continuous random variable, its pdf, f(x) MUST satisfies conditions below : 1. f(x) ≥ 0 for all values of x valid in its interval, f(x) ( Total probability = 1 ) 0 X

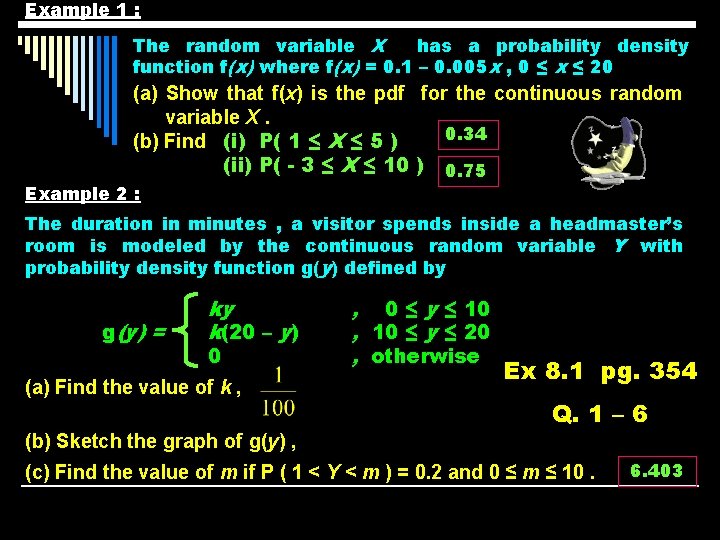
Example 1 : The random variable X has a probability density function f(x) where f(x) = 0. 1 – 0. 005 x , 0 ≤ x ≤ 20 (a) Show that f(x) is the pdf for the continuous random variable X. 0. 34 (b) Find (i) P( 1 ≤ X ≤ 5 ) (ii) P( - 3 ≤ X ≤ 10 ) 0. 75 Example 2 : The duration in minutes , a visitor spends inside a headmaster’s room is modeled by the continuous random variable Y with probability density function g(y) defined by g(y) = ky k(20 – y) 0 (a) Find the value of k , , 0 ≤ y ≤ 10 , 10 ≤ y ≤ 20 , otherwise Ex 8. 1 pg. 354 Q. 1 – 6 (b) Sketch the graph of g(y) , (c) Find the value of m if P ( 1 < Y < m ) = 0. 2 and 0 ≤ m ≤ 10. 6. 403

Example 3 : The continuous random variable X has a probability density function f(x) where , 0 ≤ x ≤ 10 f(x) = ( a ) If P ( X ≥a ) = 0 , find the value a. ( b ) Find the median of X. 2. 93 Example 4 : , otherwise 8 Ex 8. 1 pg. 355 Q. 7 – 10 The continuous random variable X has a probability density function f(x) where , 0≤x≤ 4 f(x) = , 4 ≤ x ≤ 12 0 , otherwise 5. 07 ( a ) Find the median of X. ( b ) Find the first quartile and third quartile of X. ( c ) If P ( X < a ) = 0. 1 , find the value a.