Probability Densities in Data Mining Andrew W Moore
Probability Densities in Data Mining Andrew W. Moore Professor School of Computer Science Carnegie Mellon University www. cs. cmu. edu/~awm awm@cs. cmu. edu 412 -268 -7599 Copyright © Andrew W. Moore Slide 1
Contenido • • Porque son importantes. Notacion y fundamentos de PDF continuas. PDFs multivariadas continuas. Combinando variables aleatorias discretas y continuas. Copyright © Andrew W. Moore Slide 2
Porque son importantes? • • • Real Numbers occur in at least 50% of database records Can’t always quantize them So need to understand how to describe where they come from A great way of saying what’s a reasonable range of values A great way of saying how multiple attributes should reasonably co-occur Copyright © Andrew W. Moore Slide 3
Porque son importantes? • • • Can immediately get us Bayes Classifiers that are sensible with real-valued data You’ll need to intimately understand PDFs in order to do kernel methods, clustering with Mixture Models, analysis of variance, time series and many other things Will introduce us to linear and non-linear regression Copyright © Andrew W. Moore Slide 4
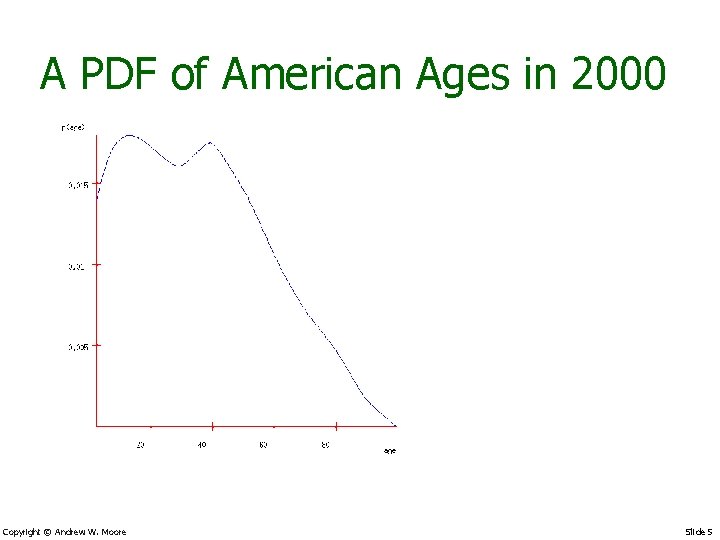
A PDF of American Ages in 2000 Copyright © Andrew W. Moore Slide 5
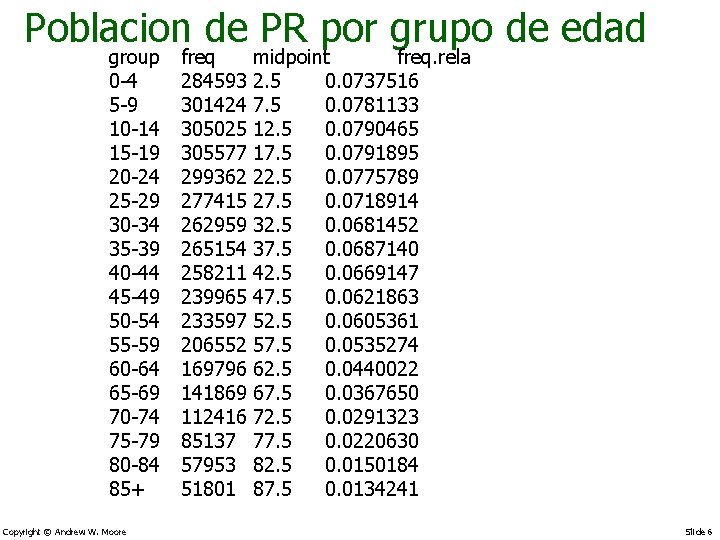
Poblacion de PR por grupo de edad group 0 -4 5 -9 10 -14 15 -19 20 -24 25 -29 30 -34 35 -39 40 -44 45 -49 50 -54 55 -59 60 -64 65 -69 70 -74 75 -79 80 -84 85+ Copyright © Andrew W. Moore freq 284593 301424 305025 305577 299362 277415 262959 265154 258211 239965 233597 206552 169796 141869 112416 85137 57953 51801 midpoint freq. rela 2. 5 0. 0737516 7. 5 0. 0781133 12. 5 0. 0790465 17. 5 0. 0791895 22. 5 0. 0775789 27. 5 0. 0718914 32. 5 0. 0681452 37. 5 0. 0687140 42. 5 0. 0669147 47. 5 0. 0621863 52. 5 0. 0605361 57. 5 0. 0535274 62. 5 0. 0440022 67. 5 0. 0367650 72. 5 0. 0291323 77. 5 0. 0220630 82. 5 0. 0150184 87. 5 0. 0134241 Slide 6
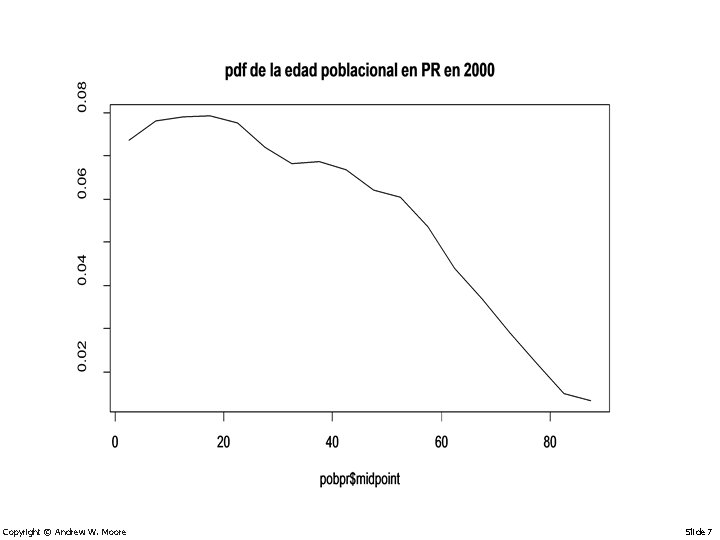
Copyright © Andrew W. Moore Slide 7
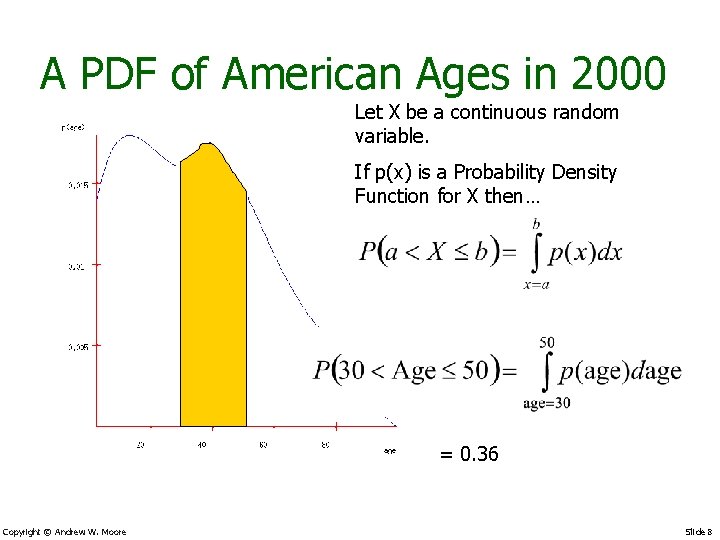
A PDF of American Ages in 2000 Let X be a continuous random variable. If p(x) is a Probability Density Function for X then… = 0. 36 Copyright © Andrew W. Moore Slide 8
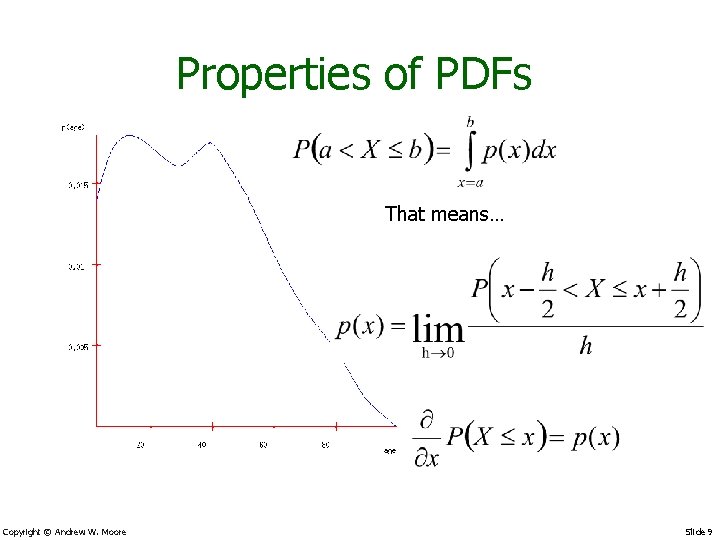
Properties of PDFs That means… Copyright © Andrew W. Moore Slide 9
Donde x-h/2<w<x+h/2). Luego, Asi p(w) tiende a p(x) cuando h tiende a cero Copyright © Andrew W. Moore Slide 10
Funcion de distribucion acumulativa. Esta es una funcion No decreciente Notar que p(w) tiende a p(x) cuando h tiende a 0 Se ha mostrado que la derivada de la funcion de distribucion da la funcion de densidad Copyright © Andrew W. Moore Slide 11
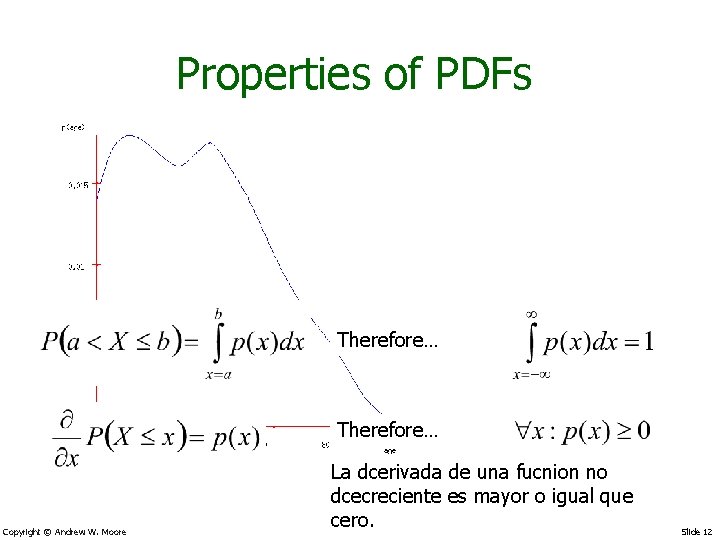
Properties of PDFs Therefore… Copyright © Andrew W. Moore La dcerivada de una fucnion no dcecreciente es mayor o igual que cero. Slide 12
• Cual es el significado de p(x)? Si p(5. 31) = 0. 06 and p(5. 92) = 0. 03 Entonces cuando un valor de X es muestreado de la distribucion, es dos veces mas probable que X este mas cerca a 5. 31 que a 5. 92. Copyright © Andrew W. Moore Slide 13
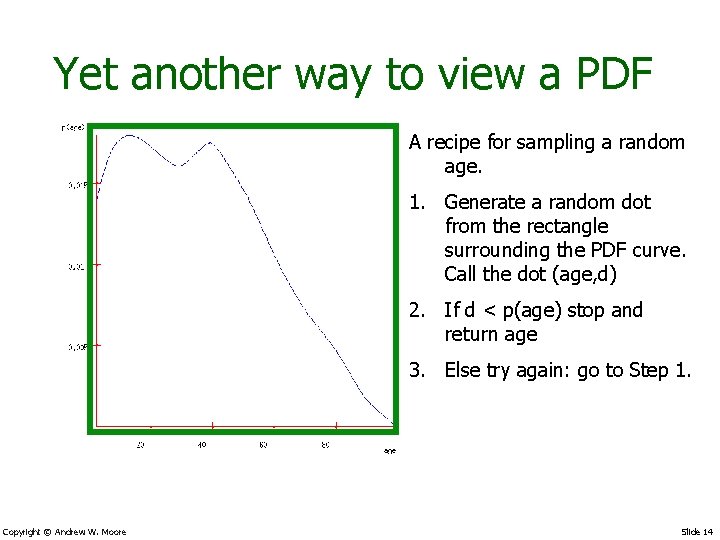
Yet another way to view a PDF A recipe for sampling a random age. 1. Generate a random dot from the rectangle surrounding the PDF curve. Call the dot (age, d) 2. If d < p(age) stop and return age 3. Else try again: go to Step 1. Copyright © Andrew W. Moore Slide 14
Test your understanding • True or False: Copyright © Andrew W. Moore Slide 15
![Expectations E[X] = the expected value of random variable X = the average value](http://slidetodoc.com/presentation_image_h/0be08d797e33b982297acce6e8a8cb6e/image-16.jpg "Expectations E[X] = the expected value of random variable X = the average value")
Expectations E[X] = the expected value of random variable X = the average value we’d see if we took a very large number of random samples of X Copyright © Andrew W. Moore Slide 16
![Expectations E[X] = the expected value of random variable X = the average value](http://slidetodoc.com/presentation_image_h/0be08d797e33b982297acce6e8a8cb6e/image-17.jpg "Expectations E[X] = the expected value of random variable X = the average value")
Expectations E[X] = the expected value of random variable X = the average value we’d see if we took a very large number of random samples of X E[age]=35. 897 = the first moment of the shape formed by the axes and the blue curve = the best value to choose if you must guess an unknown person’s age and you’ll be fined the square of your error Copyright © Andrew W. Moore Slide 17
![Expectation of a function =E[f(X)] = the expected value of f(x) where x is](http://slidetodoc.com/presentation_image_h/0be08d797e33b982297acce6e8a8cb6e/image-18.jpg "Expectation of a function =E[f(X)] = the expected value of f(x) where x is")
Expectation of a function =E[f(X)] = the expected value of f(x) where x is drawn from X’s distribution. = the average value we’d see if we took a very large number of random samples of f(X) Note that in general: Copyright © Andrew W. Moore Slide 18
![Variance s 2 = Var[X] = the expected squared difference between x and E[X]](http://slidetodoc.com/presentation_image_h/0be08d797e33b982297acce6e8a8cb6e/image-19.jpg "Variance s 2 = Var[X] = the expected squared difference between x and E[X]")
Variance s 2 = Var[X] = the expected squared difference between x and E[X] = amount you’d expect to lose if you must guess an unknown person’s age and you’ll be fined the square of your error, and assuming you play optimally Copyright © Andrew W. Moore Slide 19
![Standard Deviation s = Var[X] = the 2 expected squared difference between x and](http://slidetodoc.com/presentation_image_h/0be08d797e33b982297acce6e8a8cb6e/image-20.jpg "Standard Deviation s = Var[X] = the 2 expected squared difference between x and")
Standard Deviation s = Var[X] = the 2 expected squared difference between x and E[X] = amount you’d expect to lose if you must guess an unknown person’s age and you’ll be fined the square of your error, and assuming you play optimally s = Standard Deviation = “typical” deviation of X from its mean Copyright © Andrew W. Moore Slide 20
Estadisticas para PR • • • E(edad)=35. 17 Var(edad)=501. 16 Desv. Est(edad)=22. 38 Copyright © Andrew W. Moore Slide 21
Funciones de densidad mas conocidas Copyright © Andrew W. Moore Slide 22
Funciones de densidad mas conocidas • • La densidad uniforme o rectangular La densidad triangular La densidad exponencial La densidad Gamma y la Chi-square La densidad Beta La densidad Normal o Gaussiana Las densidades t y F. Copyright © Andrew W. Moore Slide 23
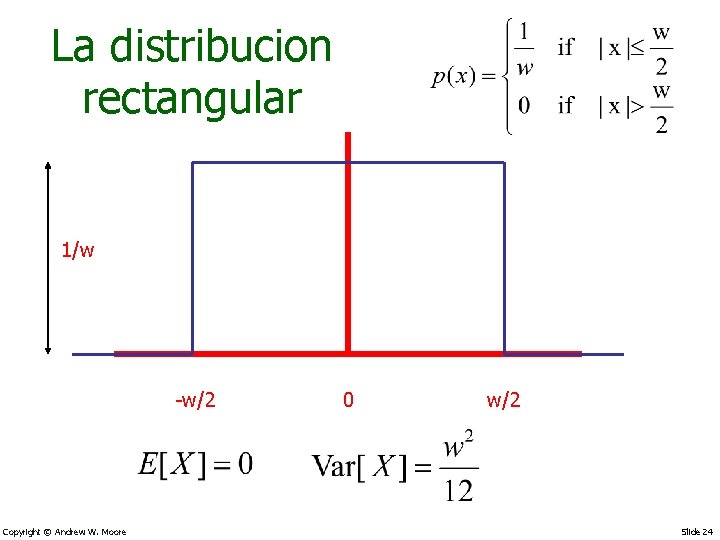
La distribucion rectangular 1/w -w/2 Copyright © Andrew W. Moore 0 w/2 Slide 24
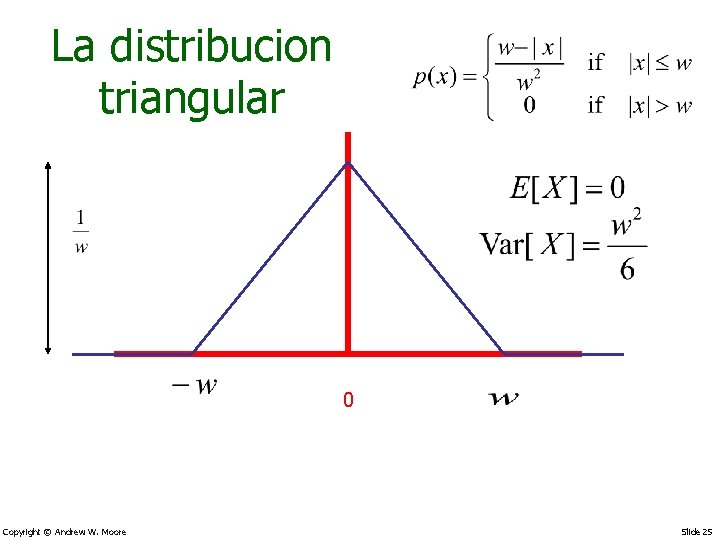
La distribucion triangular 0 Copyright © Andrew W. Moore Slide 25
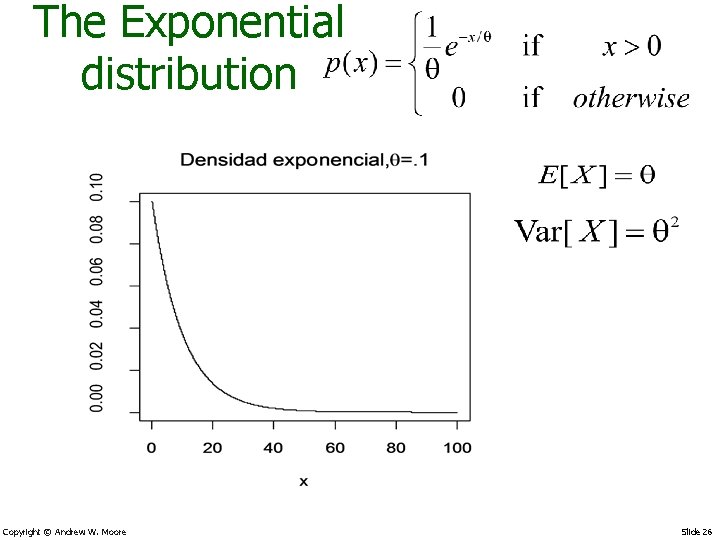
The Exponential distribution Copyright © Andrew W. Moore Slide 26
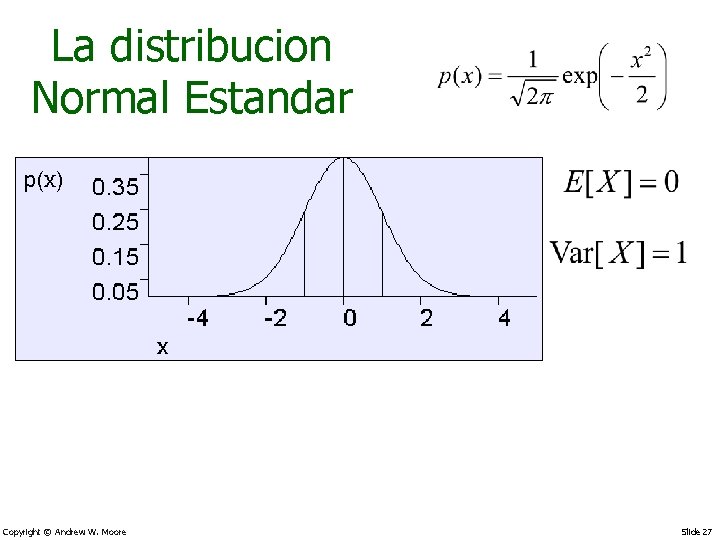
La distribucion Normal Estandar Copyright © Andrew W. Moore Slide 27
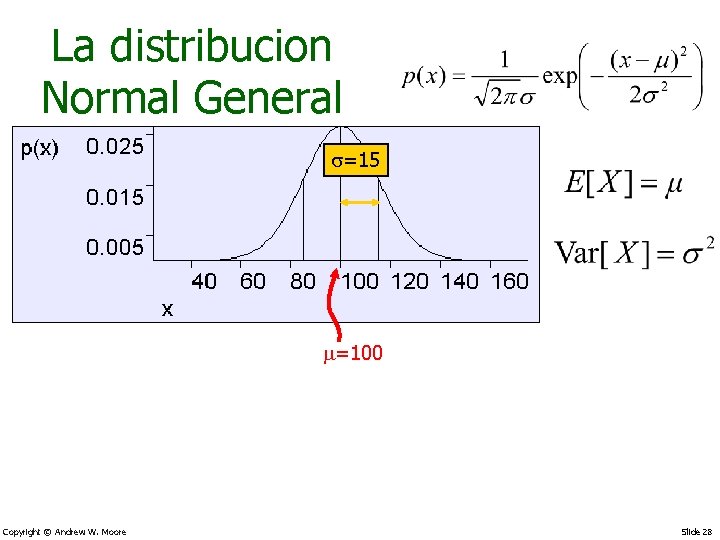
La distribucion Normal General s=15 =100 Copyright © Andrew W. Moore Slide 28
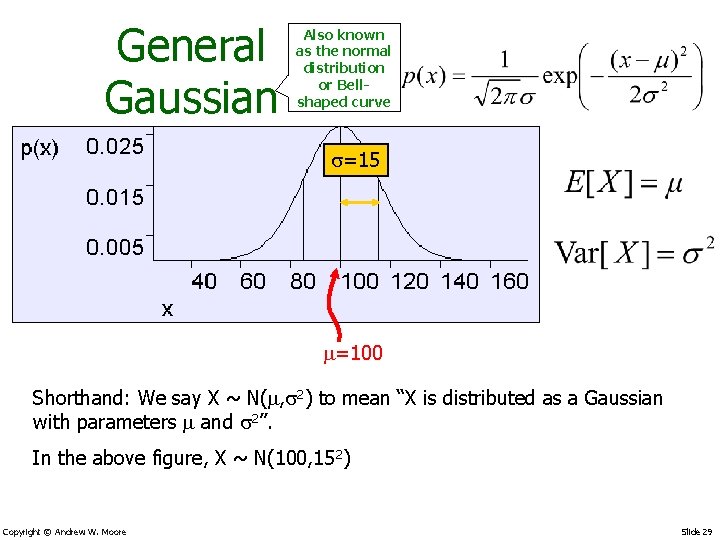
General Gaussian Also known as the normal distribution or Bellshaped curve s=15 =100 Shorthand: We say X ~ N( , s 2) to mean “X is distributed as a Gaussian with parameters and s 2”. In the above figure, X ~ N(100, 152) Copyright © Andrew W. Moore Slide 29
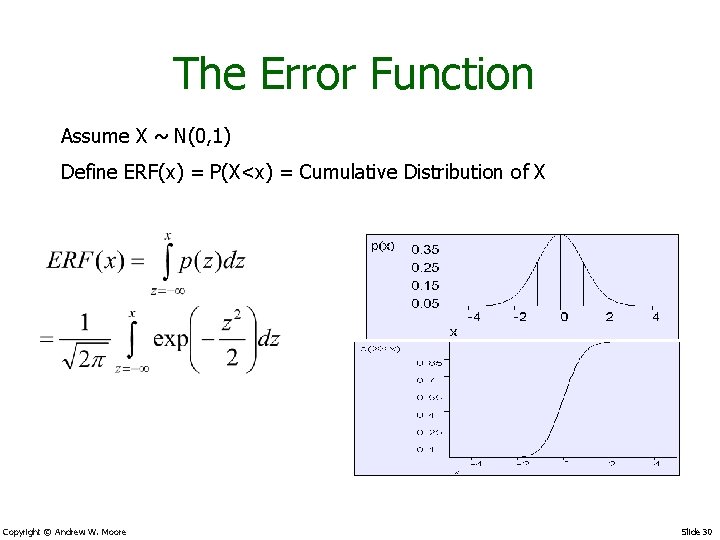
The Error Function Assume X ~ N(0, 1) Define ERF(x) = P(X<x) = Cumulative Distribution of X Copyright © Andrew W. Moore Slide 30
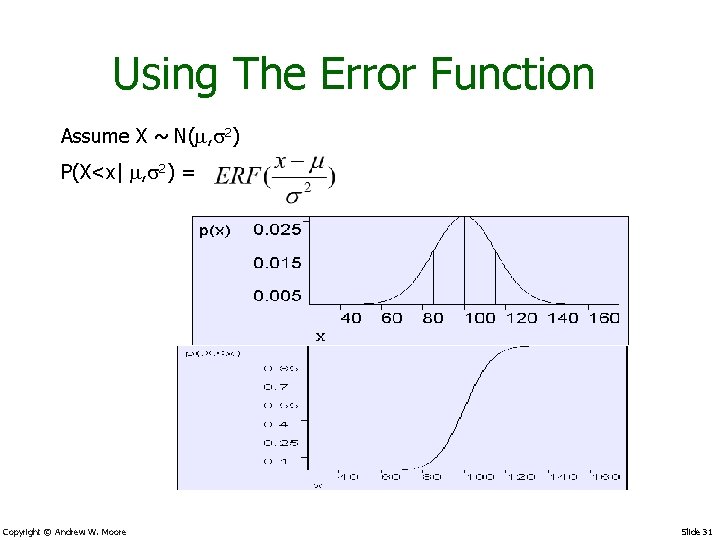
Using The Error Function Assume X ~ N( , s 2) P(X<x| , s 2) = Copyright © Andrew W. Moore Slide 31
The Central Limit Theorem • • • If (X 1, X 2, … Xn) are i. i. d. continuous random variables Then define As n-->infinity, p(z)--->Gaussian with mean E[Xi] and variance Var[Xi] Somewhat of a justification for assuming Gaussian noise is common Copyright © Andrew W. Moore Slide 32
Estimadores de funcion de densidad Histograms h ancho de clase • K-nearest neighbors: dk es la distancia hasta el k-esimo vecino • Kernel density estimators • Copyright © Andrew W. Moore Slide 33
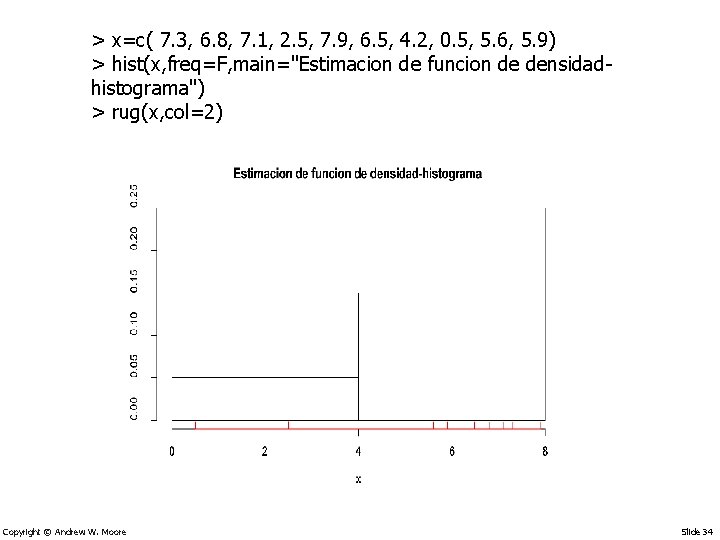
> x=c( 7. 3, 6. 8, 7. 1, 2. 5, 7. 9, 6. 5, 4. 2, 0. 5, 5. 6, 5. 9) > hist(x, freq=F, main="Estimacion de funcion de densidadhistograma") > rug(x, col=2) Copyright © Andrew W. Moore Slide 34
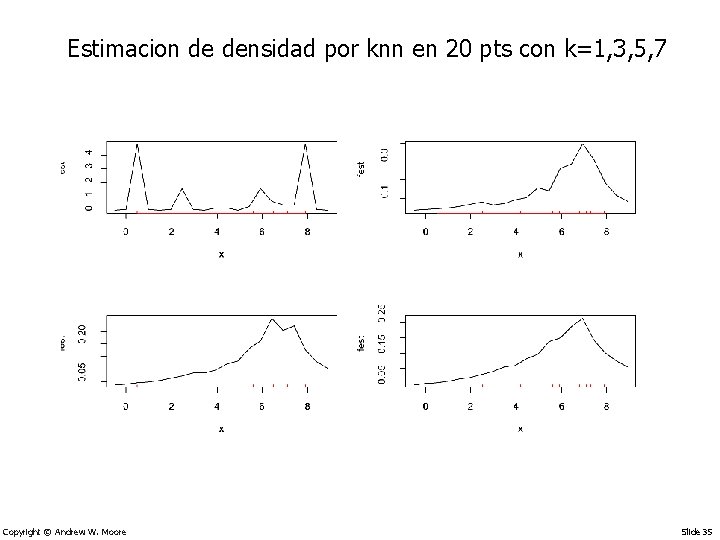
Estimacion de densidad por knn en 20 pts con k=1, 3, 5, 7 Copyright © Andrew W. Moore Slide 35
Estimación por kernels de una función de densidad univariada. En el caso univariado, el estimador por kernels de la función de densidad f(x) se obtiene de la siguiente manera. Consideremos que x 1, …xn es una variable aleatoria X con función de densidad f(x), definamos la función de distribución empirica por el cual es un estimador de la función de distribución acumulada F(x) de X. Considerando que la función de densidad f(x) es la derivada de la función de distribución F y usando aproximación para derivada se tiene que Copyright © Andrew W. Moore Slide 36
donde h es un valor positivo cercano a cero. Lo anterior es equivalente a la proporción de puntos en el intervalo (x-h, x+h) dividido por 2 h. La ecuación anterior puede ser escrita como: donde la función peso K está definida por 0 si |z|>1 K(z)= 1/2 si |z| 1 Copyright © Andrew W. Moore Slide 37
Muestra: 6, 8, 9 12, 20, 25, 18, 31 Copyright © Andrew W. Moore Slide 38
este es llamado el kernel uniforme y h es llamado el ancho de banda el cual es un parámetro de suavización que indica cuanto contribuye cada punto muestral al estimado en el punto x. En general, K y h deben satisfacer ciertas condiciones de regularidad, tales como: K(z) debe ser acotado y absolutamente integrable en (- , ) Usualmente, pero no siempre, K(z) 0 y simétrico, luego cualquier función de densidad simétrica puede usarse como kernel. Copyright © Andrew W. Moore Slide 39
Eleccion del ancho de banda h Donde n es el numero de datos y s la desviacion estandar de la muestra. Copyright © Andrew W. Moore Slide 40
EL KERNEL GAUSSIANO En este caso el kernel representa una función peso más suave donde todos los puntos contribuyen al estimado de f(x) en x. Es decir, Copyright © Andrew W. Moore Slide 41
EL KERNEL TRIANGULAR K(z)=1 - |z| para |z|<1, 0 en otro caso. EL KERNEL "BIWEIGHT" 15/16(1 -z 2)2 para |z|<1 0 en otro caso K(z)= Copyright © Andrew W. Moore Slide 42
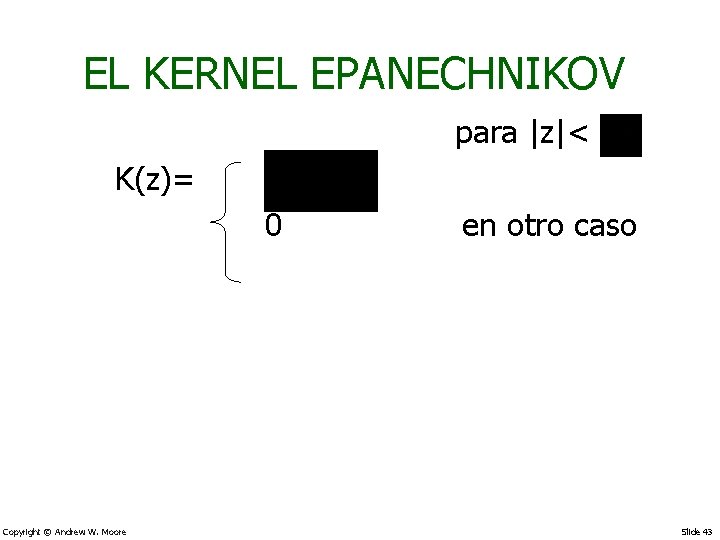
EL KERNEL EPANECHNIKOV para |z|< K(z)= 0 en otro caso Copyright © Andrew W. Moore Slide 43
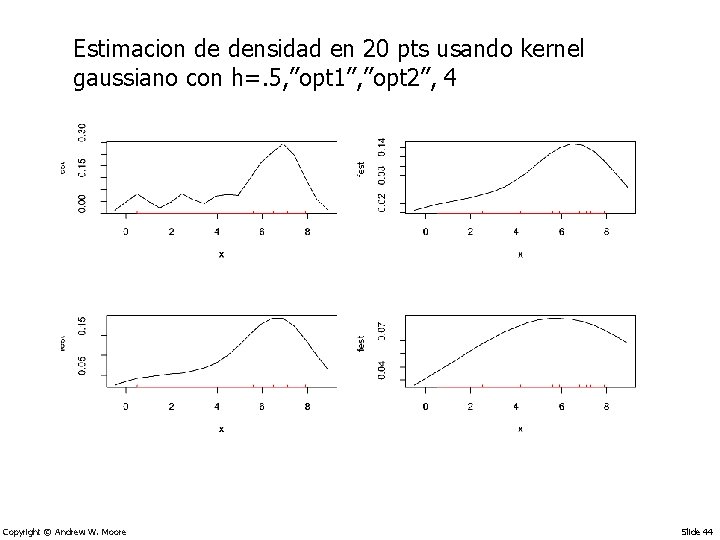
Estimacion de densidad en 20 pts usando kernel gaussiano con h=. 5, ”opt 1”, ”opt 2”, 4 Copyright © Andrew W. Moore Slide 44
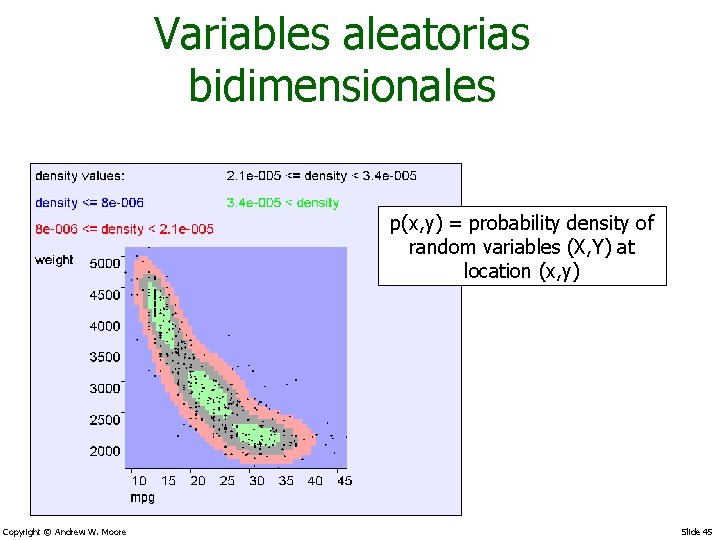
Variables aleatorias bidimensionales p(x, y) = probability density of random variables (X, Y) at location (x, y) Copyright © Andrew W. Moore Slide 45
Estimadores de funcion de densidad bi-dimensionales Histogramas A area de la clase • K-nearest neighbors: Ak es el area ncluyendo hasta el k-esimo vecino • Kernel density estimators • Copyright © Andrew W. Moore Slide 46
Estimacion de kernel bivariado Sean xi=(x, y) los valores observados y t=(t 1, t 2) un punto del plano donde se desea estimar la densidad conjunta Si h 1=h 2=h Copyright © Andrew W. Moore Slide 47
• (a 1, a 2)H-1 donde Copyright © Andrew W. Moore Slide 48
Estimacion de densidad-Kernel Gaussiano bivariado Copyright © Andrew W. Moore Slide 49
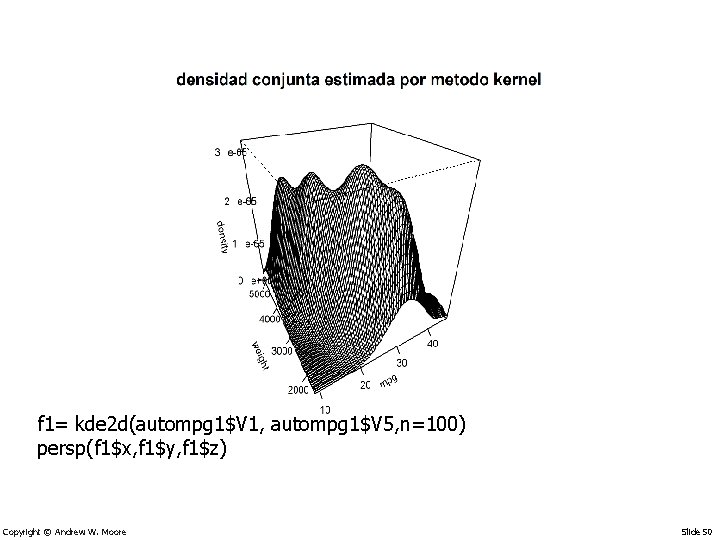
f 1= kde 2 d(autompg 1$V 1, autompg 1$V 5, n=100) persp(f 1$x, f 1$y, f 1$z) Copyright © Andrew W. Moore Slide 50
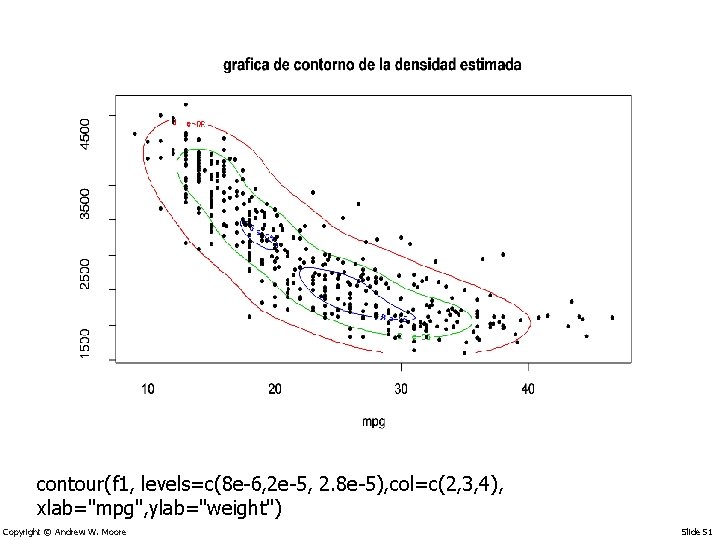
contour(f 1, levels=c(8 e-6, 2 e-5, 2. 8 e-5), col=c(2, 3, 4), xlab="mpg", ylab="weight") Copyright © Andrew W. Moore Slide 51
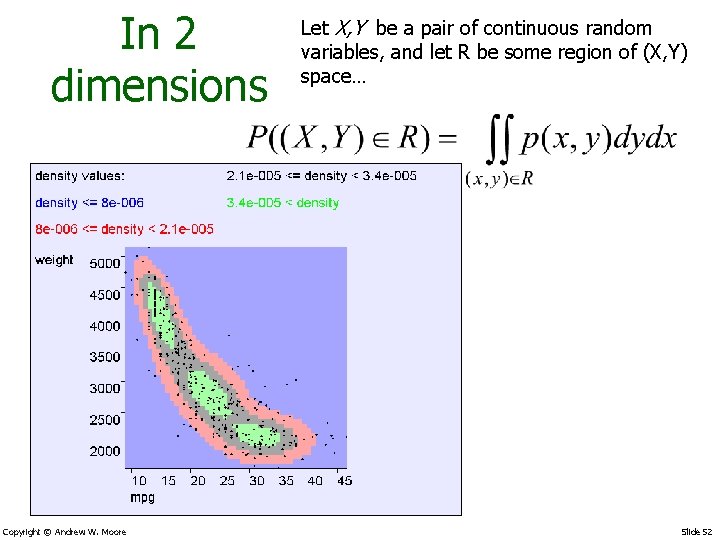
In 2 dimensions Copyright © Andrew W. Moore Let X, Y be a pair of continuous random variables, and let R be some region of (X, Y) space… Slide 52
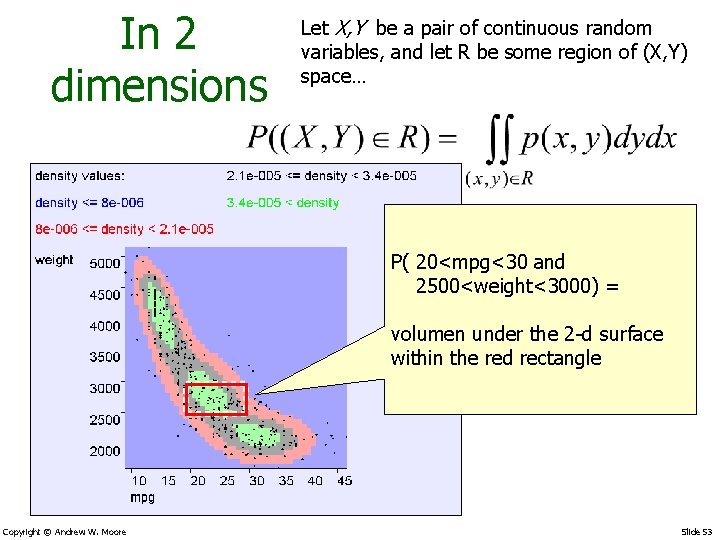
In 2 dimensions Let X, Y be a pair of continuous random variables, and let R be some region of (X, Y) space… P( 20<mpg<30 and 2500<weight<3000) = volumen under the 2 -d surface within the red rectangle Copyright © Andrew W. Moore Slide 53
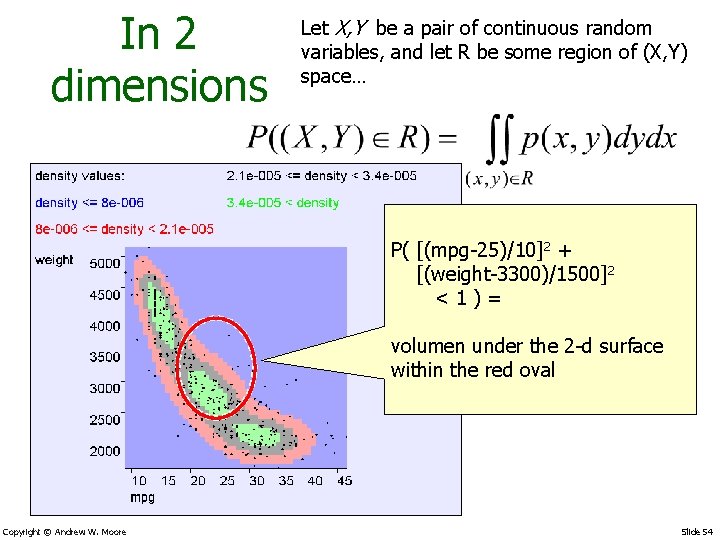
In 2 dimensions Let X, Y be a pair of continuous random variables, and let R be some region of (X, Y) space… P( [(mpg-25)/10]2 + [(weight-3300)/1500]2 < 1 ) = volumen under the 2 -d surface within the red oval Copyright © Andrew W. Moore Slide 54
In 2 dimensions Let X, Y be a pair of continuous random variables, and let R be some region of (X, Y) space… Take the special case of region R = “everywhere”. Remember that with probability 1, (X, Y) will be drawn from “somewhere”. So. . Copyright © Andrew W. Moore Slide 55
In 2 dimensions Copyright © Andrew W. Moore Let X, Y be a pair of continuous random variables, and let R be some region of (X, Y) space… Slide 56
In m dimensions Copyright © Andrew W. Moore Let (X 1, X 2, …Xm) be an n-tuple of continuous random variables, and let R be some region of Rm … Slide 57
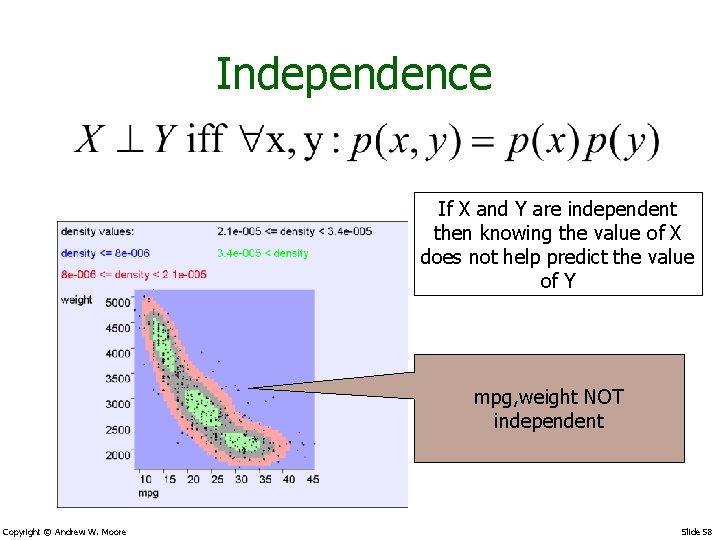
Independence If X and Y are independent then knowing the value of X does not help predict the value of Y mpg, weight NOT independent Copyright © Andrew W. Moore Slide 58
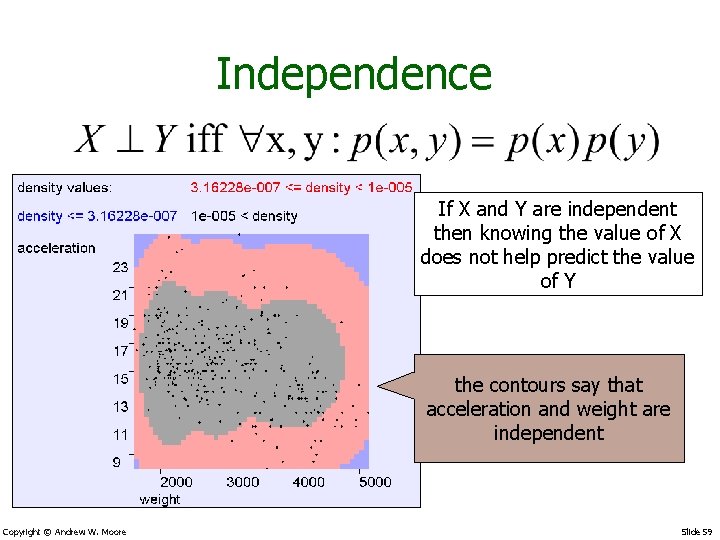
Independence If X and Y are independent then knowing the value of X does not help predict the value of Y the contours say that acceleration and weight are independent Copyright © Andrew W. Moore Slide 59
![Multivariate Expectation E[mpg, weight] = (24. 5, 2600) The centroid of the cloud Copyright](http://slidetodoc.com/presentation_image_h/0be08d797e33b982297acce6e8a8cb6e/image-60.jpg "Multivariate Expectation E[mpg, weight] = (24. 5, 2600) The centroid of the cloud Copyright")
Multivariate Expectation E[mpg, weight] = (24. 5, 2600) The centroid of the cloud Copyright © Andrew W. Moore Slide 60
Multivariate Expectation > f 1= kde 2 d(autompg 1$mpg, autompg 1$weight, n=100) > dx=f 1$x[2]-f 1$x[1] > dy=f 1$y[2]-f 1$y[1] > dx [1] 0. 379798 > dy [1] 35. 62626 > meanmpg=sum(f 1$x*f 1$z)*dx*dy [1] 22. 48855 > meanweight=sum(f 1$y*f 1$z)*dx*dy [1] 2848. 638 >#estimated mean > mean(autompg 1$weight) [1] 2977. 584 > mean(autompg 1$mpg) [1] 23. 44592 Copyright © Andrew W. Moore Slide 61
Multivariate Expectation Copyright © Andrew W. Moore Slide 62
Test your understanding • All the time? Siempre • Only when X and Y are independent? • It can fail even if X and Y are independent? Copyright © Andrew W. Moore Slide 63
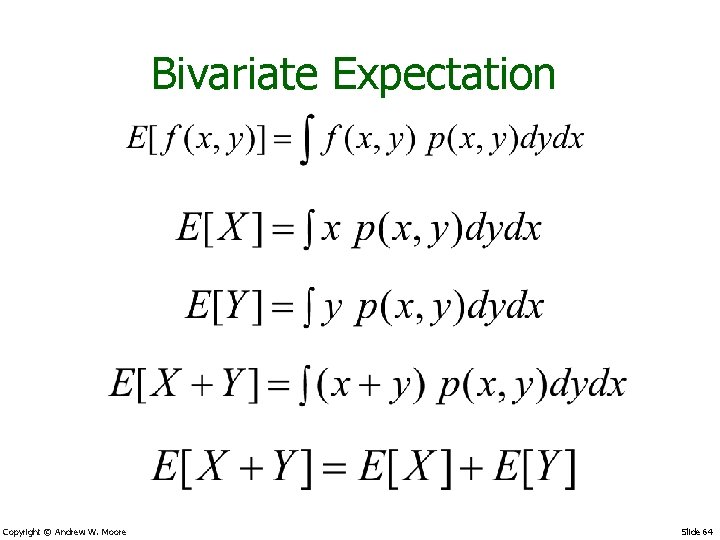
Bivariate Expectation Copyright © Andrew W. Moore Slide 64
Bivariate Covariance Copyright © Andrew W. Moore Slide 65
Bivariate Covariance Copyright © Andrew W. Moore Slide 66
![Covarianza y desviacion estandar estimadas entre mpg y weight > cov(autompg 1[, c(1, 5)])](http://slidetodoc.com/presentation_image_h/0be08d797e33b982297acce6e8a8cb6e/image-67.jpg "Covarianza y desviacion estandar estimadas entre mpg y weight > cov(autompg 1[, c(1, 5)])")
Covarianza y desviacion estandar estimadas entre mpg y weight > cov(autompg 1[, c(1, 5)]) mpg weight mpg 60. 91814 -5517. 441 weight -5517. 44070 721484. 709 > sd(autompg 1$mpg) [1] 7. 805007 > sd(autompg 1$weight) [1] 849. 4026 Copyright © Andrew W. Moore Slide 67
![Covariance Intuition E[mpg, weight] = (24. 5, 2600) Copyright © Andrew W. Moore Slide](http://slidetodoc.com/presentation_image_h/0be08d797e33b982297acce6e8a8cb6e/image-68.jpg "Covariance Intuition E[mpg, weight] = (24. 5, 2600) Copyright © Andrew W. Moore Slide")
Covariance Intuition E[mpg, weight] = (24. 5, 2600) Copyright © Andrew W. Moore Slide 68
![Covariance Intuition Principal Eigenvector of S E[mpg, weight] = (24. 5, 2600) Copyright ©](http://slidetodoc.com/presentation_image_h/0be08d797e33b982297acce6e8a8cb6e/image-69.jpg "Covariance Intuition Principal Eigenvector of S E[mpg, weight] = (24. 5, 2600) Copyright ©")
Covariance Intuition Principal Eigenvector of S E[mpg, weight] = (24. 5, 2600) Copyright © Andrew W. Moore Slide 69
Regression Line Notice that the regression line pass trough ( x, y) Copyright © Andrew W. Moore Slide 70
Regression Line >l 1=lm(weight~mpg, data=autompg 1) > l 1 Call: lm(formula = weight ~ mpg, data = autompg 1) Coefficients: (Intercept) mpg 5101. 11 -90. 57 >#slope of regression line >slope= -5517. 44/60. 918 [1] -90. 571 Copyright © Andrew W. Moore Slide 71
![Primer Principal component > a=cov(autompg 1[, c(1, 5)]) > eigen(a) $values [1] 721526. 90386](http://slidetodoc.com/presentation_image_h/0be08d797e33b982297acce6e8a8cb6e/image-72.jpg "Primer Principal component > a=cov(autompg 1[, c(1, 5)]) > eigen(a) $values [1] 721526. 90386")
Primer Principal component > a=cov(autompg 1[, c(1, 5)]) > eigen(a) $values [1] 721526. 90386 18. 72329 $vectors [, 1] [, 2] [1, ] -0. 007647317 0. 999970759 [2, ] 0. 999970759 0. 007647317 #slope of primer principal component >. 99997/-. 00764 [1] – 130. 8861 Copyright © Andrew W. Moore Slide 72
Covariance Fun Facts • True or False: If sxy = 0 then X and Y are independent. False • True or False: If X and Y are independent then sxy = 0. True • True or False: If sxy = sx sy then X and Y are deterministically related. True How could you prove or disprove these? • True or False: If X and Y are deterministically related then sxy = sx sy. false Copyright © Andrew W. Moore Slide 73
Test your understanding • All the time? • Only when X and Y are independent? Cierto • It can fail even if X and Y are independent? Copyright © Andrew W. Moore Slide 74
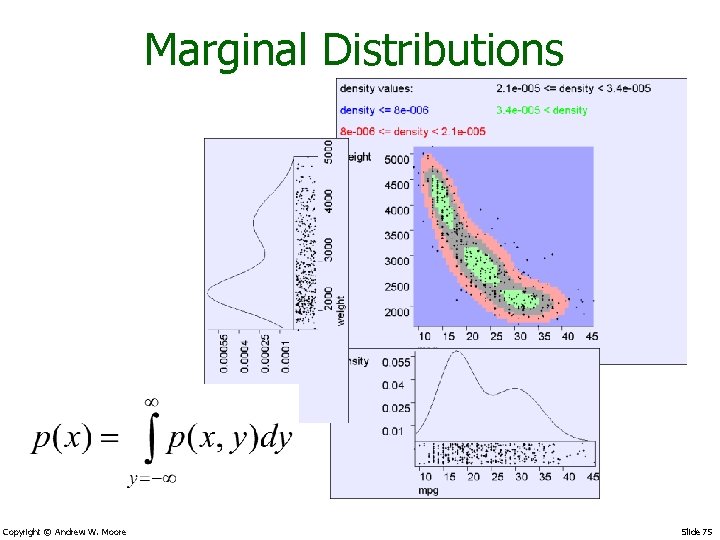
Marginal Distributions Copyright © Andrew W. Moore Slide 75
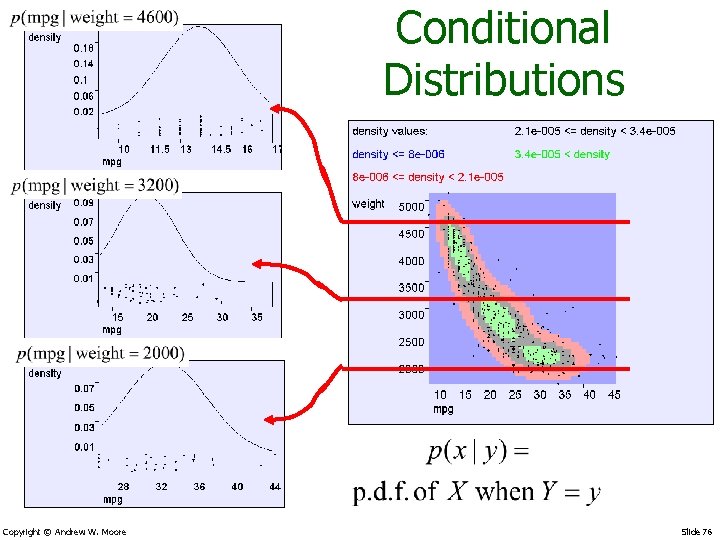
Conditional Distributions Copyright © Andrew W. Moore Slide 76
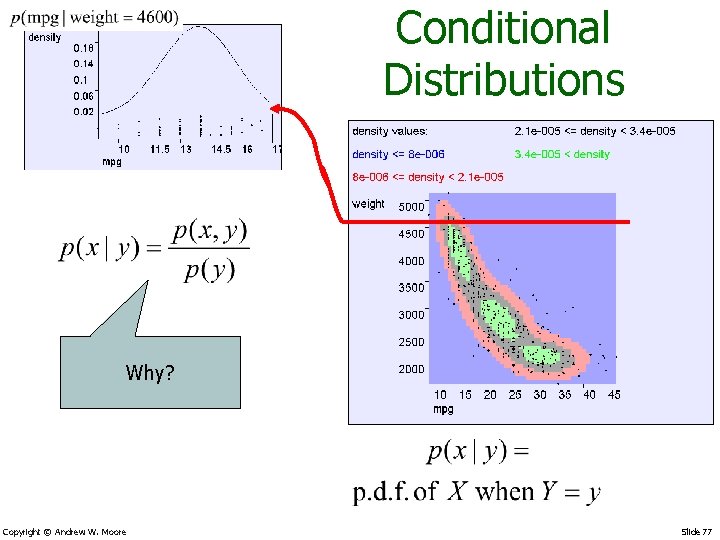
Conditional Distributions Why? Copyright © Andrew W. Moore Slide 77
Independence Revisited It’s easy to prove that these statements are equivalent… Copyright © Andrew W. Moore Slide 78
More useful stuff (These can all be proved from definitions on previous slides) Bayes Rule Copyright © Andrew W. Moore Slide 79
Mixing discrete and continuous variables Bayes Rule Copyright © Andrew W. Moore Slide 80
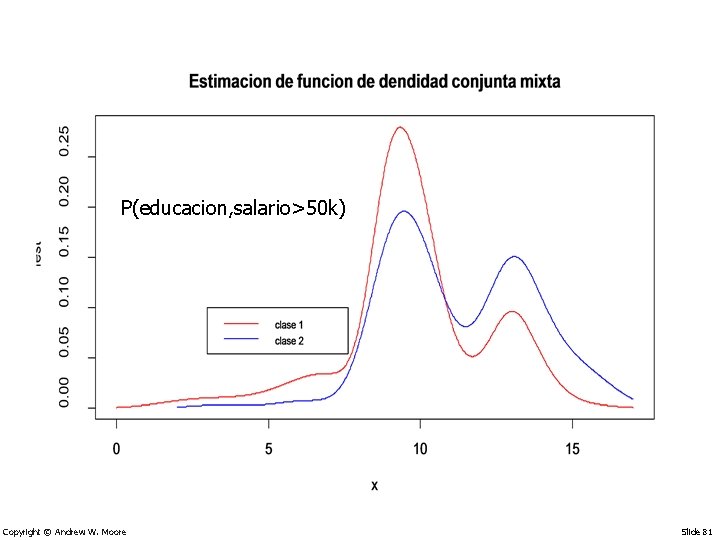
P(educacion, salario>50 k) Copyright © Andrew W. Moore Slide 81
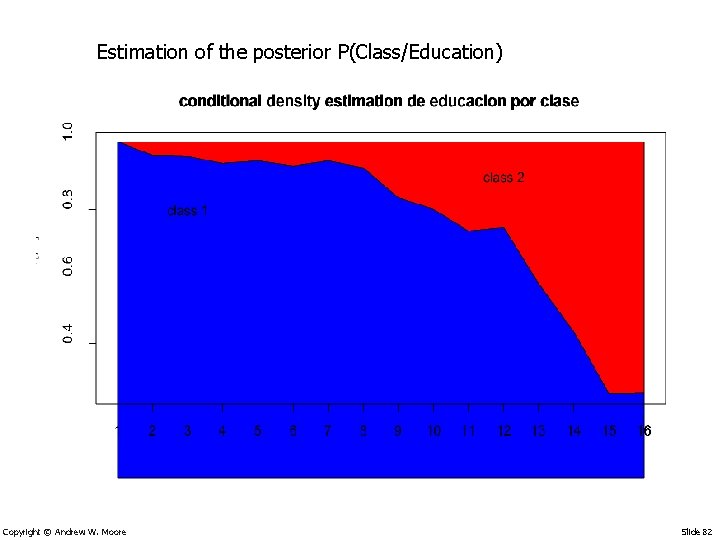
Estimation of the posterior P(Class/Education) Copyright © Andrew W. Moore Slide 82
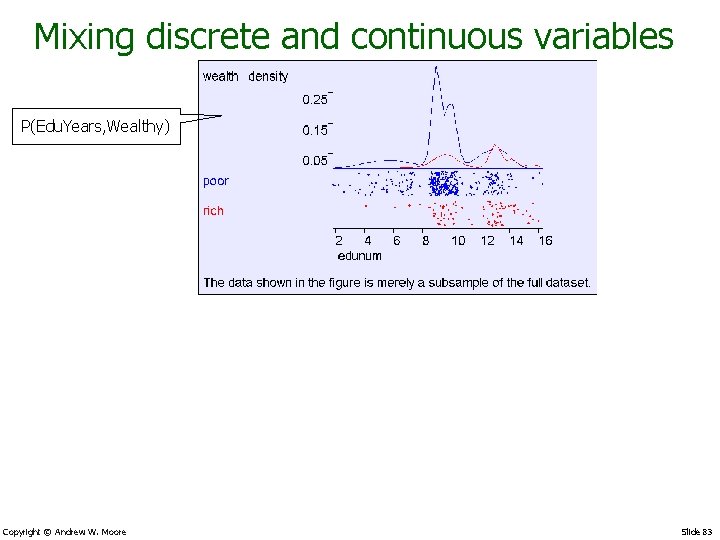
Mixing discrete and continuous variables P(Edu. Years, Wealthy) Copyright © Andrew W. Moore Slide 83
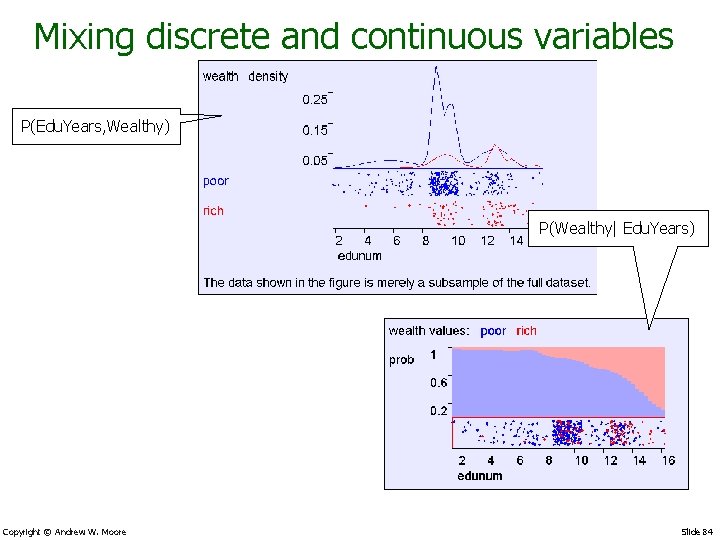
Mixing discrete and continuous variables P(Edu. Years, Wealthy) P(Wealthy| Edu. Years) Copyright © Andrew W. Moore Slide 84
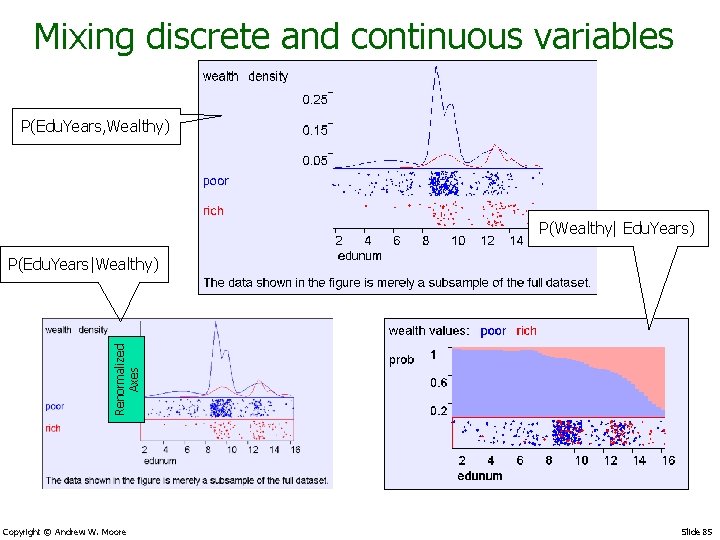
Mixing discrete and continuous variables P(Edu. Years, Wealthy) P(Wealthy| Edu. Years) Renormalized Axes P(Edu. Years|Wealthy) Copyright © Andrew W. Moore Slide 85
Ejercicios • Suppose X and Y are independent realvalued random variables distributed between 0 and 1: • What is p[min(X, Y)]? • What is E[min(X, Y)]? • Prove that E[X] is the value u that minimizes E[(X-u)2] • What is the value u that minimizes E[|X-u|]? Copyright © Andrew W. Moore Slide 86
- Slides: 86