Probability contd 1 Objectives To construct and understand

Probability cont’d… 1

Objectives Ø Ø Ø To construct and understand a contingency/crosstabulation table To understand that compound events involve the occurrence of more than one event To describe and compute a conditional probability To understand be able to utilize the complement rule To compute the probabilities of compound events using the addition and the multiplication rules 2

Bivariate Data n n The values of two different variables that are obtained from the same population element Each of the two variables may be either qualitative or quantitative 3

Cross-tabulation or Contigency table n When bivariate data result from two qualitative (attribute or categorical) variables, the data are often arranged on a cross-tabulation or contingency table. 4

Example. K n n Thirty students from RTU-CEIT were randomly identified and classified according to two variables: gender (M/F) and major (CE, EE) as shown in the table (next slide). These 30 bivariate data can be summarized on a 2 x 3 cross-tabulation table, where the two rows represent the two genders, male and female, and the three columns represent the three major categories of CE, ECE and EE. 5

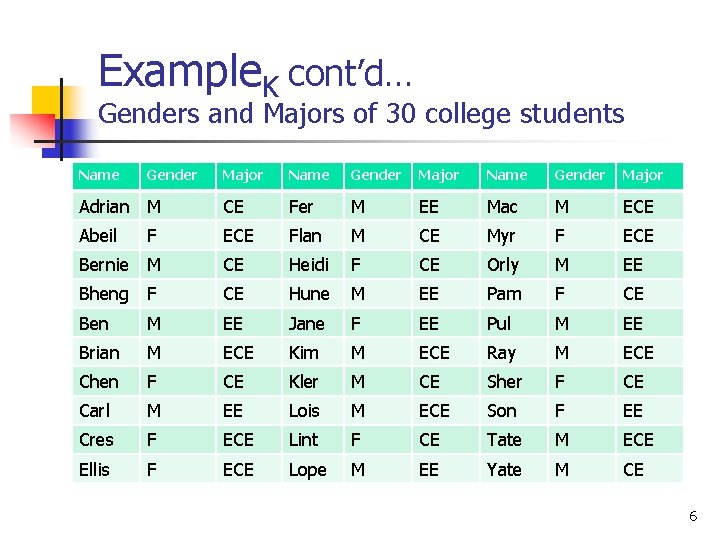
Example. K cont’d… Genders and Majors of 30 college students Name Gender Major Adrian M CE Fer M EE Mac M ECE Abeil ECE Flan M CE Myr F ECE Bernie M CE Heidi F CE Orly M EE Bheng F CE Hune M EE Pam F CE Ben M EE Jane F EE Pul M EE Brian M ECE Kim M ECE Ray M ECE Chen F CE Kler M CE Sher F CE Carl M EE Lois M ECE Son F EE Cres F ECE Lint F CE Tate M ECE Ellis F ECE Lope M EE Yate M CE F 6

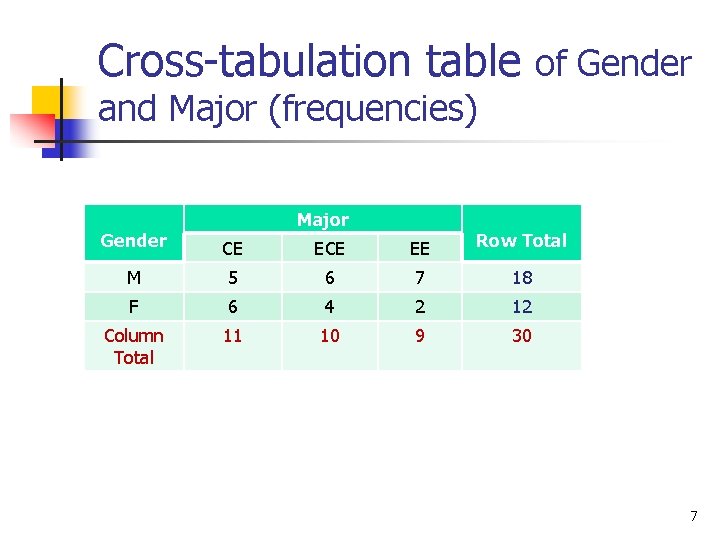
Cross-tabulation table of Gender and Major (frequencies) Major Gender CE EE Row Total M 5 6 7 18 F 6 4 2 12 Column Total 11 10 9 30 7

n The resulting 2 x 3 cross-tabulation (contingency) table shows the frequency for each cross-category of the two variables along with the row and column totals, called marginal totals or marginals. The total of the marginal totals is the grand total and is equal to n, the sample size. 8

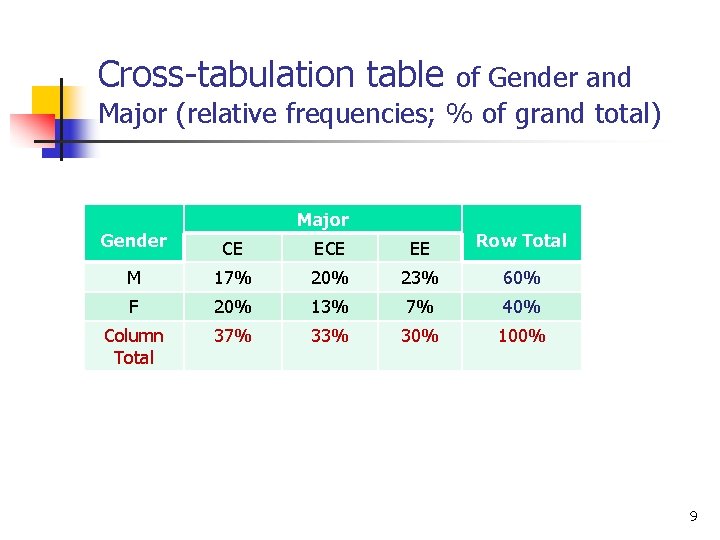
Cross-tabulation table of Gender and Major (relative frequencies; % of grand total) Major Gender CE EE Row Total M 17% 20% 23% 60% F 20% 13% 7% 40% Column Total 37% 33% 30% 100% 9

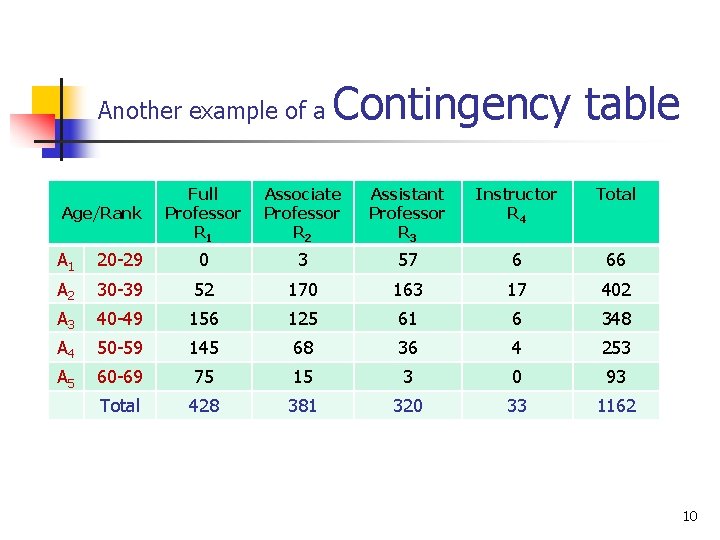
Another example of a Age/Rank Contingency table Full Professor R 1 Associate Professor R 2 Assistant Professor R 3 Instructor R 4 Total A 1 20 -29 0 3 57 6 66 A 2 30 -39 52 170 163 17 402 A 3 40 -49 156 125 61 6 348 A 4 50 -59 145 68 36 4 253 A 5 60 -69 75 15 3 0 93 Total 428 381 320 33 1162 10

Rules of Probability n n Often, one wants to know the probability of a compound event and the only data available are the probabilities of the related simple events. Compound events n Combinations of more than one simple event 11

Finding the n Complementary events n n n Probability of “Not A” Complement of an event A, : The set of all sample points (simple events) in the sample space that do not belong to the event A read as “A complement” 12

Examples of complementary events Event A Complement of event A, success failure selected voter is a Filipino selected voter is not a Filipino no heads on 10 tosses at least one head 13

Complement Rule n n Probability of A complement = one – probability of A Or P( ) = 1 – P(A) 14

Example n n Two dice are rolled. What is the probability that the sum is at least 3 (that is, 3, 4, 5, …, 12)? P(sum is at least 3) = P( ) = 1 – P(A) n n P(sum of 2) = P(A) = 1/36 Therefore (“less than 3” and “at least 3” are complementary events) n P(sum is at least 3) = P( ) n = 1 – 1/36 = 35/36 15

Finding the n Probability of “A or B” An hourly wage earner wants to estimate the chances of “receiving a promotion or getting a pay raise. ” The worker would be happy with either outcome. 16

Addition Rule. NMEE n n n Let A and B be two events in a sample space, S Probability of A or B = probability of A + probability of B - probability of A and B Or P(A or B) = P(A) + P(B) – P(A and B) 17

Addition Rule. MEE n n n Let A and B be two events in a sample space, S Probability of A or B = probability of A + probability of B n n Or P(A or B) = P(A) + P(B) n because P(A and B) = 0 18

Example From the data (see next slide), find the probability that a faculty selected is an associate professor or in his 40’s. n Solution: n Let R 2 = event that the faculty selected is an associate professor n A 3 = event that the faculty selected is in his 40’s 19

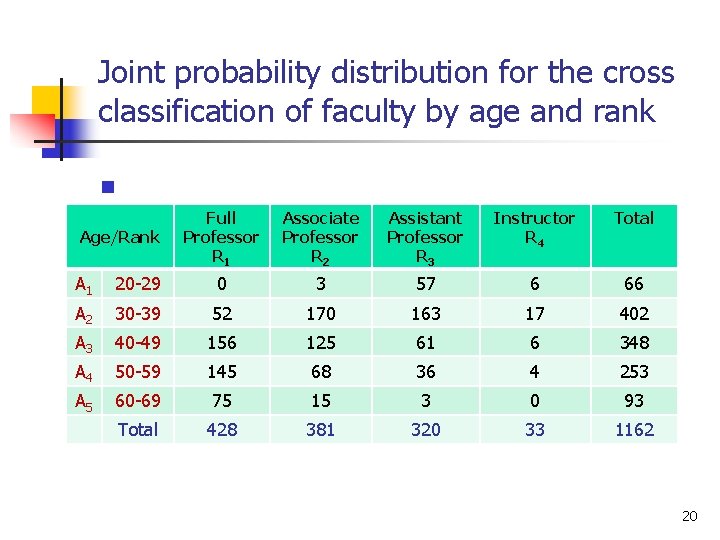
Joint probability distribution for the cross classification of faculty by age and rank n Age/Rank Full Professor R 1 Associate Professor R 2 Assistant Professor R 3 Instructor R 4 Total A 1 20 -29 0 3 57 6 66 A 2 30 -39 52 170 163 17 402 A 3 40 -49 156 125 61 6 348 A 4 50 -59 145 68 36 4 253 A 5 60 -69 75 15 3 0 93 Total 428 381 320 33 1162 20

Solution n cont’d… R 2 and A 3 = events that the faculty selected is an associate professor in his 40’s P(R 2 or A 3) = 0. 329 + 0. 299 – 0. 108 = 0. 520 21

Another solution n Refer to the contigency table, page 13 R 2 = 381 A 3 = 348 22

Example. M n The table (next slide) is a contingency table that shows 500 TV sets classified by screen size and whether each set is colored or not. What is the probability that a set selected at random will be either a colored set or have a screen size of less than 21 inches. 23

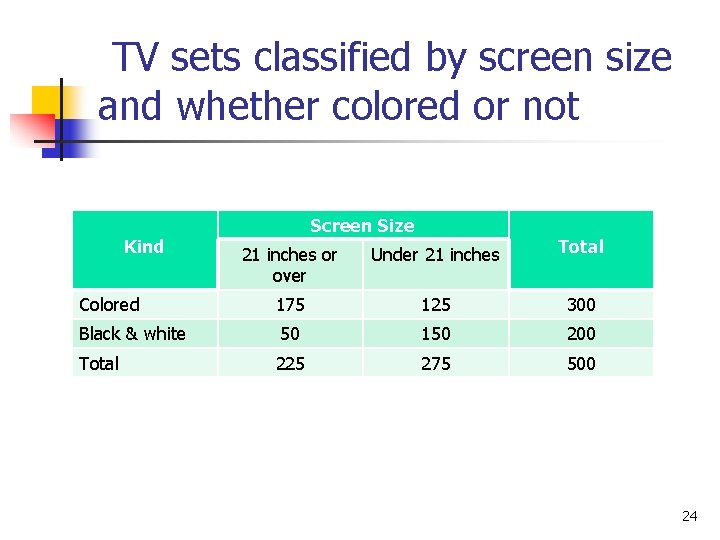
TV sets classified by screen size and whether colored or not Kind Screen Size 21 inches or over Under 21 inches Total Colored 175 125 300 Black & white 50 150 200 Total 225 275 500 24

Solution n Events of interest: n n n A: a colored TV is selected B: a set with screen size of less that 21 inches is selected P(A) = 300/500 = 0. 60 P(B) = 275/500 = 0. 55 P(A&B) = 125/500 = 0. 25 P(A or B) = 0. 60 + 0. 55 – 0. 25 = 0. 90 25

Finding the n n Probability of “A and B” Suppose a criminal justice professor wants his class to determine the likeliness of the event “a driver is ticketed for a speeding violation and the driver had previously attended a defensive driving class. ” The students are confident they can find the probabilities of “a driver being ticketed for speeding” and “a driver has attended a defensive driving class separately. 26

Conditional Probability of Events n n the relative frequency with which an event can be expected to occur under the condition that additional preexisting information is known about some other event. P(A│B) symbolyzes n The probability of event A occurring under the condition that event B is known to already exist 27

Ways to say or express the conditional probability, P(A│B) n n n The “probability of A, given B. ” The “probability of A, knowing B. ” The “probability of A happening, knowing B has already occurred. ” 28

Example. K n The data from a National Election exit poll of 13, 660 voters in 250 precincts across the country on May, 2004, are shown in the table (see next slide). 29

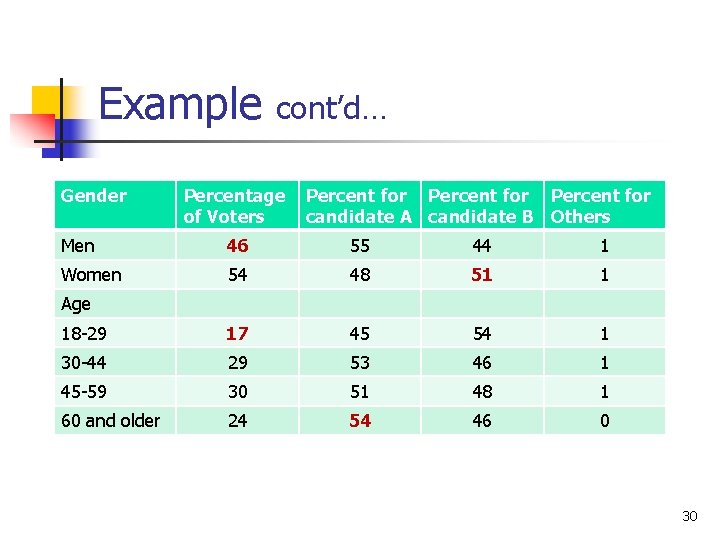
Example Gender cont’d… Percentage of Voters Percent for candidate A candidate B Others Men 46 55 44 1 Women 54 48 51 1 18 -29 17 45 54 1 30 -44 29 53 46 1 45 -59 30 51 48 1 60 and older 24 54 46 0 Age 30

Example. K n cont’d… One person is to be selected at random from the sample of 13, 600 voters. Using the table, find the answers to the following probability questions (see next slide). 31

Example. K n n cont’d… 1. What is the probability the person selected is a man? 2. What is the probability the person selected is from age 18 to 29? 3. Knowing the voter selected was a woman, what is the probability she voted for candidate B? 4. What is the probability the person selected voted for candidate A if the voter was 60 or older? 32

Solution n n n 1. P(voter selected is a man) = 0. 46 2. P(voter selected is of age 18 to 29) = 0. 17 3. P(candidate B│woman) = 0. 51 4. P(candidate A│60 and older) = 0. 54 Note: The first two are simple probabilities, whereas the last two are conditional probabilities. 33

Example. K n The data from a nationwide exit poll of 1000 voters in 25 precincts across the country on May, 2004, are shown in the table (see next slide). 34

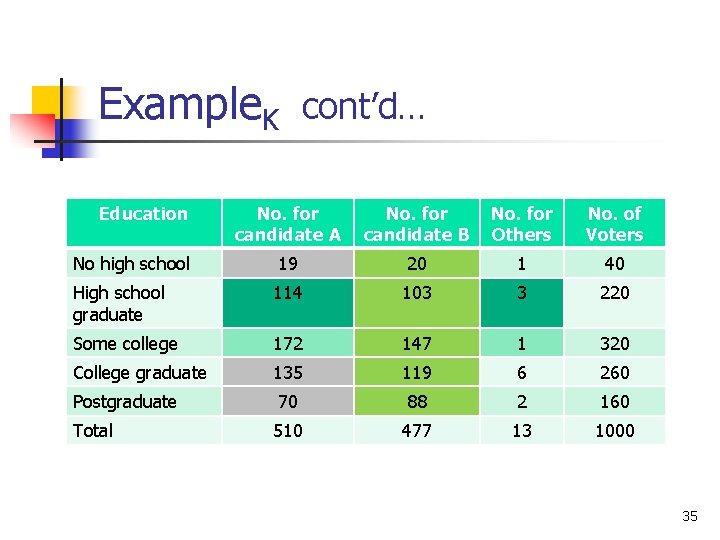
Example. K cont’d… Education No. for candidate A No. for candidate B No. for Others No. of Voters No high school 19 20 1 40 High school graduate 114 103 3 220 Some college 172 147 1 320 College graduate 135 119 6 260 Postgraduate 70 88 2 160 Total 510 477 13 1000 35

Example. K cont’d… n n One person is to be selected at random from the preceding sample of 1000 voters. Using the table, find the answer to the following probability questions (next slide): 36

Example. K cont’d… n n 1. Knowing the voter selected was a high school graduate, what is the probability the person voted for candidate B? 2. Knowing the voter selected had some college education, what is the probability the person voted for candidate A? 37

Example. K cont’d… n n 3. Knowing the selected person voted for candidate B, what is the probability the voter has a postgraduate education? 4. Knowing the selected person voted for candidate A, what is the probability the voter does not have a high school education? 38

Solution n n 1. P(candidate B│high school graduate) = 103/220 = 0. 46818 = 0. 47 2. P(candidate A│some college) = 172/320 = 0. 5375 = 0. 54 3. P(post graduate│candidate B) = 88/477 = 0. 1844 = 0. 18 4. P(no high school│candidate A) = 19/510 = 0. 0372 = 0. 04 39

Note n When finding a conditional probability, some outcomes from the list of possible outcomes will be eliminated as possibilities as soon as the condition is known. Consider question 4. As soon as the conditional stated “knowing the selected person voted for candidate A, ” the 477 who voted for candidate B and the 13 voting for Others were eliminated, leaving the 510 possible outcomes. 40

Independent Events n n Two events are independent if the occurrence (or nonoccurrence) of one gives us no information about the likeliness of occurrence for the other. Or n n The probability of A remains unchanged after we know that B has happened (or has not happened) P(A) = P(A│B) = P(A│not B) 41

Dependent Events n Events that are not independent. That is, the occurrence of one event does have an effect on the probability for occurrence of the other event. 42

OR n Two events A and B are said to be independent if and only if either P(A│B) = P(A) P(B│A) = P(B) n Otherwise n n n the events are said to be dependent 43

Multiplication Rule. IE n n Let A and B be two events defined in sample space, S Probability of A and B = Probability of A x probability of B When two events are involved, either event can be identified as A, with the other identified as B. n P(A and B) = P(A). P(B) 44

Multiplication Rule. DE n n Let A and B be two events defined in sample space, S Probability of A and B = Probability of A x probability of B, knowing A When two events are involved, either event can be identified as A, with the other identified as B. P(A and B) = P(A). P(B│A) Or P(B and A) = P(B). P(A│B) n 45

Conditional probability of A, given that B has occurred 46

Conditional probability of B, given that A has occurred 47

Example. M n n Using the data and events A and B as defined in the table on page 18, compute P(A│B) and P(B│A). Solution: 48

Example. M n There are 10 balls in a container, 3 of which are red and dotted, 1 is red and striped, 2 are gray and dotted and 4 are gray and striped. Calculate the following probabilities: (a) probability of red given dotted, (b) probability of red given striped, © probability of gray given dotted, (d) probability of gray given striped, and (e) probability of red and dotted (joint probability) 49

Solution n a. Probability of red given dotted 50

Solution cont’d… n b. Probability of red given striped 51

Solution cont’d… n c. Probability of gray given dotted 52

Solution cont’d… n d. Probability of gray given striped 53

Solution cont’d… n n n e. Probability of red and dotted (joint probability) P(R and D) = P(red and dotted) = P(R│D) P(D) = 0. 6 (5/10) = 0. 30 54

Example. B n n Two cards are drawn from a deck of 52 cards. Calculate the probability that the draw includes an ace and a ten. Solution: n Events of interest A: Draw an ace and a ten B: Draw the ace on the first draw and the ten on the second C: Draw the ten on the first and the ace on the second 55

Solution n n n B = B 1 and B 2 C = C 1 and C 2 where B 1: Draw an ace on the first draw B 2: Draw a ten on the second draw C 1: Draw a ten on the first draw C 2: Draw an ace on the second draw 56

Solution cont’d… n Applying the Multiplicative Rule: 57

Solution cont’d… n n Applying the Additive Rule: P(A) = P(B) + P© 58

Example. M n Two cards are drawn from a deck of 52 cards. Calculate the probability that the draw includes a Jack and a Queen. 59

Solution. M n Consider the events of interest (see table below): Event First draw Second draw B Jack: P(J) = 4/52 Queen: P(Q) = 4/51 C Queen: P(Q) = 4/52 Jack: P(J) = 4/51 60

Solution n a. Draw a Jack and a Queen. Find P(J&Q) and P(Q&J). b. Draw the Jack on the first draw and a Queen on the second draw. Find P(J) then P(Q). c. Draw a Queen on the first draw and a Jack on the second draw. Find P(Q) then P(J). 61

Solution cont’d… n In event B: n n n P(B) = P(J&Q) = P(J) P(Q) Since J & Q are independent P(B) =P(J&Q) = (4/52)(4/51) = 4/663 62

Solution cont’d… n In event C: n n n P© = P(Q&J) = P(Q) P(J) P© = (4/52)(4/51) = 4/663 P(A) = P(B) + P© = 4/664 + 4/663 = 8/663 = 0. 012 63