Probability Concepts Introduction to Business Statistics 5 e

Events and Probability • An activity for which the outcome is uncertain is an experiment. • An event consists of one more possible outcomes of the experiment. Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Relative Frequency Approach Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Datacomp Survey Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing M = a male is selected F = a female is selected U = the person selected is under 30 B = the person selected is between 30 and 45 O = the person selected is over 45

Marginal Probability the probability of a single event used to define the contingency table. P(M) = 120/200 =. 6 P(U) =. 5 Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing P(B) =. 25 P(F) = 80/200 =. 4 P(O) =. 25

Complement of an Event The Complement of an event A is the event that A does not occur. P(A) + P( ) = 1 P(M) = 1 - P(M) =. 4 Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Joint Probability • The probability of the occurrence of two events at the same time. The probability of selecting a person who is a female and under 30 P(F and U) = 40/200 =. 2 Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Union of Events The Union of events is the probability of either event A or event B occurring. The probability of selecting a person who is Male or under 30. P(M or U) = (120 + 40) / 200 =. 8 Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Conditional Probability Whenever you are given information and are asked to find a probability based on this information, the result is a Conditional probability. P(A|B) Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Independent Events If the P(A) = P(A|B) then event A is said to be independent of event B. P(M) = P(M|U) =. 6 Thus event M is independent of event U. Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Mutually Exclusive Events If an event can not occur when another event has occurred the two events are said to be Mutually Exclusive. Selecting a Male and a Female are mutually exclusive events. Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing P(M|F) = 0

Additive Probability Rules General Additive Rule • P(A or B) = P(A) + P(B) - P(A and B) Special Additive Rule • If A and B are mutually exclusive then: P(A or B) = P(A) + P(B) Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Conditional Probability Rules General Conditional Probability Rule P(A|B) = P(A and B) P(B) 0 P(B) Special Conditional Probability Rule If A and B are independent then: P(A|B) = P(A) P(A and B) = P(A) P(B) Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Tree Diagrams The probability of the event on the right side (say, event B) of the tree is equal to the sum of the paths; that is, all probabilities along a path leading to event B are multiplied, and then summed over all paths leading to B. Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

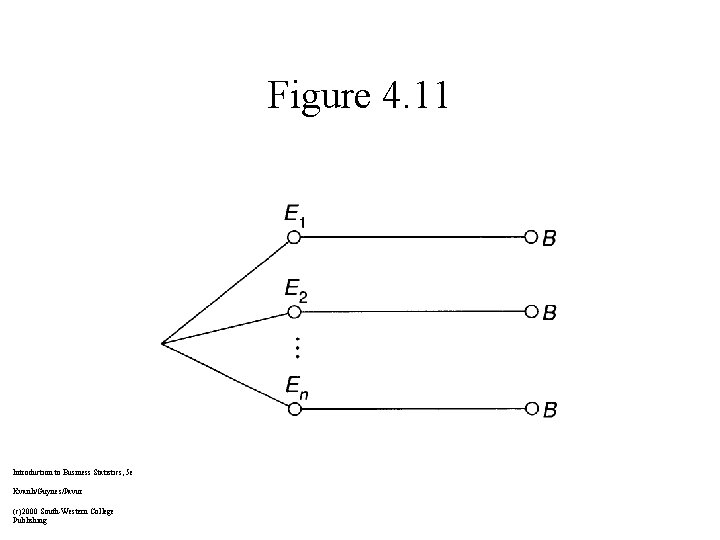
Figure 4. 11 Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Counting Rules • Counting Rules determine the number of outcomes that exist for a certain broad range of experiments. • Filling Slots • Permutations • Combinations Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Filling Slots • Use counting rule 1 to fill k different slots. Let: n 1 = the number of ways to filling the first slot n 2 = the number of ways to filling the second slot after the first slot is filled nk = the number of ways to filling the kth slot after slots 1 though k - 1 The number of ways of filling all k slots is: n 1 n 2 n 3 … nk Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Permutations is the counting situation in which you select people without replacement and where order of selection is important. Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing

Combinations is the counting situation in which you select people without replacement and where order of selection is not important. Introduction to Business Statistics, 5 e Kvanli/Guynes/Pavur (c)2000 South-Western College Publishing