Probability Chance Lesson 4 Introduction In todays lesson

Probability (Chance) Lesson 4

Introduction In today’s lesson, we will be using our knowledge of both probability and statistics from the previous unit to conduct an investigation on whether it is more likely to roll a 6 when you whisper to the dice than if you roll the dice silently. You will make predictions, record results in a tally, display your results in a graph, discuss your findings and then complete a reflection activity. This will further develop your understanding for higher and lower probability of certain events occurring, while engaging in a fun, enjoyable activity!

Probability Power. Point questions 1 - 7

Recap of previous lessons Probability is the likelihood of an event to occur. Probability is defined as a number between 0 and 1. Probability is represented as a fraction, a decimal or a percentage. Draw a probability number line on the board: How likely is it that an AFL player will still play AFL at the age of 50? What is the probability of flipping a coin and getting ‘heads’? What is the chance that I will play cricket tonight? What is the likelihood that the Adelaide Crows will get smashed again next week? What is the probability of me selecting a red smartie from a bag of smarties? Use the probability formula: Pr (red) = (“The probability of a red smartie occurring is ___”) I have 12 smarties in total 3 are blue 3 are orange 4 are red 2 are green

Rolling a 6 Investigation In pairs, you will complete the dice investigation ‘Roll Me A 6!’ You will: Predict what you think will happen during the experiment. Record your ideas on the Making Predictions Worksheet. Conduct the experiment. Roll a dice 20 times, whispering Roll me a six! before each roll. Record what happens each time in the table provided on the Conducting the Experiment Worksheet. Then roll the dice 20 more times, without whispering. Record what happens each time in the second table. Use the Recording Results Worksheet to show the frequency that each number was rolled during each part of the experiment as a number, as a fraction, as a decimal and as a percentage. Draw a side-by-side column graph on the Displaying Results Worksheet to display the results of each part of the experiment. Answer the questions on the Discussion and Conclusion Worksheet to compare the results of the experiment with your prediction.

Explicit Teaching – model on whiteboard Making predictions – “I predict the number 4 will occur the most frequently when I roll the dice 20 times. ” Conducting the experiment – *roll the dice – if a 3 occurs, write down ‘ 3’ Recording results – use a tally to record how frequently each number occurred (was rolled) Displaying results – use a column graph to display your data Discussion and conclusion – how did the results compare to your prediction? Reflection – What did you learn from this investigation?

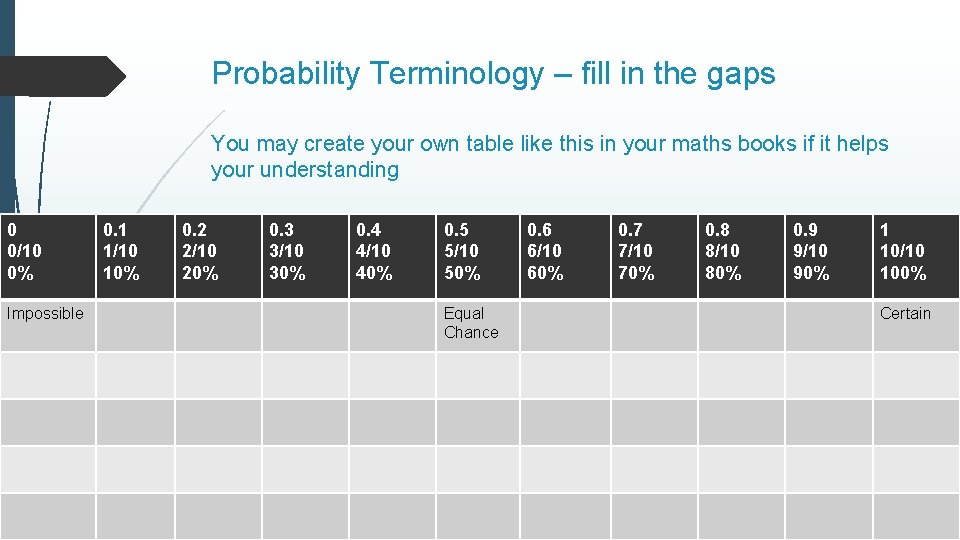
Probability Terminology – fill in the gaps You may create your own table like this in your maths books if it helps your understanding 0 0/10 0% Impossible 0. 1 1/10 10% 0. 2 2/10 20% 0. 3 3/10 30% 0. 4 4/10 40% 0. 5 5/10 50% Equal Chance 0. 6 6/10 60% 0. 7 7/10 70% 0. 8 8/10 80% 0. 9 9/10 90% 1 10/10 100% Certain

Probability Number Line Poster – model on 0 whiteboard 1 In groups of 2 or 3: Create a probability number line poster using large paper! Ensure your number line has all of the relevant words and probability numbers (i. e. impossible = 0, equal chance = 0. 5 or ½ or 50%, certain = 1). Write probability statements directly onto the probability line in the correct area (i. e. “The sun will come up tomorrow. ” is certain). Draw and colour in pictures relating to your event to decorate your poster (i. e. the probability of rolling a six with a dice is… - the picture could be of a dice with the number 6 showing). Make sure your probability poster looks great! You may include definitions for words you are not sure of on your poster (similar to a mini word wall!).