Probability Basics Laws of Probability Odds and Probability
Probability Basics • Laws of Probability • Odds and Probability • Probability Trees

Warm-up • Your friend is tossing a fair coin and obtains 5 heads in a row. • After the 5 th head she proclaims “I’m really due for a tail on the next toss. ” • Explain why this thinking is incorrect.

Warm-up (2) • Non-existent “Law of Averages” – She is not “due” for a tail just because she has 5 heads in a row. (short-run behavior) • Law of Large Numbers – As we repeat a random process over and over, the proportion of times that an event occurs settles down to one number. We call this number the probability. (long-run behavior is a long time! Infinite)

Birthday Problem • What is the smallest number of people you need in a group so that the probability of 2 or more people having the same birthday is greater than 1/2? • Answer: 23 No. of people 23 30 40 60 Probability. 507. 706. 891. 994

Probability • Formal study of uncertainty • The engine that drives Statistics • Primary objectives of Chapters 13, 14: 1. use the rules of probability to calculate appropriate measures of uncertainty. 2. Learn the probability basics so that we can do Statistical Inference

Probability Considerations • Your favorite basketball team has the ball and trails by 2 points with little time remaining in the game. Should your team attempt a gametying 2 -pointer or go for a buzzer-beating 3 -pointer to win the game? (This situation has often been used in Microsoft job interviews). • After a touchdown should a coach kick the extra point or go for two? • The traffic light at Western Blvd/Gorman St is set to be green for Western Blvd 65% of the time. The light has been red the previous 7 times you drove through that intersection on Western Blvd. Today you are “due” for a green light. • On 4 th down should your favorite football team punt or try for the first down?
Randomness and probability Randomness ≠ chaos A phenomenon is random if individual outcomes are uncertain, but there is nonetheless a regular distribution of outcomes in a large number of repetitions.
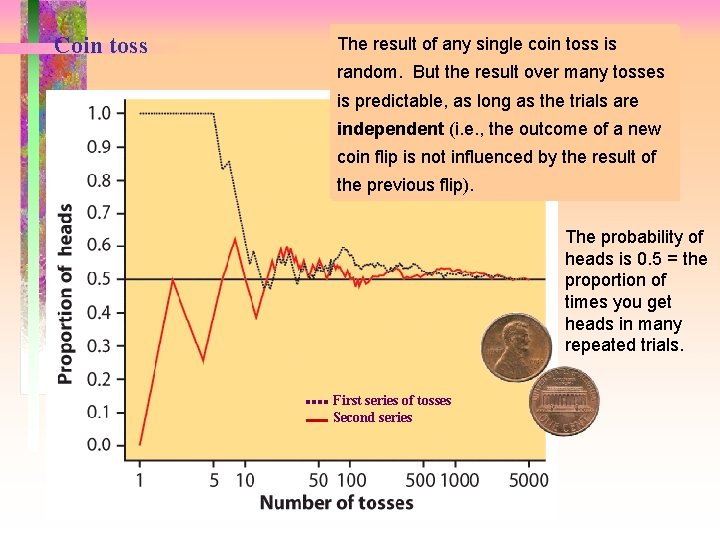
Coin toss The result of any single coin toss is random. But the result over many tosses is predictable, as long as the trials are independent (i. e. , the outcome of a new coin flip is not influenced by the result of the previous flip). The probability of heads is 0. 5 = the proportion of times you get heads in many repeated trials. First series of tosses Second series

Approaches to Probability 1. Relative frequency event probability = x/n, where x=# of occurrences of event of interest, n=total # of observations – Coin, die tossing; nuclear power plants? • Limitations repeated observations not practical

Approaches to Probability - 2 2. Subjective probability individual assigns prob. based on personal experience, anecdotal evidence, etc. 3. Classical approach every possible outcome has equal probability (more later)

Basic Definitions • Experiment: act or process that leads to a single outcome that cannot be predicted with certainty • Examples: 1. Toss a coin 2. Draw 1 card from a standard deck of cards 3. Arrival time of flight from Atlanta to RDU

Basic Definitions - 2 • Sample space: all possible outcomes of an experiment. Denoted by S • Event: any subset of the sample space S; typically denoted A, B, C, etc. Null event: the empty set F Certain event: S

Examples 1. Toss a coin once S = {H, T}; A = {H}, B = {T} 2. Toss a die once; count dots on upper face S = {1, 2, 3, 4, 5, 6} A=even # of dots on upper face={2, 4, 6} B=3 or fewer dots on upper face={1, 2, 3} 3. Select 1 card from a deck of 52 cards. S = {all 52 cards}

Laws of Probability

Laws of Probability - 2 Coin Toss Example: S = {Head, Tail} Probability of heads = 0. 5 Probability of tails = 0. 5 3) The complement of any event A is the event that A does not occur, written as A. The complement rule states that the probability of an event not occurring is 1 minus the probability that is does occur. P(not A) = P(A ) = 1 − P(A) Tail = not Tail = Head P(Tail ) = 1 − P(Tail) = 0. 5 Venn diagram: Sample space made up of an event A and its complement A , i. e. , everything that is not A.

Birthday Problem • What is the smallest number of people you need in a group so that the probability of 2 or more people having the same birthday is greater than 1/2? • Answer: 23 No. of people 23 30 40 60 Probability. 507. 706. 891. 994

Example: Birthday Problem • A={at least 2 people in the group have a common birthday} • A’ = {no one has common birthday}
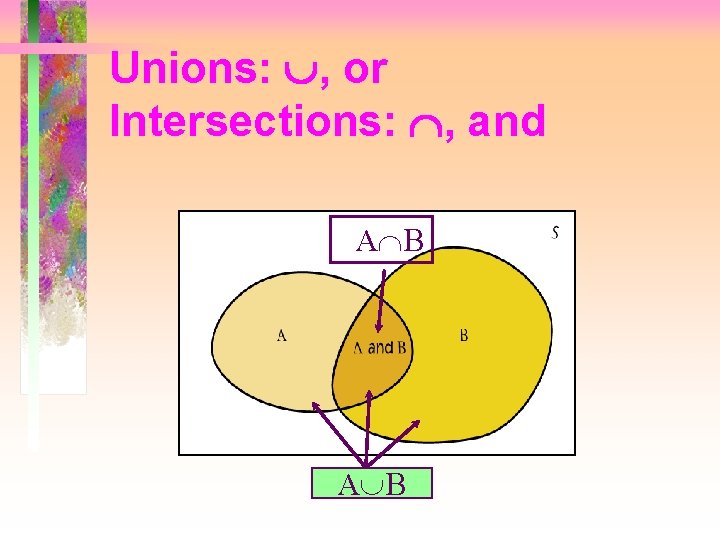
Unions: , or Intersections: , and A B AÈB

Mutually Exclusive (Disjoint) Events Venn Diagrams A and B disjoint: A B= • Mutually exclusive or disjoint events-no outcomes from S in common A B AÈB A and B not disjoint

Laws of Probability - 3 Addition Rule for Disjoint Events 4. If A and B are disjoint events, then P(A or B) = P(A) + P(B)

Laws of Probability - 4 General Addition Rule 5. For any two events A and B P(A or B) = P(A) + P(B) – P(A and B)

General Addition Rule For any two events A and B P(A or B) = P(A) + P(B) - P(A and B) P(A) =6/13 + A P(B) =5/13 _ P(A and B) =3/13 P(A or B) = 8/13 B A or B 22

Laws of Probability - 5 Multiplication Rule 6. For two independent events A and B P(A and B) = P(A) × P(B) Note: assuming events are independent doesn’t make it true.

Multiplication Rule • The probability that you encounter a green light at the corner of Dan Allen and Hillsborough is 0. 35, a yellow light 0. 04, and a red light 0. 61. What is the probability that you encounter a red light on both Monday and Tuesday? • It’s reasonable to assume that the color of the light you encounter on Monday is independent of the color on Tuesday. So P(red on Monday and red on Tuesday) = P(red on Monday) × P(red on Tuesday) = 0. 61 × 0. 61 = 0. 3721

Laws of Probability: Summary • • 1. 0 P(A) 1 for any event A 2. P( ) = 0, P(S) = 1 3. P(A’) = 1 – P(A) 4. If A and B are disjoint events, then P(A or B) = P(A) + P(B) • 5. For any two events A and B, P(A or B) = P(A) + P(B) – P(A and B) 6. For two independent events A and B P(A and B) = P(A) × P(B)

M&M candies If you draw an M&M candy at random from a bag, the candy will have one of six colors. The probability of drawing each color depends on the proportions manufactured, as described here: Color Probability Brown Red Yellow Green Orange Blue 0. 3 0. 2 0. 1 ? What is the probability that an M&M chosen at random is blue? S = {brown, red, yellow, green, orange, blue} P(S) = P(brown) + P(red) + P(yellow) + P(green) + P(orange) + P(blue) = 1 – [P(brown) + P(red) + P(yellow) + P(green) + P(orange)] = 1 – [0. 3 + 0. 2 + 0. 1] = 0. 1 What is the probability that a random M&M is any of red, yellow, or orange? P(red or yellow or orange) = P(red) + P(yellow) + P(orange) = 0. 2 + 0. 1 = 0. 5

Example: college students Suppose 56% of all students live on campus, 62% of all students purchase a campus meal plan and 42% do both. Question: what is the probability that a randomly selected student either lives OR eats on campus. • L= {student lives on campus} • M = {student purchases a meal plan} P(a student either lives or eats on campus) = P(L or M) = P(L) + P(M) - P(L and M) =0. 56 + 0. 62 – 0. 42 = 0. 76

Probability Basics (cont. ) z. Odds and Probabilities z. Probability Trees

ODDS AND PROBABILITIES z. World Series Odds z. From probability to odds z. From odds to probability

From Probability to Odds z If event A has probability P(A), then the odds in favor of A are P(A) to 1 -P(A). It follows that the odds against A are 1 -P(A) to P(A) z If the probability of an earthquake in California is. 25, then the odds in favor of an earthquake are. 25 to. 75 or 1 to 3. The odds against an earthquake are. 75 to. 25 or 3 to 1

From Odds to Probability z If the odds in favor of an event E are a to b, then P(E)=a/(a+b) z in addition, P(E’)=b/(a+b) z If the odds in favor of UNC winning the NCAA’s are 3 (a) to 1 (b), then P(UNC wins)=3/4 P(UNC does not win)= 1/4

Probability Trees A Graphical Method for Complicated Probability Problems

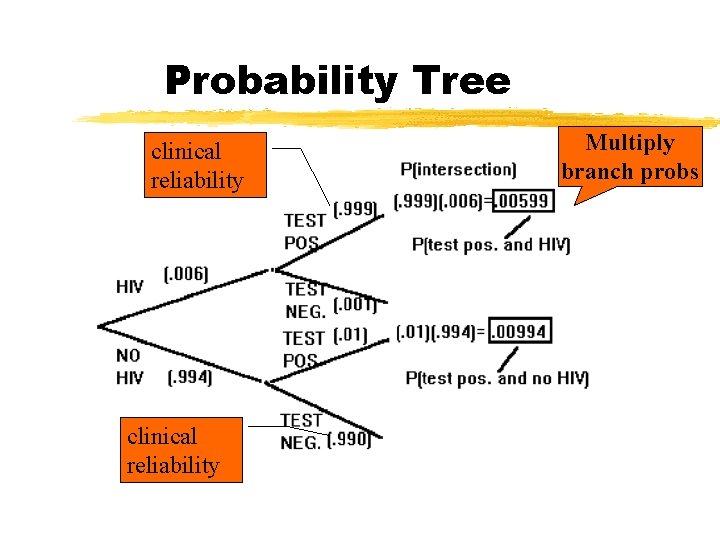
Example: AIDS Testing z V={person has HIV}; CDC: Pr(V)=. 006 z P : test outcome is positive (test indicates HIV present) z N : test outcome is negative z clinical reliabilities for a new HIV test: 1. If a person has the virus, the test result will be positive with probability. 999 2. If a person does not have the virus, the test result will be negative with probability. 990

Question 1 z. What is the probability that a randomly selected person will test positive?
Probability Tree clinical reliability Multiply branch probs

Question 1 Answer z. What is the probability that a randomly selected person will test positive? z. Pr(P )=. 00599 +. 00994 =. 01593

Question 2 z If your test comes back positive, what is the probability that you have HIV? (Remember: we know that if a person has the virus, the test result will be positive with probability. 999; if a person does not have the virus, the test result will be negative with probability. 990). z Looks very reliable

Question 2 Answer two sequences of branches lead to positive test; only 1 sequence represented people who have HIV. Pr(person has HIV given that test is positive) =. 00599/(. 00599+. 00994) =. 376

Summary z. Question 1: z. Pr(P ) =. 00599 +. 00994 =. 01593 z. Question 2: two sequences of branches lead to positive test; only 1 sequence represented people who have HIV. Pr(person has HIV given that test is positive) =. 00599/(. 00599+. 00994) =. 376

Recap z We have a test with very high clinical reliabilities: 1. If a person has the virus, the test result will be positive with probability. 999 2. If a person does not have the virus, the test result will be negative with probability. 990 z But we have extremely poor performance when the test is positive: Pr(person has HIV given that test is positive) =. 376 z In other words, 62. 4% of the positives are false positives! Why? z When the characteristic the test is looking for is rare, most positives will be false.
- Slides: 40