Probability Applications of Counting Principles Finite 8 3

Probability Applications of Counting Principles Finite 8 -3

Have you ever seen or heard the Subway or Starbucks advertising campaigns where they talk about the 10, 000 different combinations of ways to order a sub or drink? Counting Outcomes

Have you ever seen or heard the Subway or Starbucks advertising campaigns where they talk about the 10, 000 different combinations of ways to order a sub or drink? When companies like these make these claims they are using all the different condiments and ways to serve a drink. Counting Outcomes

- These companies can use (2) ideas related to combinations to make these claims: (1) TREE DIAGRAMS (2) THE FUNDAMENTAL COUNTING PRINCIPLE Counting Outcomes

(1) TREE DIAGRAMS A tree diagram is a diagram used to show the total number of possible outcomes in a probability experiment. Counting Outcomes

(2) THE FUNDAMENTAL COUNTING PRINCIPLE The Fundamental Counting Principle uses multiplication of the number of ways each event in an experiment can occur to find the number of possible outcomes in a sample space. Counting Outcomes

Example 1: Tree Diagrams. A new polo shirt is released in 4 different colors and 5 different sizes. How many different color and size combinations are available to the public? Colors – (Red, Blue, Green, Yellow) Styles – (S, M, L, XXL) Counting Outcomes

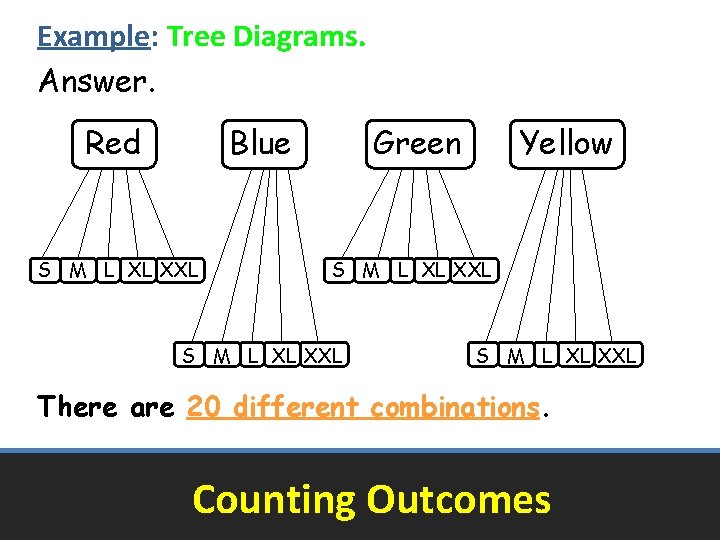
Example: Tree Diagrams. Answer. Red Blue S M L XL XXL Green Yellow S M L XL XXL There are 20 different combinations. Counting Outcomes

Example: The Fundamental Counting Principle. A new polo shirt is released in 4 different colors and 5 different sizes. How many different color and size combinations are available to the public? Colors – (Red, Blue, Green, Yellow) Styles – (S, M, L, XXL) Counting Outcomes

Example: The Fundamental Counting Principle. Answer. Number of Possible Styles 4 Number of Possible Sizes Possible Comb. x 5 = 20 Counting Outcomes

q Tree Diagrams and The Fundamental Counting Principle are two different algorithms for finding sample space of a probability problem. q However, tree diagrams work better for some problems and the fundamental counting principle works better for other problems. Counting Outcomes

Example: Tree Diagram. Tamara spins a spinner two times. What is her probability of spinning a green on the first spin and a blue on the second spin? Counting Outcomes

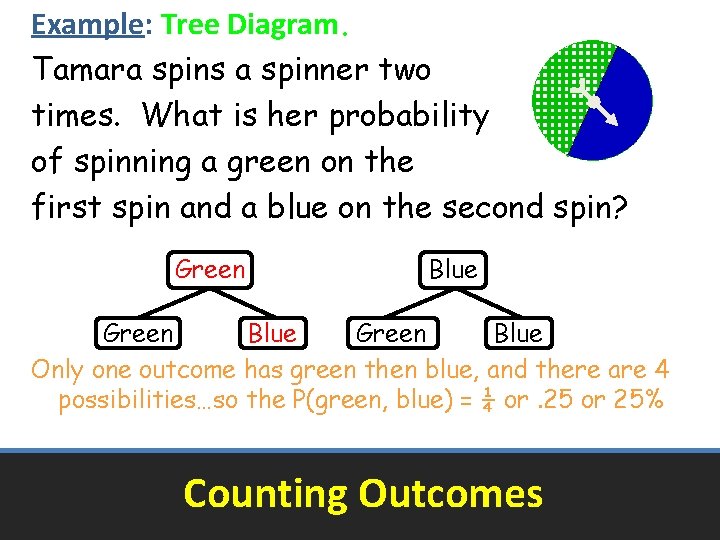
Example: Tree Diagram. Tamara spins a spinner two times. What is her probability of spinning a green on the first spin and a blue on the second spin? Green Blue Only one outcome has green then blue, and there are 4 possibilities…so the P(green, blue) = ¼ or. 25 or 25% Counting Outcomes

Example: The Fundamental Counting Principle. If a lottery game is made up of three digits from 0 to 9, what is the probability of winning the game? Counting Outcomes

Example: The Fundamental Counting Principle. If a lottery game is made up of three digits from 0 to 9, what is the probability of winning if you buy 1 ticket? # of Possible Digits 10 x 10 = # of Possible Outcomes 1000 Because there are 1000 different possibilities, buying one ticket gives you a 1/1000 probability or 0. 001 or 0. 1% chance of winning. Counting Outcomes

Practice: Determine the probability for each problem. (1) How many outfits are possible from a pair of jean or khaki shorts and a choice of yellow, white, or blue shirt? (2) Scott has 5 shirts, 3 pairs of pants, and 4 pairs of socks. How many different outfits can Scott choose with a shirt, pair of pants, and pair of socks? Counting Outcomes

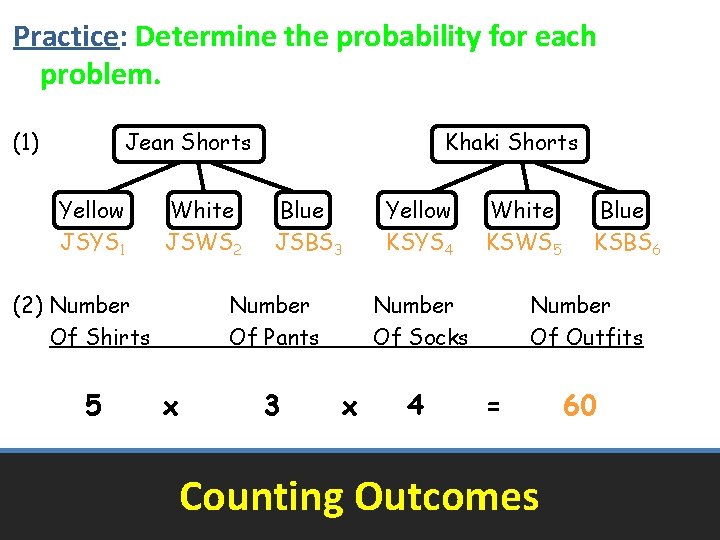
Practice: Determine the probability for each problem. (1) Jean Shorts Yellow JSYS 1 White JSWS 2 (2) Number Of Shirts 5 Khaki Shorts Blue JSBS 3 Number Of Pants x 3 Yellow KSYS 4 White KSWS 5 Number Of Socks x 4 Blue KSBS 6 Number Of Outfits = Counting Outcomes 60

Real World Example: The Fundamental Counting Principle. How many seven digit telephone numbers can be made up using the digits 0 -9, without repetition? Counting Outcomes

Real World Example: The Fundamental Counting Principle. How many seven digit telephone numbers can be made up using the digits 0 -9, without repetition? Answer: 604, 800 different numbers Counting Outcomes

Real World Example: Tree Diagram. Kaitlyn tosses a coin 3 times. Draw a picture showing the possible outcomes. What is the probability of getting at least 2 tails? Counting Outcomes

Real World Example: Tree Diagram. Kaitlyn tosses a coin 3 times. Draw a picture showing the possible outcomes. What is the probability of getting at least 2 tails? Answer: P(at least 2 tails) = ½ Counting Outcomes

Summary: - A tree diagram is used to show all of the possible outcomes, or sample space, in a probability experiment. - The fundamental counting principle can be used to count the number of possible outcomes given an event that can happen in some number of ways followed by another event that can happen in some number of different ways. Counting Outcomes

Summary: So when should I use a tree diagram or the fundamental counting principle? - A tree diagram is used to: (1) show sample space; (2) count the number of preferred outcomes. - The fundamental counting principle can be used to: (1) count the total number of outcomes. Counting Outcomes

Twenty-six slips of paper are each marked with a different letter of the alphabet and placed in a basket. A slip is pulled out, its letter recorded (in the order in which the slip was drawn), and the slip is replaced. This is done 4 times. find the probability that a word with no repetition of letter is formed. Example

Twenty-six slips of paper are each marked with a different letter of the alphabet and placed in a basket. A slip is pulled out, its letter recorded (in the order in which the slip was drawn), and the slip is replaced. This is done 5 times. find the probability that a word starts with "p" Example

• Three crows, 4 blue jays, and 5 starlings sit in a random order on a section of telephone wire. Find the probability that birds of a feather flock together, that is, that all birds of the same type are sitting together Example

• Seven names are put on a ballot in a randomly selected order. What is the probability that they are in alphabetical order? Example

• Heidi Shadix and Boyd Shepherd are among 9 representatives making presentations at the annual sales meeting. The presentations are randomly ordered. Find the probability that Heidi is the first presenter and Boyd is the last presenter. Example

• A controversy arose in 1992 over the Teen Talk Barbie doll, each of which was programmed with four sayings randomly picked from a set of 270 sayings. The controversy ways over the saying, “Math class is tough, ” which some felt gave a negative message toward girls doing well in math. In an interview with Science, a spokeswoman for Mattel, the makers of Barbie, said that “There’s a less than 1 % chance you’re going to get a doll that says math class is tough. ” Is this figure correct? If not, give the correct figure. Example

Homework