Probability and Stochastic Processes A friendly introduction for

Probability and Stochastic Processes A friendly introduction for electrical and computer engineers Chapter 10 Stochastic Processes Dr. Talal Skaik Electrical Engineering department Islamic University of Gaza December 2011 1

• The word stochastic means random. • The word process in this context means function of time. 2

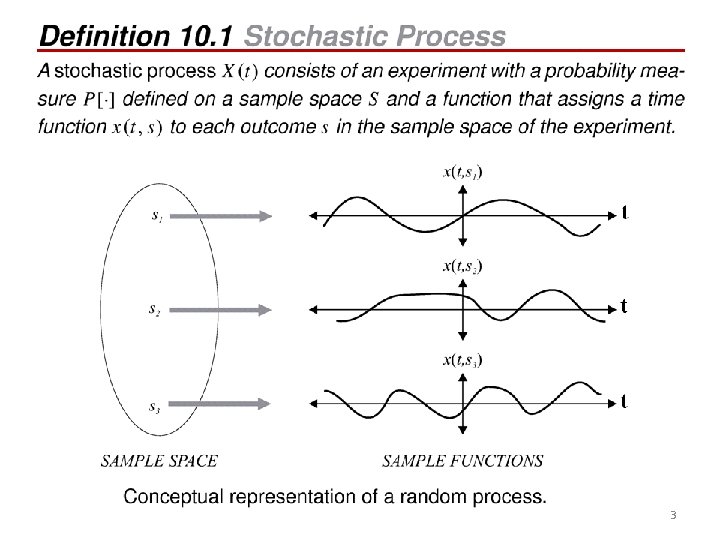
3

Example: random variable in where is a uniformly distributed represents a stochastic process. 4

5

Ensemble average: With t fixed at t=t 0, X(t 0) is a random variable, we have the averages ( expected value and variance) as we studied earlier. Time average: applies to a specific sample function x(t, s 0), and produces a typical number for this sample function. 6

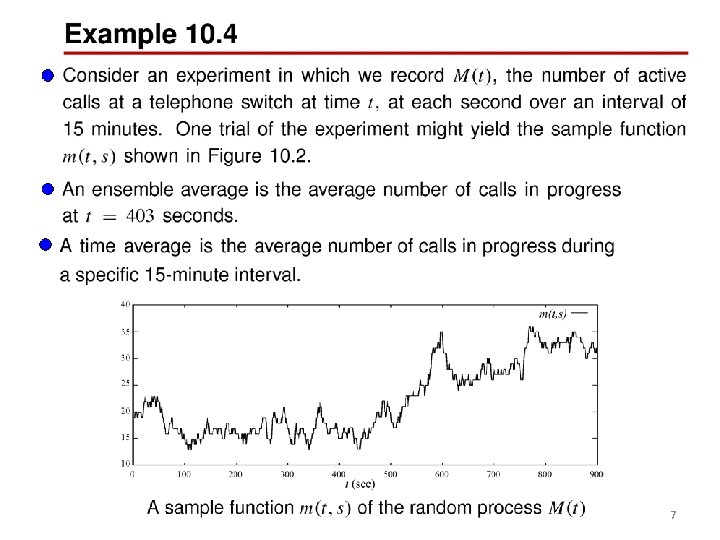
7

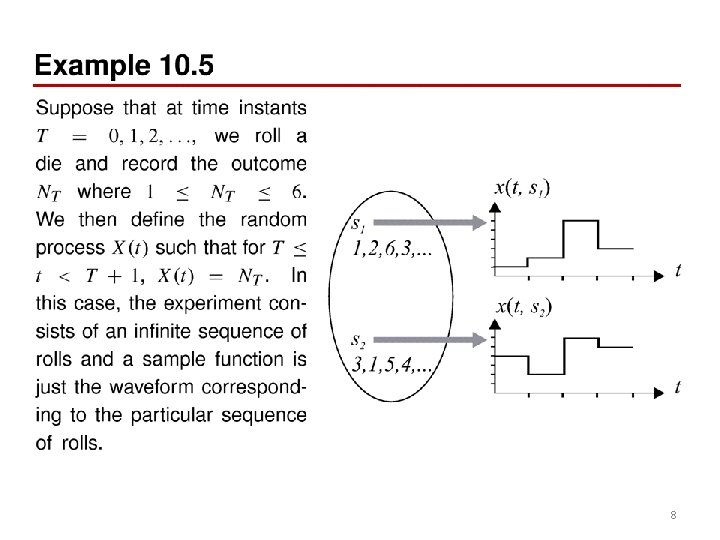
8

9

10

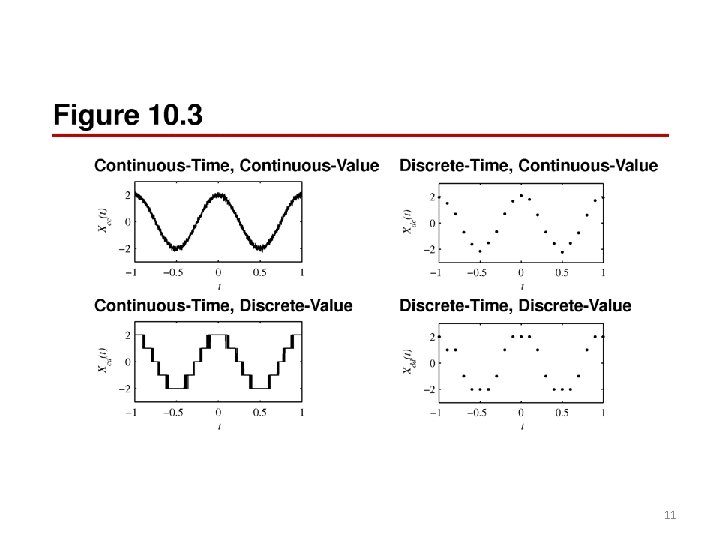
11

12

13

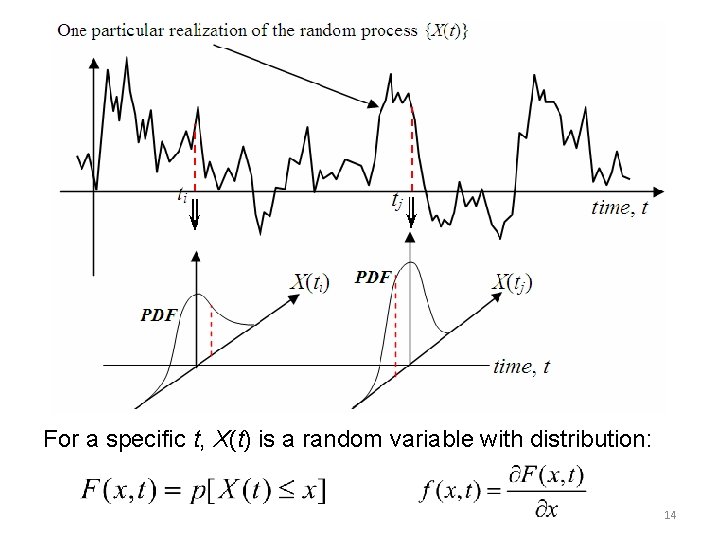
For a specific t, X(t) is a random variable with distribution: 14

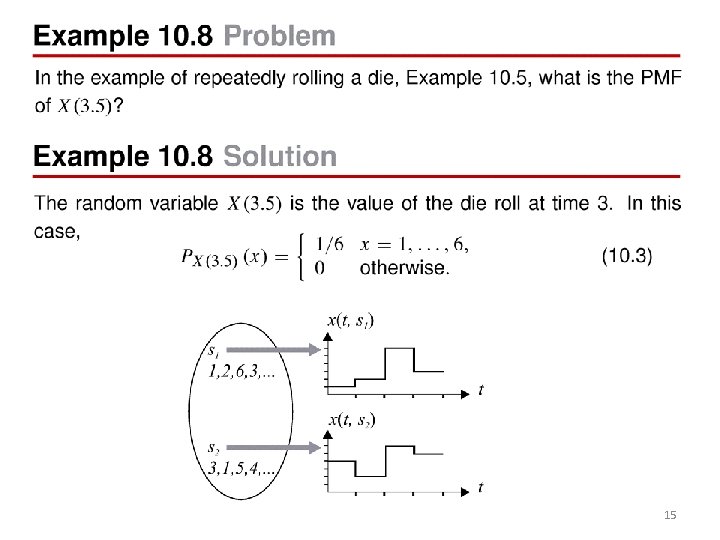
15

16

17

18

19

Autocovariance When Cov[X, Y] is applied to two random variables that are observations of X(t) taken at two different times, t 1 and t 2 =t 1 +τ seconds: ØThe covariance indicates how much the process is likely to change in the τ seconds elapsed between t 1 and t 2. ØA high covariance indicates that the sample function is unlikely to change much in the τ-second interval. ØA covariance near zero suggests rapid change. 20

21

22

ØRecall in a stochastic process X(t), there is a random variable X(t 1) at every time t 1 with PDF f. X(t 1)(x). ØFor most random processes, the PDF f. X(t 1)(x) depends on t 1. ØFor a special class of random processes know as stationary processes, f. X(t 1)(x) does not depend on t 1. ØTherefore: the statistical properties of the stationary process do not change with time (time-invariant). 23

24

25

26