Probability and Information A brief review Data Mining

Probability and Information A brief review Data Mining – Probability 7/03 H Liu (ASU) & G Dong (WSU) Copyright, 1996 © Dale Carnegie & Associates, Inc.

Probability n n Probability provides a way of summarizing uncertainty that comes from our laziness and ignorance - how wonderful it is! Probability, belief of the truth of a sentence n n n 7/03 1 - true, 0 - false, 0<P<1 - intermediate degrees of belief in the truth of the sentence Degree of truth (fuzzy logic) vs. degree of belief Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 2

n All probability statements must indicate the evidence wrt which the probability is being assessed. n n 7/03 Prior or unconditional probability Posterior or conditional probability Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 3

Basic probability notation n Prior probability n n n Proposition: P(Sunny) Random variable: P(Weather=Sunny) Each Random Variable has a domain n n Sunny, Cloudy, Rain, Snow Probability distribution P(Weather) = <. 7, . 2, . 08, . 02> A random variable is not a number; a number may be obtained by observing a RV. A random variable can be continuous or discrete 7/03 Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 4

Conditional Probability n Definition n n Product rule n n P(A|B) = P(A^B)/P(B) P(A^B) = P(A|B)P(B) Probabilistic inference does not work like logical inference. 7/03 Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 5

The axioms of probability n n n All probabilities are between 0 and 1 Necessarily true (valid) propositions have probability 1; false (unsatisfiable) have 0 The probability of a disjunction P(Av. B)=P(A)+P(B)-P(A^B) 7/03 Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 6

The joint probability distribution n Joint completely specifies probability assignments to all propositions in the domain A probabilistic model consists of a set of random variables (X 1, …, Xn). An atomic event is an assignment of particular values to all the variables. Marginalization rule for RV Y and Z: n P(Y) = ΣP(Y, z) over z Let’s see an example next. n n n 7/03 Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 7

Joint Probability n n n An example of two Boolean variables Observations: mutually exclusive and collectively exhaustive What are P(Cavity) = P(Cavity V Toothache) = P(Cavity ^ Toothache) = P(Cavity|Toothache) = 7/03 Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 8

Bayes’ rule n Deriving the rule via the product rule n n n P(B|A) = P(A|B)P(B)/P(A) can be viewed as a normalization factor that makes P(B|A) + (!B|A) = 1 P(A) = P(A|B)P(B)+P(A|!B)P(!B) A more general case is P(X|Y) = P(Y|X)P(X)/P(Y) n Bayes’ rule conditionalized on evidence E P(X|Y, E) = P(Y|X, E)P(X|E)/P(Y|E) 7/03 Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 9

Independence n Independent events A, B n n P(B|A)=P(B), P(A|B)=P(A), P(A, B)=P(A)P(B) Conditional independence n 7/03 P(X|Y, Z)=P(X|Z) – given Z, X and Y are independent Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 10

Entropy n n n Entropy measures homogeneity/purity of sets of examples Or as information content: the less you need to know (to determine class of new case), the more information you have With two classes (P, N) in S, p & n instances; let t=p+n. View [p, n] as class distribution of S. n n n 7/03 Entropy(S) = - (p/t) log 2 (p/t) - (n/t) log 2 (n/t) E. g. , p=9, n=5; Entropy(S) = Entropy([9, 5]) = - (9/14) log 2 (9/14) - (5/14) log 2 (5/14) = 0. 940 E. g. , Entropy([14, 0])=0; Entropy([7, 7])=1 Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 11
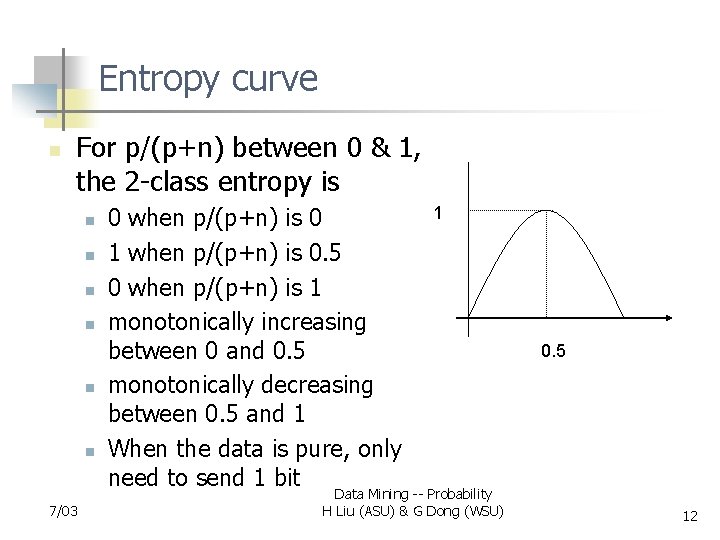
Entropy curve n For p/(p+n) between 0 & 1, the 2 -class entropy is n n n 7/03 0 when p/(p+n) is 0 1 when p/(p+n) is 0. 5 0 when p/(p+n) is 1 monotonically increasing between 0 and 0. 5 monotonically decreasing between 0. 5 and 1 When the data is pure, only need to send 1 bit 1 Data Mining -- Probability H Liu (ASU) & G Dong (WSU) 0. 5 12
- Slides: 12