Probability and inference General probability rules IPS chapter

Objectives (IPS chapter 4. 5) General probability rules p General addition rules p Conditional probability p General multiplication rules p Probability trees p Bayes’s rule

General addition rules General addition rule for any two events A and B: The probability that A occurs, or B occurs, or both events occur is: P(A or B) = P(A) + P(B) – P(A and B) Disjoint => P(A and B) = 0 What is the probability of randomly drawing either an ace or a heart from a deck of 52 playing cards? There are 4 aces in the pack and 13 hearts. However, 1 card is both an ace and a heart. Thus: P(ace or heart) = P(ace) + P(heart) – P(ace and heart) = 4/52 + 13/52 - 1/52 = 16/52 ≈. 3

Conditional probability Conditional probabilities reflect how the probability of an event can change if we know that some other event has occurred/is occurring. p Example: The probability of rain is different if you live in Los Angeles than if you live in Seattle. p Our brains calculate conditional probabilities, updating our sense of chance with each new piece of evidence. The conditional probability of event B given event A is: (provided that P(A) ≠ 0)

General multiplication rules p The probability that any two events, A and B, both occur is: P(A and B) = P(A)P(B|A) This is the general multiplication rule. p If A and B are independent, then P(A and B) = P(A)P(B) (If A and B are independent then P(B|A) is just P(B). ) What is the probability of randomly drawing either an ace of heart from a deck of 52 playing cards? There are 4 aces in the pack and 13 hearts. P(heart|ace) = 1/4 P(ace) = 4/52 èP(ace and heart) = P(ace)* P(heart|ace) = (4/52)*(1/4) = 1/52 Notice that heart and ace are independent events.

Probability trees Conditional probability calculations can get complex, and it is often a good strategy to build a probability tree that represents all possible outcomes graphically and assigns conditional probabilities to subsets of events. Tree diagram for chat room habits for three adult age groups Internet user 0. 47 P(chatting) = 0. 136 + 0. 099 + 0. 017 = 0. 252 About 25% of all adult Internet users visit chat rooms.

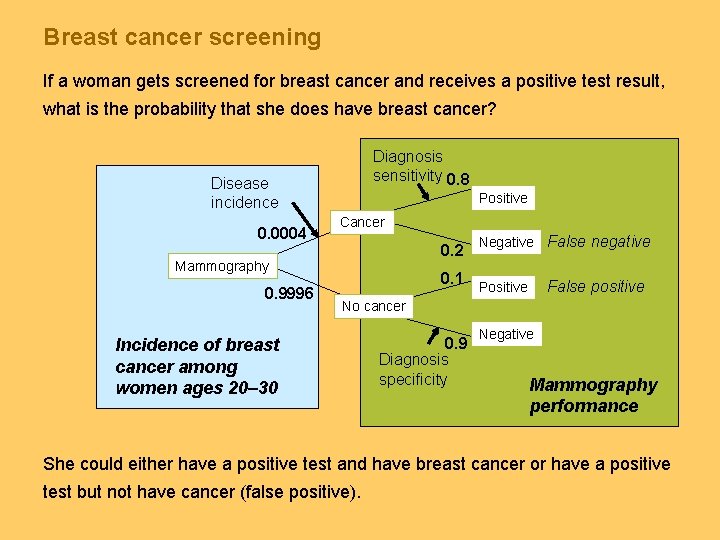
Breast cancer screening If a woman gets screened for breast cancer and receives a positive test result, what is the probability that she does have breast cancer? Diagnosis sensitivity 0. 8 Disease incidence 0. 0004 Positive Cancer 0. 2 Mammography 0. 9996 0. 1 Negative False negative False positive Positive No cancer Incidence of breast cancer among women ages 20– 30 0. 9 Diagnosis specificity Negative Mammography performance She could either have a positive test and have breast cancer or have a positive test but not have cancer (false positive).

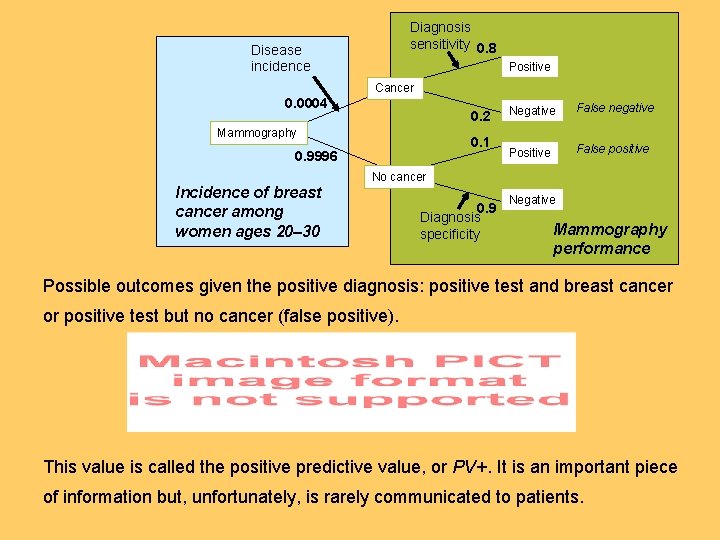
Diagnosis sensitivity 0. 8 Disease incidence Positive Cancer 0. 0004 0. 2 Mammography 0. 1 0. 9996 Negative False negative Positive False positive No cancer Incidence of breast cancer among women ages 20– 30 0. 9 Diagnosis specificity Negative Mammography performance Possible outcomes given the positive diagnosis: positive test and breast cancer or positive test but no cancer (false positive). This value is called the positive predictive value, or PV+. It is an important piece of information but, unfortunately, is rarely communicated to patients.

Bayes’s rule One application of the previous result is known as Bayes’ rule. • If a sample space may be partitioned into k disjoint events, A 1, A 2, … , Ak — P(A 1) + P(A 2) + … + P(Ak) = 1, However, it is often much easier to work out answers with a probability tree than with the formula above.

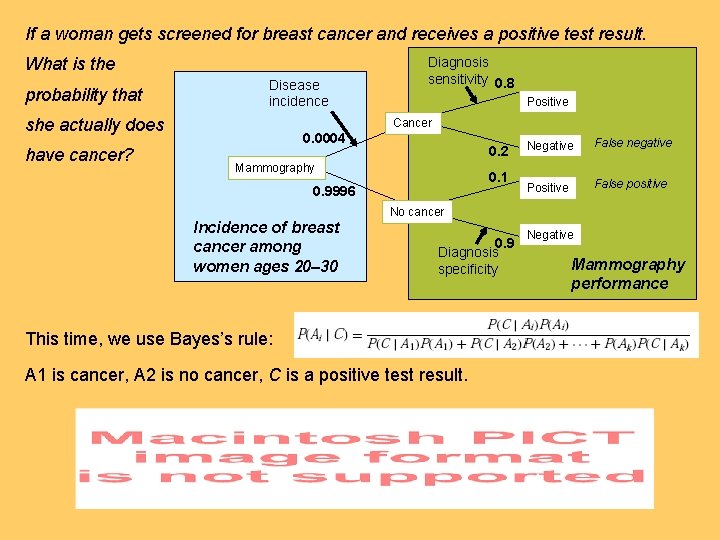
If a woman gets screened for breast cancer and receives a positive test result. What is the probability that Disease incidence she actually does have cancer? Diagnosis sensitivity 0. 8 Positive Cancer 0. 0004 0. 2 Mammography 0. 1 0. 9996 Negative False negative Positive False positive No cancer Incidence of breast cancer among women ages 20– 30 0. 9 Diagnosis specificity This time, we use Bayes’s rule: A 1 is cancer, A 2 is no cancer, C is a positive test result. Negative Mammography performance