Probability and Contingency Tables Contingency table Suppose that

Probability and Contingency Tables

Contingency table Suppose that we have two variables, gender (male or female) and right or left handedness. l Population sampled = 100 l How can we write the results in a way that helps us display the data? l Data distribution can be written in a contingency table l Right Handed Left Handed Totals Males 43 9 52 Females 44 4 48 TOTALS 87 13 100

Gender and L or R handed Right Handed Left Handed Totals Males 43 9 52 Females 44 4 48 TOTALS 87 13 100 What is the probability one of the participants is a female? (# females/Total) What is the probability someone is left handed ? (total left hand/ total) What is the probability someone is a left handed male? (# of left handed males / total)

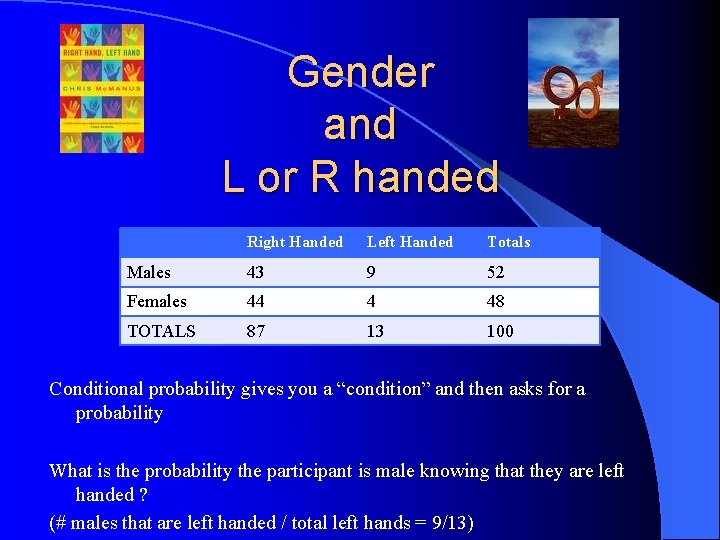
Gender and L or R handed Right Handed Left Handed Totals Males 43 9 52 Females 44 4 48 TOTALS 87 13 100 Conditional probability gives you a “condition” and then asks for a probability What is the probability the participant is male knowing that they are left handed ? (# males that are left handed / total left hands = 9/13)

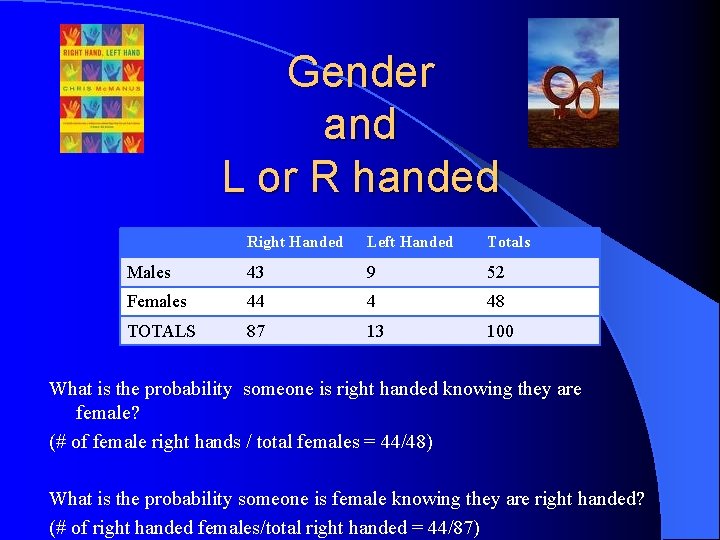
Gender and L or R handed Right Handed Left Handed Totals Males 43 9 52 Females 44 4 48 TOTALS 87 13 100 What is the probability someone is right handed knowing they are female? (# of female right hands / total females = 44/48) What is the probability someone is female knowing they are right handed? (# of right handed females/total right handed = 44/87)

Probability P(A) = part/whole A = male wearing green P(A) = 2/15 B = wearing red P(B) given they are women

Probability P(A) = part/whole C = they are wearing red If they are all men, what is P(C)? D = they are women Gven they are wearing green,

How to complete a contingency table Total All outcomes

Use the subtotals and information given Total Subtotal of 1 rst row Subtotal of 2 nd row Total Subtotal of 1 rst column Subtotal of 2 nd column All outcomes

Use the subtotals and information given Black Red Total Bugetti veron 7 3 Subtotal of 1 rst row 10 Ferrari 5 35 Subtotal of 2 nd row 40 Total Subtotal of 1 rst column Subtotal of 2 nd column All outcomes 50 12 38

Conditional Probability P(A | B) : l. A and B are two events, l the conditional probability that A occurs given that B already has l “P(A | B)”

What is the probability that the car is a Ferrari, given that it is black? Black Red Total Bugetti veron 7 3 Subtotal of 1 rst row 10 Ferrari 5 35 Subtotal of 2 nd row 40 Total Subtotal of 1 rst column Subtotal of 2 nd column All outcomes 50 12 38

What is the probability that the car is black given that it is a Bugetti Veron? Black Red Total Bugetti veron 7 3 Subtotal of 1 rst row 10 Ferrari 5 35 Subtotal of 2 nd row 40 Total Subtotal of 1 rst column Subtotal of 2 nd column All outcomes 50 12 38

A frog climbing out of a well is affected by the weather. l When it rains, he falls back down the well with a probability of 1/10. l In dry weather, he only falls back down with probability of 1/25. l The probability of rain is 1/5 (therefore the probability it won’t rain is 4/5). l

Complimentary events A and A (A + A = 1) l Events are complimentary when their probability adds up to one l They complement each other meaning if one doesn’t happen the other will. Example: There are 30 skittles (of course!) _ 10 yellow, 10 green l 10 red, l Event A is getting a green P(A) = 10/30 or 1/3 l Event A is not getting green P(A) = 20/30 or 2/3 l

Example: Will the Frog Fall? l The probability of rain is 1/5 – l P(R) = 1/5 Therefore: the probability it won’t rain is 4/5 – _P(R) = 4/5 l l P of falling when it rained is 1/10 – l The P of not falling when it rained is 9/10 The P of falling when it’s dry is 1/25 – The P of not falling when it’s dry is 24/25

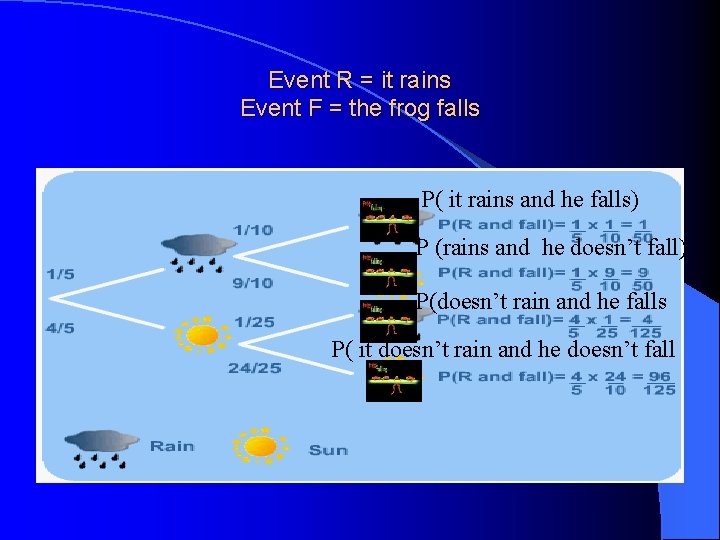
Event R = it rains Event F = the frog falls P( it rains and he falls) P (rains and he doesn’t fall) P(doesn’t rain and he falls P( it doesn’t rain and he doesn’t fall