Probability 14 1 Experimental Probability 14 2 Principles

Probability 14. 1 Experimental Probability 14. 2 Principles of Counting 14. 4 Theoretical Probability Copyright © 2012, 2009, and 2006, Pearson Education, Inc.

14. 1 Experimental Probability Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -2

DEFINITION: EXPERIMENTAL PROBABILITY Suppose an experiment with a number of possible outcomes is performed repeatedly – say, n times – and that a specific outcome E occurs r times. The experimental (or empirical or experiential) probability, denoted by , that E will occur on any given trial of the experiment is given by Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -3

THE LAW OF LARGE NUMBERS If an experiment is performed repeatedly, the experimental probability of a particular outcome more and more closely approximates a fixed number as the number of trials increases. Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -4
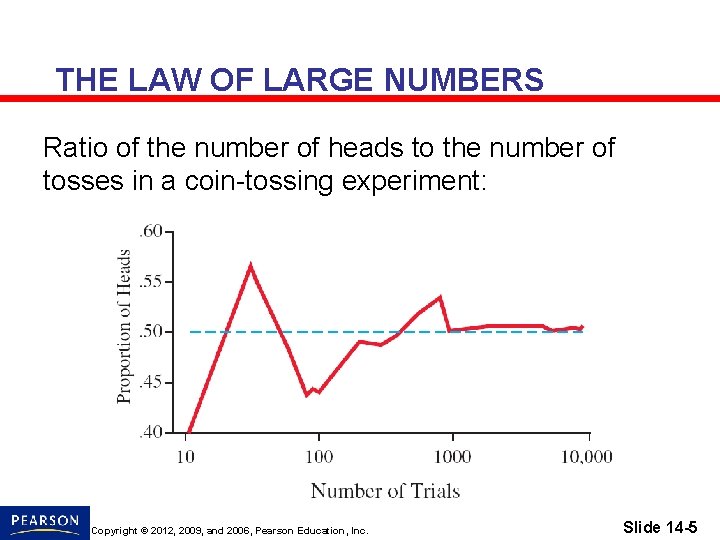
THE LAW OF LARGE NUMBERS Ratio of the number of heads to the number of tosses in a coin-tossing experiment: Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -5

Example 14. 3: Computing Experimental Probability from Data The final examination scores of students in a precalculus class are as shown. Compute the experimental probability that a student chosen at random from the class had a score in the 70 s? Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -6

Example 14. 3: continued Since 6 of the 28 students scored in the 70 s, the experimental probability that a student chosen at random had a score in the 70 s is Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -7

Example 14. 4: Determining Experimental Probabilities from an Experiment Christine has five pennies. She is curious how often she should expect to see at most one head when all five coins are flipped onto the floor. To find an answer, she repeatedly flips the five pennies and counts the number of heads that turn up. After repeating the experiment 50 times, she obtains the following frequency table: Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -8

Example 14. 4: continued On the basis of Christine’s data, what is the experimental probability that a flip of five coins results in at most one head? The data shows that exactly one head appeared on seven of the trials ad no heads appeared once. This means that the outcome of at most one head occurred 1 + 7 = 8 times in the 50 trials, giving the experimental probability of Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -9

THE TERMINOLOGY OF PROBABILITY OUTCOME: a result of one trial of an experiment SAMPLE SPACE S: the set of all outcomes of an experiment EVENT E: a set E of some of the outcomes of the experiment (that is, a subset E of the sample space S, so that ) Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -10

THE TERMINOLOGY OF PROBABILITY MUTUALLY EXCLUSIVE EVENTS A and B: two events A and B cannot happen at the same time. Ex. Tossing a coin, the result can be either heads or tails but not both. (that is, A and B are disjoint subsets of the sample space, ) Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -11

EXPERIMENTAL PROBABILITY OF MUTUALLY EXCLUSIVE EVENTS If A and B are mutually exclusive events, then Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -12

DEFINITION: INDEPENDENT EVENTS Events A and B are independent events if the occurrence or nonoccurrence of event A does not affect the occurrence or nonoccurrence of event B, and vice versa. Ex. Drawing an ace and flipping a heads on a coin. Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -13

EXPERIMENTAL PROBABILITY OF INDEPENDENT EVENTS A AND B If A and B are independent events, then Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -14

14. 2 Principle of Counting Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -15

PRINCIPLES OF COUNTING To determine theoretical probabilities of events, we will need to determine Thus, the calculation of theoretical probability is a matter of counting. Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -16

MULTIPLICATION PRINCIPLE OF COUNTING FOR INDEPENDENT EVENTS Let A be a set of outcomes of Stage 1 and B a set of outcomes of Stage 2. If A and B are independent events, then the number of ways that A and B can occur in a two-stage experiment is given by Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -17

Example 14. 14: Counting the Number of Ways to Draw Two Aces How many ways can two aces be drawn in succession from a deck of ordinary cards -- With replacement? If we replace the drawn card, then each choice is independent, so Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -18

Example 14. 14: continued How many ways can two aces be drawn in succession from a deck of ordinary cards -- Without replacement? If we don’t replace the first drawn ace, then the number of ways to draw a second ace is impacted. So Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -19

14. 4 Theoretical Probability Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -20

DEFINITION: THEORETICAL PROBABILITY Let S, the sample space, denote the set of equally likely outcomes of an experiment, and let E, an event, denote a subset of outcomes of the experiment. Let n(S) and n(E) denote the number of outcomes in S and E, respectively. The probability of E, denoted by P(E), is given by Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -21

DETERMINING PROBABILITY Determine the probability of obtaining a total score of 3 or 4 on a single throw of two dice. List the sample space as ordered pairs. (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -22

PROPERTIES OF PROBABILITY 1. 2. 3. For any event Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -23

DEFINITION: ODDS Let A be an event and let complementary event. be the Then the odds in favor of A are and the odds against A are Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -24

Example 14. 34: Determining the Odds in Favor of Rolling a 7 or an 11 In the game of craps, one wins on the first roll of the pair of dice if a 7 or an 11 is thrown. What are the odds of winning on the first roll? Let W be the set of outcomes that result 7 or 11. Since W = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1), (5, 6), (6, 5)} and these are 36 ways two dice can come up, n(W) = 8, and = 36 – 8 = 28. Thus the odds in favor of W are 8 to 28 or, 2 to 7. Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -25

DEFINITION: EXPECTED VALUE OF GAMBLING Average expected payoff in the long run. positive results = win, negative results = loss, zero = breakeven. EV = P(win) x gain – P(lose) x loss Gain = Winnings – Initial Bet Slide 14 -26

DEFINITION: EXPECTED VALUE OF GAMBLING You pay $2 to play the game, if you pull an ace from a deck you win $10, what is the expected value? EV = (4/52)(8) – (48/52)(2) EV = 0. 6154 – 1. 8462 EV = -1. 2308 Should you play this game? If you play it 100 times what will the results be? Slide 14 -27

14. 1 – 14. 2 – 14. 4 Practice 14. 1 – Pages 729 – 732 Q 1, 2, 4, 6, 8, 17, 18, 33 14. 2 – Pages 741 – 743 Q 1, 2, 3, 5, 6, 7, 10, 11 14. 4 – Pages 763 – 765 Q 1, 4, 7, 8, 10, 13, 14 Copyright © 2012, 2009, and 2006, Pearson Education, Inc. Slide 14 -28
- Slides: 28