PROBABILITY 12 C TWO WAY TABLES AND TREE

PROBABILITY 12 C TWO WAY TABLES AND TREE DIAGRAMS

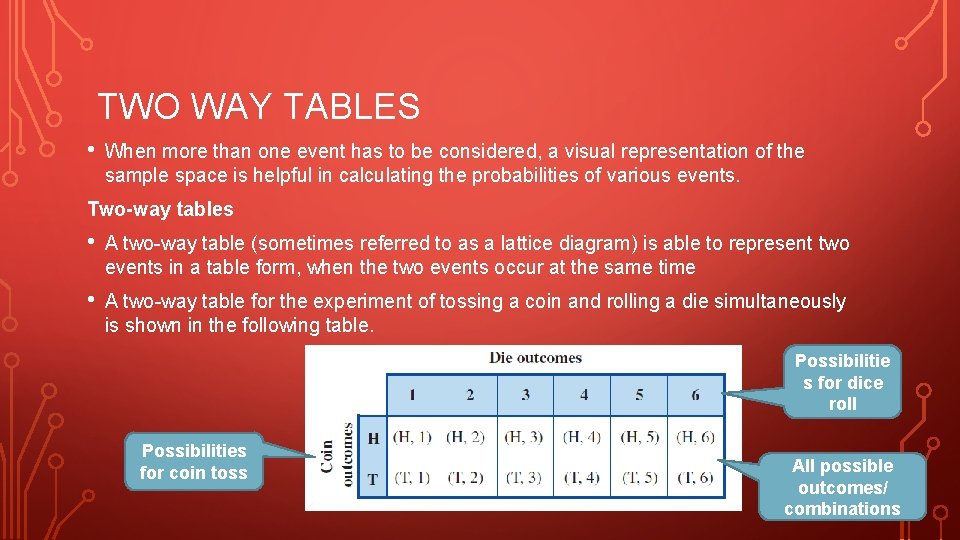
TWO WAY TABLES • When more than one event has to be considered, a visual representation of the sample space is helpful in calculating the probabilities of various events. Two-way tables • A two-way table (sometimes referred to as a lattice diagram) is able to represent two events in a table form, when the two events occur at the same time • A two-way table for the experiment of tossing a coin and rolling a die simultaneously is shown in the following table. Possibilitie s for dice roll Possibilities for coin toss All possible outcomes/ combinations

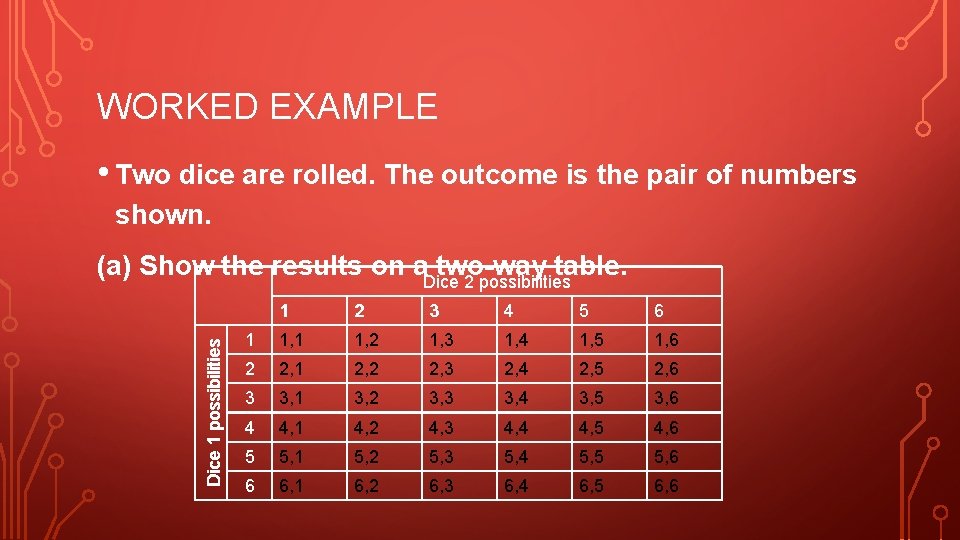
WORKED EXAMPLE • Two dice are rolled. The outcome is the pair of numbers shown. Dice 1 possibilities (a) Show the results on a. Dice two-way table. 2 possibilities 1 2 3 4 5 6 1 1, 2 1, 3 1, 4 1, 5 1, 6 2 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 3 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 4 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 5 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 6 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6

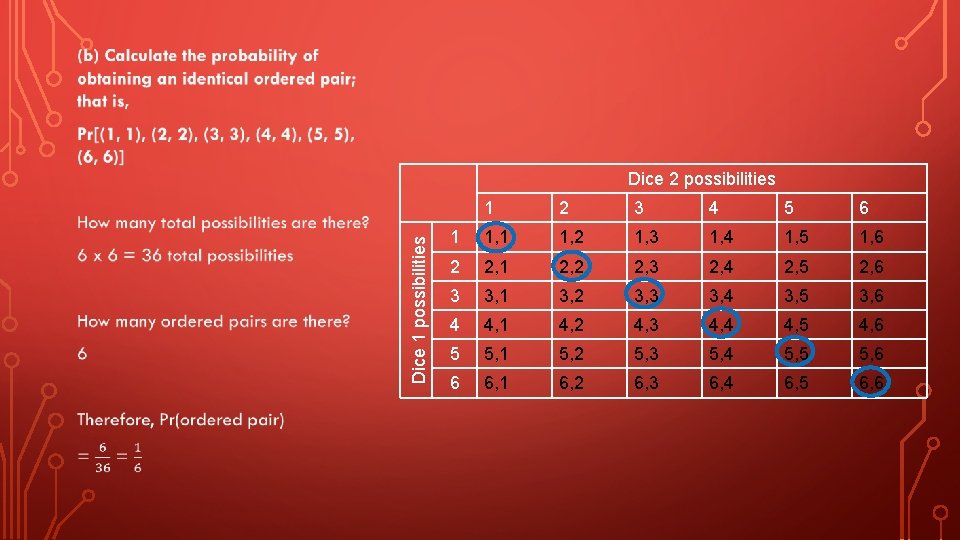
• Dice 1 possibilities Dice 2 possibilities 1 2 3 4 5 6 1 1, 2 1, 3 1, 4 1, 5 1, 6 2 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 3 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 4 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 5 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 6 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6

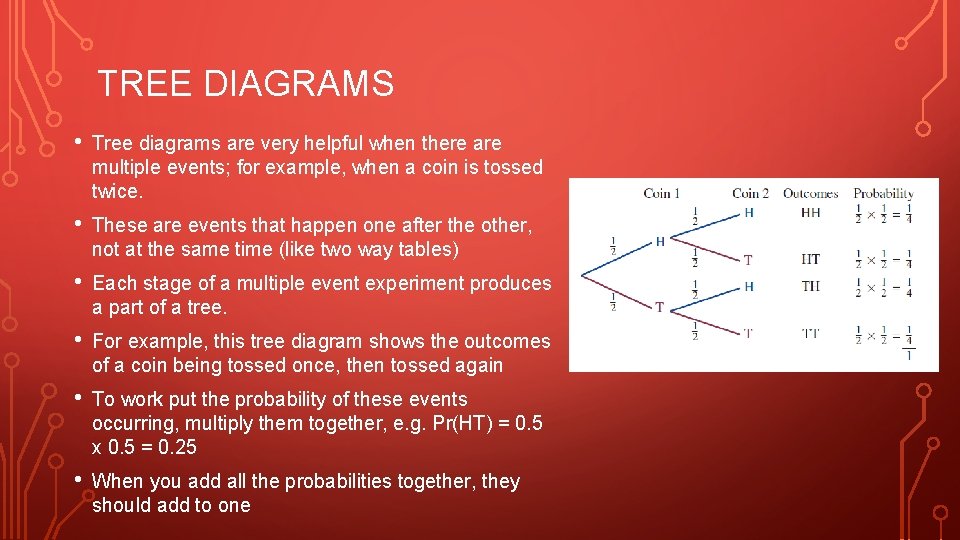
TREE DIAGRAMS • Tree diagrams are very helpful when there are multiple events; for example, when a coin is tossed twice. • These are events that happen one after the other, not at the same time (like two way tables) • Each stage of a multiple event experiment produces a part of a tree. • For example, this tree diagram shows the outcomes of a coin being tossed once, then tossed again • To work put the probability of these events occurring, multiply them together, e. g. Pr(HT) = 0. 5 x 0. 5 = 0. 25 • When you add all the probabilities together, they should add to one

WORKED EXAMPLE • Three coins are tossed simultaneously. Draw a tree diagram for the experiment. Calculate the following probabilities. • a Pr(3 Heads) b Pr(2 Heads) c Pr(at least 1 Head)

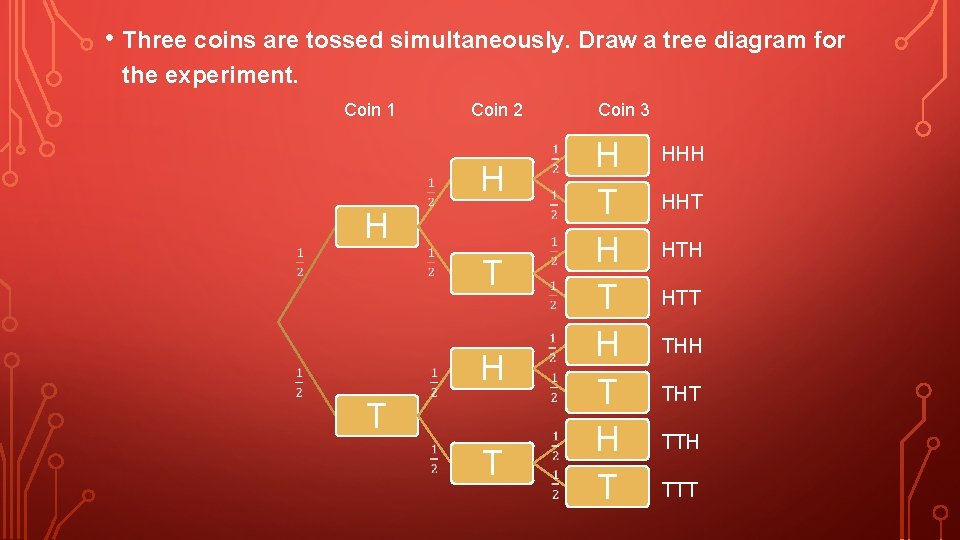
• Three coins are tossed simultaneously. Draw a tree diagram for the experiment. Coin 1 Coin 2 H H T T Coin 3 H T H T HHH HHT HTH HTT THH THT TTH TTT

WORKED EXAMPLE • The letters A, B, C and D are written on identical pieces of card and placed in a box. A letter is drawn at random from the box. Without replacing the first card, a second one is drawn. Use a tree diagram to find: a Pr(first letter is A) b Pr(second letter is B) c Pr(both letters are the same).

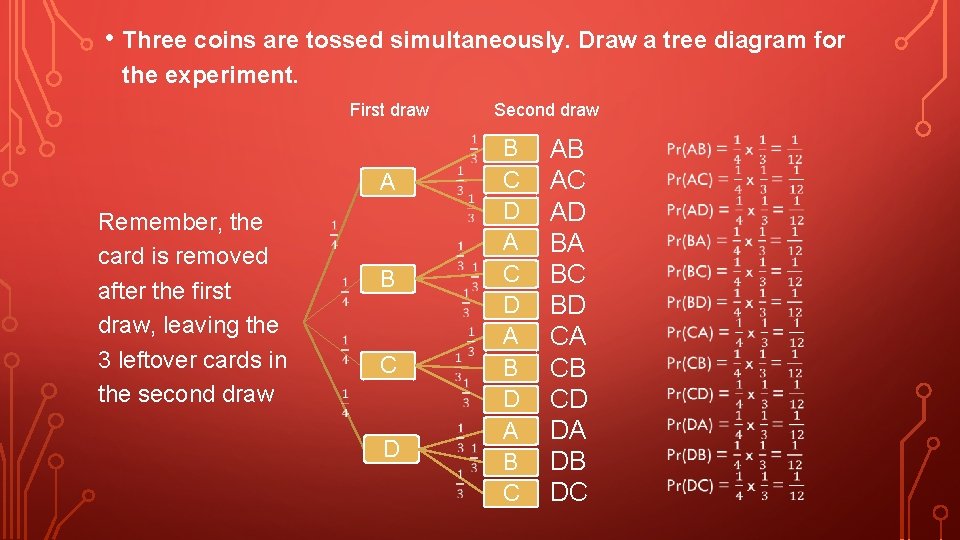
• Three coins are tossed simultaneously. Draw a tree diagram for the experiment. First draw A Remember, the card is removed after the first draw, leaving the 3 leftover cards in the second draw B C D Second draw B C D A B C AB AC AD BA BC BD CA CB CD DA DB DC

• (c) Pr(both letters the same) = Pr(AA) + Pr(BB) + Pr(CC) + Pr(DD) =0

QUESTIONS TO DO • Exercise 12 C p 410: 1, 3, 7, 8, 10, 11, 12