Probabilitas dan Statistika Deskriptif Ukuran Dispersi Range Standar

Probabilitas dan Statistika Deskriptif Ukuran Dispersi Range, Standar Deviasi Oleh: Chaerul Anwar, MTI

Objective • Mahasiswa mampu menjelaskan ukuran dispersi, penggunaaan ukuran dispersi dalam statistika • Mampu menggunakan bagian dari ukuran dispersi seperti : ▫ ▫ ▫ ▫ Range Deviasi Rata – rata Varian Deviasi standar Range inter-kuartil Deviasi kuartil

Pendahuluan • Ukuran penyebaran ▫ Suatu ukuran baik parameter atau statistik untuk mengetahui seberapa besar penyimpangan data dengan nilai rata – rata hitungnya • Ukuran penyebaran mencakup data ▫ Ungrouped data �Data yang belum dikelompokan ▫ Grouped data �Data yang telah dikelompokan ; Tabel distribusi frekuensi

Ukuran Dispersi • Ukuran dispersi adalah ukuran variasi atau seberapa jauh nilai tersebar satu dengan lainnya dari gugus data. • Aplikasi ukuran dispersi yang sering digunakan adalah standar deviasi. • Ukuran dispersi biasanya digunakan bersamaan dengan tendensi sentral untuk mempelajari distribusi data.

Ukuran Dispersi • Range (Jangkauan Data) – interval terkecil yang memuat semua data. Didapat dengan mencari selisih nilai maksimum dengan nilai minimum. • Standar deviasi – menunjukkan seberapa jauh deviasi data pada suatu gugus dari nilai tengahnya. • Varians – menunjukkan seberapa jauh penyebaran satu nilai dengan nilai yang lain pada gugus data. • Kuartil & Jangkauan antar kuartil – memecahkan data menjadi empat bagian yang rata.

Ukuran Dispersi • Rentang • Kuartil • Jangkauan Antar Kuartil • Persentil • Jumlah & Interval Kelompok • Standar Deviasi

Ukuran Penyebaran Untuk Data Tidak Dikelompokan • Range – Jarak ▫ Merupakan perbedaan antara nilai terbesar dan terkecil dalam suatu kelompok data baik data populasi atau sampel • Rumusan Range = Nilai terbesar – nilai terkecil Perusahaan Harga Saham Sentul City 530 Tunas Baru 580 proteinprima 650 total 750 Mandiri 840 Range = 840 – 530 = 310

Rentang • Merupakan ukuran dispersi yg merupakan selisih nilai maksimum dan minimum. Rentang = data terbesar – data terkecil

Deviasi Rata – rata Populasi • Rata – rata hitung dari nilai mutlak deviasi antara nilai data pengamatan dengan rata-rata hitungnya • Rumusan Deviasi rata –rata ( MD) ∑|x - x| MD = N X = Nilai data pengamatan X = Rata – rata hitung N = Jumlah data

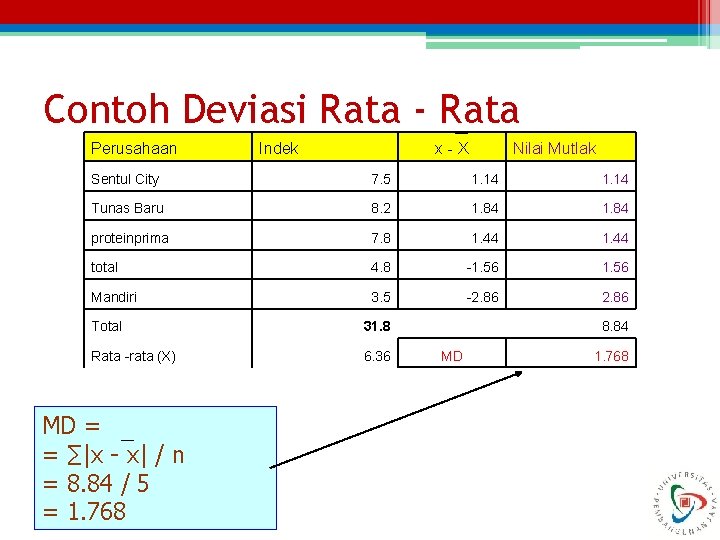
Contoh Deviasi Rata - Rata Perusahaan Indek x-X Nilai Mutlak Sentul City 7. 5 1. 14 Tunas Baru 8. 2 1. 84 proteinprima 7. 8 1. 44 total 4. 8 -1. 56 Mandiri 3. 5 -2. 86 Total 31. 8 Rata -rata (X) 6. 36 MD = = ∑|x - x| / n = 8. 84 / 5 = 1. 768 8. 84 MD 1. 768

Varians dan Standar Deviasi Populasi • Varians ▫ Rata – rata hitung deviasi kuadrat setiap data terhadap rata – rata hitungnya • Rumus varians populasi (X - µ )2 2= N / ) X (∑ N µ = X = Nilai data pengamatan µ = Nilai rata – rata hitung N = Jumlah total data

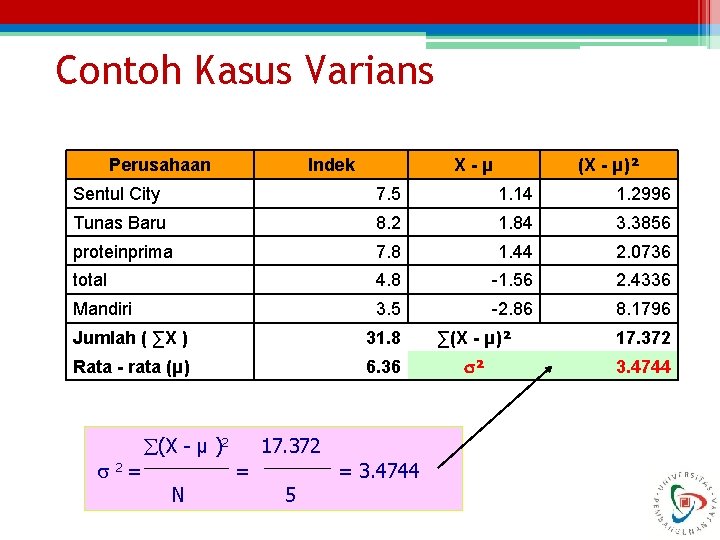
Contoh Kasus Varians Perusahaan X-µ Indek (X - µ)² Sentul City 7. 5 1. 14 1. 2996 Tunas Baru 8. 2 1. 84 3. 3856 proteinprima 7. 8 1. 44 2. 0736 total 4. 8 -1. 56 2. 4336 Mandiri 3. 5 -2. 86 8. 1796 Jumlah ( ∑X ) 31. 8 ∑(X - µ)² 17. 372 Rata - rata (µ) 6. 36 s² 3. 4744 (X - µ )2 17. 372 2 = N = = 3. 4744 5

Standar Deviasi • Standar deviasi ▫ Akar kuadrat dari varians dan menunjukan standar penyimpangan data terhadap nilai rata -ratanya • Rumus standar deviasi (X - µ )2 = N atau = ²

Contoh Kasus Standar Deviasi Nilai varians : (X - µ )2 17. 372 2 = = = 3. 4744 N 5 Nilai standar deviasi : = 3. 4744 = 1. 864 Nilai penyimpangan sebesar 1. 864

Varians dan Standar Deviasi Sampel • Varians (x - x )2 s 2= n -1 • Standar deviasi S = s²

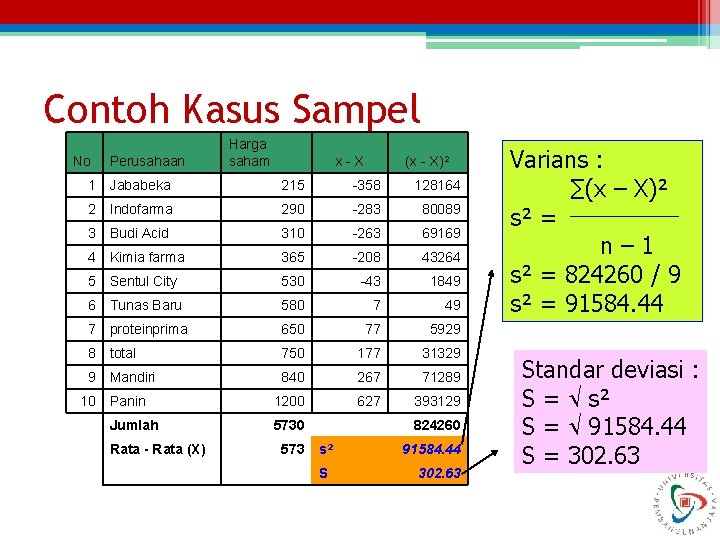
Contoh Kasus Sampel No Perusahaan Harga saham x-X (x - X)² 1 Jababeka 215 -358 128164 2 Indofarma 290 -283 80089 3 Budi Acid 310 -263 69169 4 Kimia farma 365 -208 43264 5 Sentul City 530 -43 1849 6 Tunas Baru 580 7 49 7 proteinprima 650 77 5929 8 total 750 177 31329 9 Mandiri 840 267 71289 Panin 1200 627 393129 Jumlah 5730 10 Rata - Rata (X) 573 s² S 824260 91584. 44 302. 63 Varians : ∑(x – X)² s² = n – 1 s² = 824260 / 9 s² = 91584. 44 Standar deviasi : S = s² S = 91584. 44 S = 302. 63

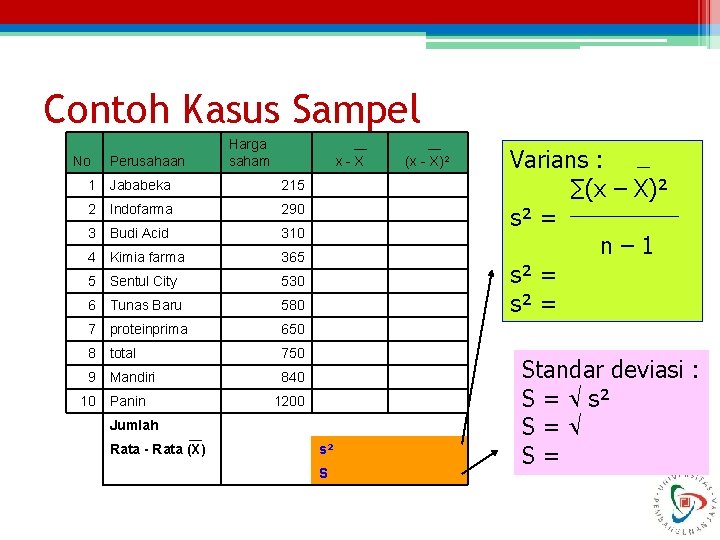
Contoh Kasus Sampel No Perusahaan Harga saham x-X 1 Jababeka 215 2 Indofarma 290 3 Budi Acid 310 4 Kimia farma 365 5 Sentul City 530 6 Tunas Baru 580 7 proteinprima 650 8 total 750 9 Mandiri 840 10 Panin 1200 Jumlah Rata - Rata (X) s² S (x - X)² Varians : ∑(x – X)² s² = n – 1 s² = Standar deviasi : S = s² S =

Ukuran Penyebaran Untuk Data dikelompokan • Range – Jarak ▫ Merupakan selisih antara batas dari kelas tertinggi dengan batas bawah dari kelas terendah • Rumusan Range = Batas kelas tertinggi – nilai terkecil

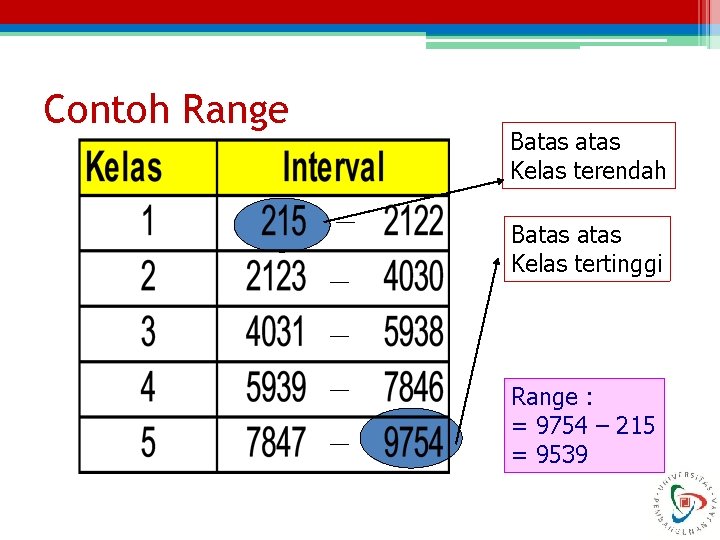
Contoh Range Batas Kelas terendah Batas Kelas tertinggi Range : = 9754 – 215 = 9539

Deviasi Rata - Rata • Rumus deviasi rata - rata f. |x - x| MD = n Rata – rata hitung data dikelompokan x = ( f. x ) / n

Contoh Kasus Kelas Interval Kelas f Titik tengah (x) 1 16 24 10 20 2 25 33 18 29 3 34 42 14 38 4 43 51 4 47 5 52 60 2 56 6 61 69 2 65 Total Rata - rata (X) f. x |x - X| f. |x - X| 50 MD = (∑f. |x - X|) / n =. . . /. . . =. . .

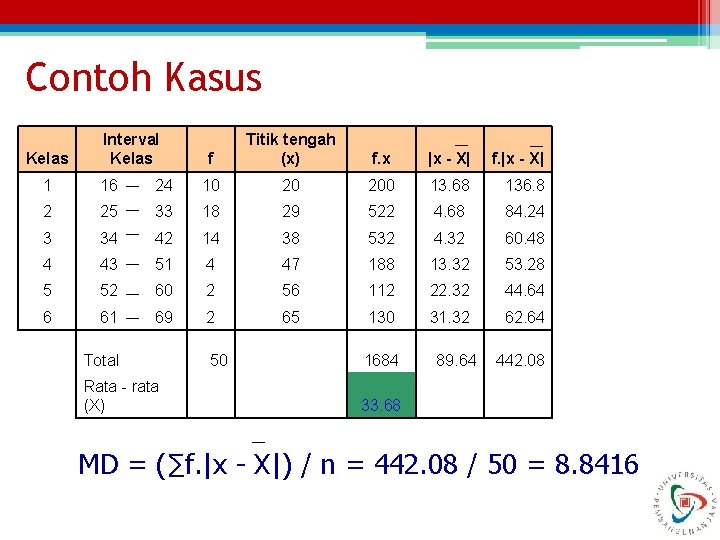
Contoh Kasus Kelas Interval Kelas f Titik tengah (x) f. x |x - X| f. |x - X| 1 16 24 10 20 200 13. 68 136. 8 2 25 33 18 29 522 4. 68 84. 24 3 34 42 14 38 532 4. 32 60. 48 4 43 51 4 47 188 13. 32 53. 28 5 52 60 2 56 112 22. 32 44. 64 6 61 69 2 65 130 31. 32 62. 64 Total Rata - rata (X) 50 1684 33. 68 89. 64 442. 08 MD = (∑f. |x - X|) / n = 442. 08 / 50 = 8. 8416

Varians dan Standar Deviasi data di kelompokan • Varians f. (x - x )2 s 2= n -1 • Standar deviasi S = s²

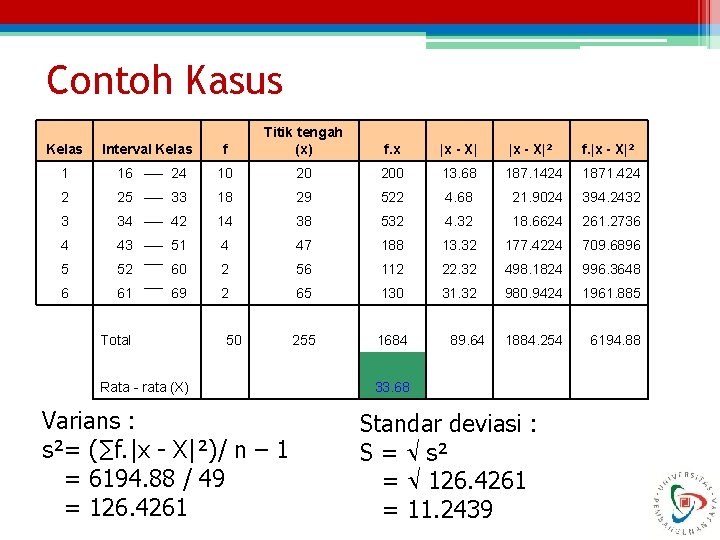
Contoh Kasus Kelas Interval Kelas f Titik tengah (x) f. x |x - X|² f. |x - X|² 1 16 24 10 20 200 13. 68 187. 1424 1871. 424 2 25 33 18 29 522 4. 68 21. 9024 394. 2432 3 34 42 14 38 532 4. 32 18. 6624 261. 2736 4 43 51 4 47 188 13. 32 177. 4224 709. 6896 5 52 60 2 56 112 22. 32 498. 1824 996. 3648 6 61 69 2 65 130 31. 32 980. 9424 1961. 885 255 1684 1884. 254 6194. 88 Total Rata - rata (X) 50 Varians : s²= (∑f. |x - X|²)/ n – 1 = 6194. 88 / 49 = 126. 4261 33. 68 89. 64 Standar deviasi : S = s² = 126. 4261 = 11. 2439

Ukuran Penyebaran Relatif • Mengubah ukuran penyebaran menjadi persentase atau ukuran relatif • Penggunaan ukuran relatif memberikan manfaat : ▫ Data mempunyai satuan penguikuran yang berbeda ▫ Data mempunyai satuan ukuran yang sama

Ukuran Penyebaran Relatif • Koefisien range • Koefisien deviasi rata-rata • Koefisien deviasi standar

Koefisien Range • Pengukuran penyebaran dengan menggunakan range secara relatif • Rumusan : KR = ( (la – Lb) / (La + Lb) ) x 100 % La : Batas data atau kelas tertinggi Lb : Batas bawah data atau kelas terendah

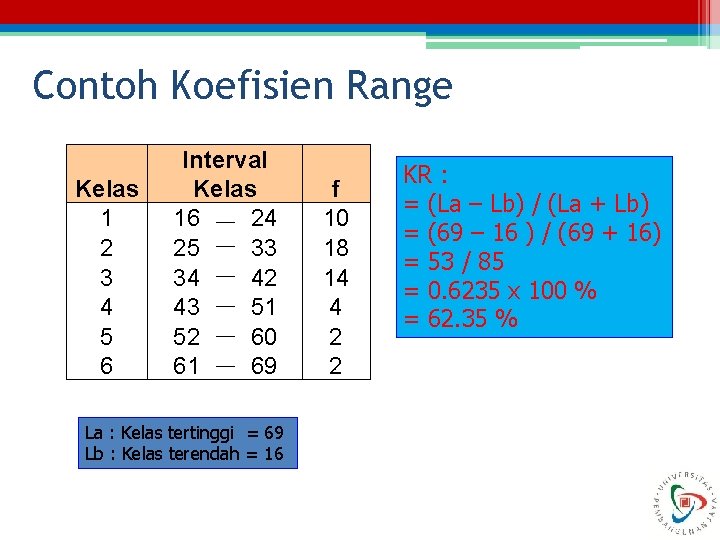
Contoh Koefisien Range Kelas 1 2 3 4 5 6 Interval Kelas 16 24 25 33 34 42 43 51 52 60 61 69 La : Kelas tertinggi = 69 Lb : Kelas terendah = 16 f 10 18 14 4 2 2 KR : = (La – Lb) / (La + Lb) = (69 – 16 ) / (69 + 16) = 53 / 85 = 0. 6235 x 100 % = 62. 35 %

Koefisien Deviasi Rata - Rata • Koefisien deviasi rata – rata ▫ Ukuran penyebaran dengan menggunakan deviasi rata-rata relatif terhadap nilai rata-ratanya atau persentase dari deviasi rata-rata terhadap nilai rata-ratanya • Rumus : KMD = [ MD / x ] x 100% MD = Deviasi rata - rata X = Nilai rata – rata data

Contoh Kasus • Data dikelompokan : ▫ MD = 8. 8416 ▫ X = 33. 68 Koefisien deviasi rata – rata : KMD = [ 8. 8416 / 33. 68 ] x 100 % = 0. 2625 x 100 % = 26. 25 %

Koefisien Standar Deviasi • Koefisien standar deviasi ▫ Ukuran penyebaran yang menggunakan standar deviasi relatif terhadap nilai rata-rata yang dinyatakan sebagai persentase • Rumus KSD = [ s / x ] x 100 % S = Standar deviasi X = Nilai rata – rata data

Contoh Kasus • Data dikelompokan ▫ Standar deviasi ▫ Rata – Rata hitung (x) = 11. 2439 = 33. 68 ▫ Nilai koefisien stnadar deviasi KSD = [ s / x ] x 100 % = [ 11. 2439 / 33. 68 ] x 100% = 0. 3338 x 100 % = 33. 38 %

Ukuran Kecondongan - Skewness • Ukuran kecondongan – kemencengan ▫ Kurva tidak simetris • Pada kurva distribusi frekuensi diketahui dari posisi modus, rata-rata dan media • Pendekatan : Jika ▫ Rata-rata = median = modus : Simetris ▫ Rata-rata < median < modus : Menceng ke kiri ▫ Rata-rata > median > modus : Menceng ke kanan

Koefisien Skewness • Sk = [µ - Mo ] / atau = 3. [µ - Md] / Contoh kasus data dikelompokan µ = 33. 68 Mo = 18 Md = 32 = 11. 2439 Sk = [33. 68 - 18 ] / 11. 2439 Sk = 15. 68 / 11. 2439 Sk = 1. 394 µ = Nilai rata – rata hitung Mo = Nilai modus Md = Nilai median = Standar deviasi Sk = {3. [ 33. 68 – 32]} 11. 2439 Sk = 5. 04 / 11. 2439 Sk = 0. 4482

Ukuran Keruncingan - Kurtosis • Keruncingan disebut juga ketinggian kurva • Pada distribusi frekuensi di bagi dalam tiga bagian : ▫ Leptokurtis ▫ Mesokurtis ▫ Platykurtis = Sangat runcing = Keruncingan sedang = Kurva datar

Koefisien Kurtosis • Bentuk kurva keruncingan – kurtosis ▫ Mesokurtik ▫ Leptokurtik ▫ Platikurtik 4 = 3 4 > 3 4 < 3 Nilai data • Koefisien kurtosis (data tidak dikelompokan) 4 = 1/n ∑(x - )4 4

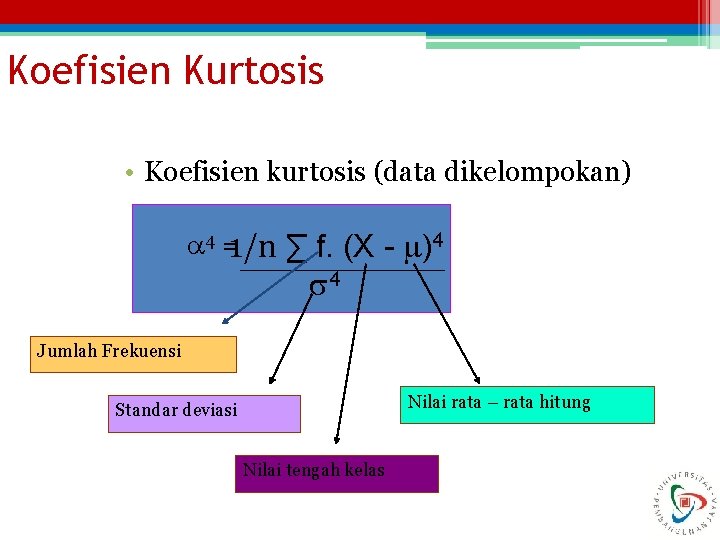
Koefisien Kurtosis • Koefisien kurtosis (data dikelompokan) 4 =1/n ∑ f. (X - )4 4 Jumlah Frekuensi Nilai rata – rata hitung Standar deviasi Nilai tengah kelas

Rata – Rata Geometrik • Digunakan untuk menghitung rata-rata laju pertumbuhan – Growth rate • Rumus : G = n (x 1. x 2. x 3. … xn ) G = [log x 1 + log x 2 +… log xn] n G = Antilog (log G)

Contoh • Data pertumbuhan suku bunga selama 5 hari, yaitu 1. 5, 2. 3, 3. 4, 1. 2, 2. 5 % • Tingkat pertumbuhan : G = [log 1. 5 + log 2. 3 +log 3. 4 + log 1. 2 + log 2. 5 ] / 5 G = [ 0. 176 + 0. 361 + 0. 531 + 0. 079 + 0. 397] / 5 G = 1. 5464 / 5 = 0. 30928 G = antilog 0. 30928 = 2. 03

Ukuran Penyebaran Lain • Range Inter-Kuartil ▫ Jarak inter-kuartil = K 3 – K 1 • Jika : ▫ Inter-kuartil : Nilainya lebih kecil ; Bahwa data dalam sampel dan populasi lebih mengelompok ke nilai rata-rata hitung (seragam) ▫ Inter-kuartil : lebih besar ; Kurang seragam

Ukuran Penyebaran Lain • Deviasi Kuartil ▫ Setengah jarak antara kuartil ke 3 dan kuartil ke 1 • Rumusan Deviasi kuartil – DK DK = [ K 3 – K 1 ] / 2 • Jika ▫ DK lebih kecil ; Rata – rata data lebih mewakili keseluruhan data

Ukuran Penyebaran Lain • Jarak persentil ▫ Selisih antara persentil ke 90 dengan persentil ke 10 • Rumusan jarak persentil - JP JP = P 90 – P 10 • Jika JP lebih besar ▫ Bahwa nilai deviasi lebih besar

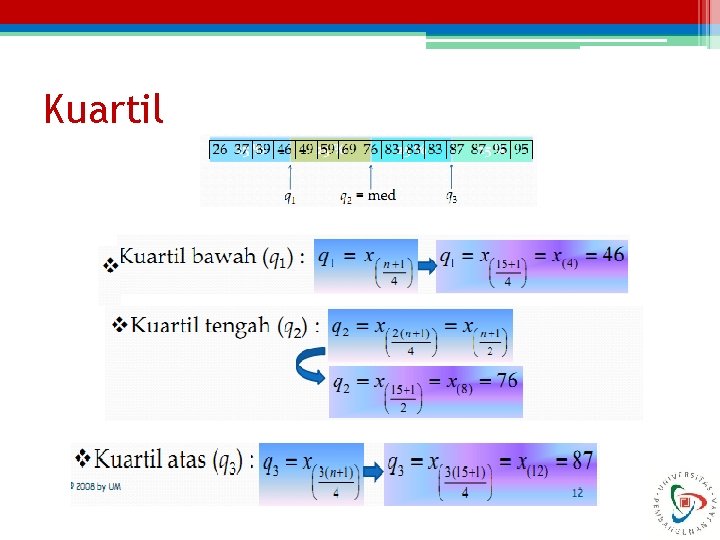
Kuartil

Jangkauan Antar Kuartil • Jangkuan Quartil Merupakan selisih antara q 1 dan q 3 yang merupakan jarak dari seluruh distribusi Quartil Jangkuan Quartil Qr= Q 3 – Q 1 Deviasi Quartil merupakan simpangan dari data dari antara Q 3 dan Q 1 Deviasi Kuartil • Qd = ½ (Q 3 – Q 1)

Latihan • Tentukan jangkauan interkuartil dan simpangan kuartil dari data berikut. 20 35 50 45 30 30 25 40 45 30 35 • Tentukan Q 1, Q 3, median (Q 2), range kuartil , dan simpangan kuartil dari data berikut. 57 49 30 46 59 43 42 47 40 45 44 56

Persentil

Jumlah & Interval Kelompok • Menentukan banyaknya kelompok • Menentukan Interval Kelompok Data diatas memiliki 5 kelompok dengan interval 14

Koefisien Variasi • Untuk membandingkan 2 kelompok dengan variabel yang sama tetapi nilai yang berbeda.

Resource • Walpole, Ronald E. , Myers, Raymond H. 2003. Ilmu Peluang dan Statistik untuk Insinyur dan Ilmuwan, Edisi 6. Bandung: Penerbit ITB.

Terima Kasih