Probabilitas dan Statistika BAB 7 Distribusi Sampling Pokok

Probabilitas dan Statistika BAB 7 Distribusi Sampling

Pokok Bahasan � Pengertian dan Konsep Dasar � Distribusi Mean-mean Sampling � Distribusi Proporsi Populasi � Distribusi Perbedaan dan Penjumlahan dari Sampling

Pengertian dan Konsep Dasar Teknik Sampling �Teknik sampling : mengambil sebagian anggota dari populasi untuk mengetahui fungsi distribusi dan karakteristik distribusi populasi tersebut. �Teknik sampling yang baik dapat menghemat biaya dan waktu tanpa harus mengorbankan keakuratan hasil-hasilnya

Pengertian dan Konsep Dasar Populasi Terhingga dan Tak Terhingga �Finite population adalah populasi yang jumlah seluruh anggotanya tetap dan dapat didaftar Cth : peserta mata kuliah probabilitas dan statistika semester gansal 2010/2011 �Infinite population adalah populasi yang memiliki anggota yang banyaknya tak terhingga Cth : pengguna telepon seluler merk “Noki*” di Indonesia
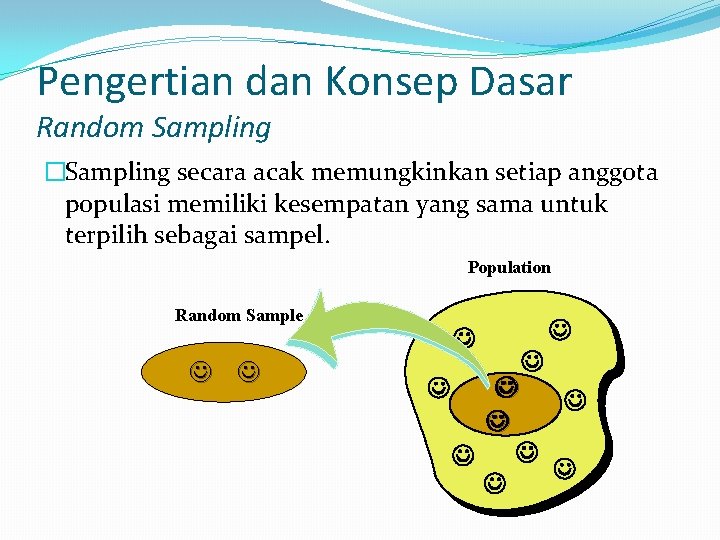
Pengertian dan Konsep Dasar Random Sampling �Sampling secara acak memungkinkan setiap anggota populasi memiliki kesempatan yang sama untuk terpilih sebagai sampel. Population Random Sample

Pengertian dan Konsep Dasar Sampling dengan dan tanpa pergantian �Sampling dengan pergantian setiap anggota dari populasi dapat terpilih lebih dari sekali �Sampling tanpa pergantian anggota populasi tidak dapat terpilih lebih dari sekali
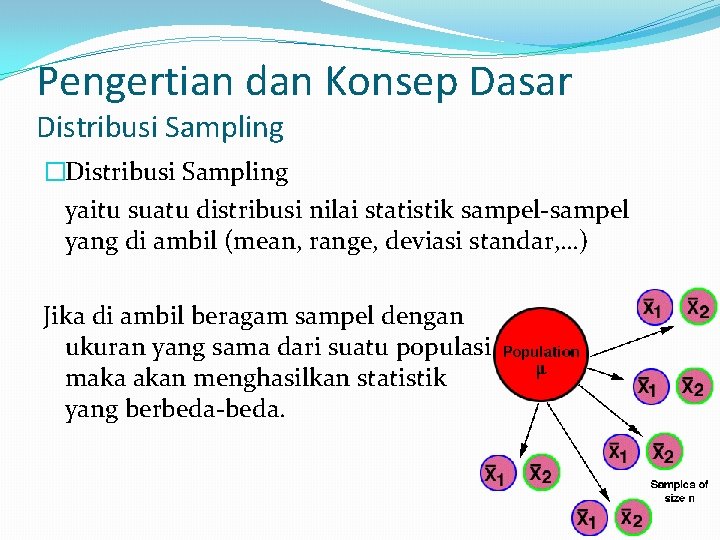
Pengertian dan Konsep Dasar Distribusi Sampling �Distribusi Sampling yaitu suatu distribusi nilai statistik sampel-sampel yang di ambil (mean, range, deviasi standar, …) Jika di ambil beragam sampel dengan ukuran yang sama dari suatu populasi maka akan menghasilkan statistik yang berbeda-beda.

Contoh Distribusi Sampling � Suatu populasi terdiri dari empat hasil pengukuran : 3 6 7 10 dari populasi ini hendak digunakan 2 hasil pengukuran sebagai sampel, distribusi mean-mean sampling (sampling distribution of the means) yang bisa dibentuk jika sampel tanpa pergantian ialah sbb : � Kemungkinan sampel : [3; 6] [3; 7] [3; 10] [6; 7] [6; 10] [7; 10] � Mean sampel yang terbentuk : 4, 5 5 6, 5 8 8, 5 � Sehingga distribusi mean sampling dari sampel-sampel yang terbentuk : Mean sampel 4, 5 5 6, 5 8 8, 5 Frekuensi 1 1 2 1 1 Probabilitas 1/6 2/6 1/6

Distribusi Mean-mean Sampling Definisi �Distribusi mean-mean sampling adalah distribusi mean-mean aritmatika dari seluruh sampel acak berukuran n yang mungkin dipilih dari sebuah populasi yang dikaji

Distribusi Mean-mean Sampling Mean dan Deviasi standar-nya � Jika sampling tanpa pergantian dari suatu populasi terhingga berukuran N : Mean dari distribusi mean sampling Mean populasi Deviasi standar dari distribusi mean sampling � Jika sampling dengan pergantian, yang berarti populasi tak terhingga : Deviasi standar populasi Ukuran sampel

Distribusi Mean-mean Sampling Contoh soal �Dalam suatu pengujian kelelahan (fatigue test), material titanium diberi pembebanan berulag sampai deteksi timbulnya retak (crack initiation). Siklus pembebanan rata -rata sampai mulai retak adalah 25000 kali dengan deviasi standar 5000. jika diuji 25 spesimen material titanium yang dipilih secara acak, berapakah : �Mean dari sampel tersebut? �Deviasi standar dari sampel tersebut?

Distribusi Mean-mean Sampling Jawaban �Mean dari sampel �Deviasi standar dari sampel

Distribusi Mean-mean Sampling Teorema Limit Pusat : �Dari suatu populasi yang memiliki distribusi normal maka distribusi mean sampling juga terdistribusi normal untuk nilai n berapapun (tidak tergantung ukuran sampel) �Dari suatu populasi yang tidak terdistribusi normal, jika ukuran sampel cukup besar (n>30), distribusi mean sampling akan mendekati suatu distribusi normal (gaussian) apapun bentuk asli distribusi populasinya.

Distribusi Mean-mean Sampling Teorema Limit Pusat 12 Distribusi X jika n > 30 10 Distribusi Populasi (tidak terdistribusi normal) Distribusi X jika n < 30 8 6 4 2 -6 -4 -2 0 0 2 4 6

Distribusi Mean-mean Sampling Contoh soal �Lima ratus cetakan logam memiliki berat rata-rata 6, 03 N dan deviasi standar 0, 4 N. Berapakah probabilitas bahwa suatu sampel acak terdiri dari 100 cetakan yang dipilih akan mempunyai berat total antara 597 sampai 600 N?

Distribusi Mean-mean Sampling Jawaban � Mean deviasi standar : � Probabilitas mean tersebut dapat dicari dengan menggunakan tabel distribusi normal standar di mana : � Maka:

Distribusi Proporsi Samping Definisi �Distribusi proporsi samping adalah distribusi proporsi-proporsi dari sejumlah sampel acak berukuran n yang mungkin dipilih dari sebuah populasi

Distribusi Proporsi Sampling Mean dan Deviasi standar-nya �Jika dalam sebuah populasi probabilitas terjadinya suatu peristiwa (probabilitas sukses) adalah π sementara probabilitas gagalnya adalah θ = 1 – π maka mean deviasi standar distribusi proporsi sampling adalah : �Jika sampling dilakukan tanpa pergantian atau populasi terhingga yang berukuran N :

Distribusi Proporsi Sampling Mean dan Deviasi standar-nya �Jika sampling dilakukan dengan pergantian atau populasinya tak terhingga, maka : Mean dari distribusi proporsi sampling Deviasi standar dari distribusi proporsi sampling Ukuran populasi Ukuran sampel Probabilitas sukses Probabilitas gagal

Distribusi Proporsi Sampling Warning! �Proporsi adalah variabel diskrit yang populasinya mengikuti distribusi binomial. Jika nilai n besar (n>30), distribusi proporsi sampling mendekati suatu distribusi normal. Untuk menentukan probabilitas dengan menggunakan tabel distribusi normal maka diperlukan faktor koreksi terhadap nilai proporsi tersebut.

Distribusi Proporsi Sampling Contoh soal �Divisi pengendalian mutu pabrik perkakas mesin mencatat bahwa 1, 5% dari bearing mengalami cacat. Jika dalam pengiriman satu kotak produk terdiri dari 100 bearing, tentukan probabilitas banyaknya bearing yang cacat sebanyak 2% atau lebih!

Distribusi Proporsi Sampling Jawaban � Mean deviasi standar : � Faktor koreksi variabel diskrit = 1/2 n = 1/200 = 0, 005 � Proporsi (2%) setelah dikoreksi, p= 0, 02 -0, 005 = 0, 015 � Maka,

Distribusi Perbedaan dari Sampling �Distribusi perbedaan dari sampling S 1 – S 2 memiliki mean deviasi standar sebagai berikut : �Dengan syarat bahwa sampel yang dipilih tidak saling terikat (saling bebas)

Distribusi Penjumlahan dari Sampling �Distribusi penjumlahan dari sampling S 1 + S 2 memiliki mean deviasi standar sebagai berikut : �Dengan syarat bahwa sampel yang dipilih tidak saling terikat (saling bebas)

Contoh �Lampu bohlam merk Phillups (1) memiliki daya tahan pakai rata-rata 2400 jam dan deviasi standar 200 jam. Sementara lampu bohlam merk Dup (2) memiliki daya tahan pakai rata-rata 2200 jam dengan deviasi standar 100 jam. Jika dari masing-masing merk dipilih 125 sampel yang diuji, berapakan probabilitas bahwa bohlam merk Phillups (1) memiliki daya tahan pakai sekurang-kurangnya 160 jam lebih lama dibandingkan bohlam merk Dup (2)?

Jawaban � Mean deviasi standar dari distribusi perbedaan sampling : � Skor z untuk perbedaan mean 160 jam adalah : � Jadi, probabilitas yang akan ditentukan adalah :
- Slides: 26