PROBABILISTIC ROTATION PERIODS WITH GAUSSIAN PROCESSES RUTH ANGUS

PROBABILISTIC ROTATION PERIODS WITH GAUSSIAN PROCESSES RUTH ANGUS, SUZANNE AIGRAIN & DAN FOREMAN-MACKEY ruthangus@astro. ox. ac. uk // @ruthangus // ruthang. us // github. com/ruthangus

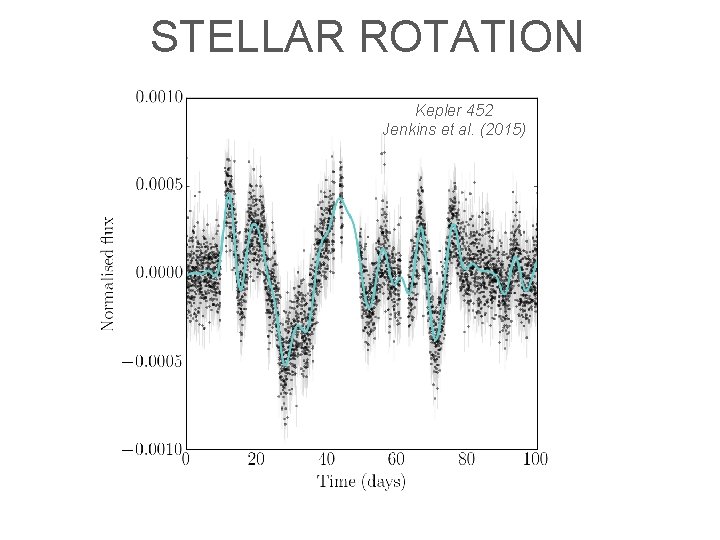
STELLAR ROTATION Kepler 452 Jenkins et al. (2015)

PERIODOGRAMS. STANDARD PRACTISE e. g. Reinhold, Reiners & Basri (2013) AUTOCORRELATION FUNCTIONS. e. g. Mc. Quillan et al. (2013) @RUTHANGUS

FORMALLY: GAUSSIAN PROCESSES Perfect for describing quasiperiodic, non sinusoidal stochastic processes. If the probability of obtaining a dataset is an N-dimensional Gaussian, where N is the number of data points, then the dataset was produced by a GP. USEFULLY: A distribution over functions. A semi-parametric model. For smoothly varying functions @RUTHANGUS

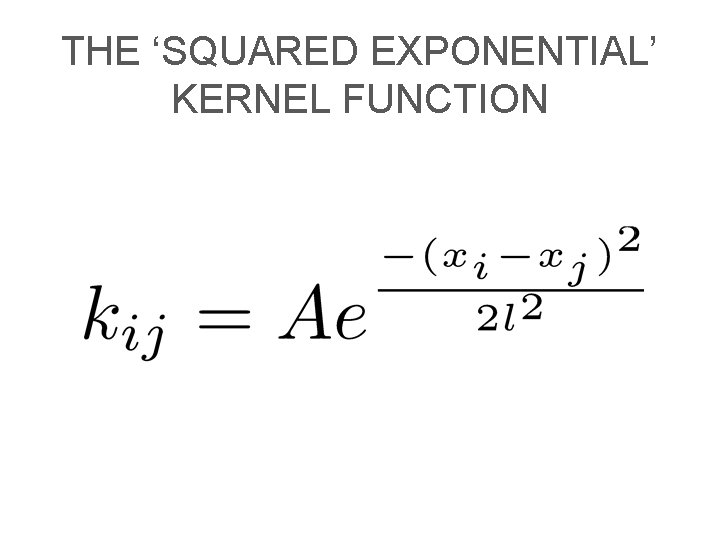
THE ‘SQUARED EXPONENTIAL’ KERNEL FUNCTION

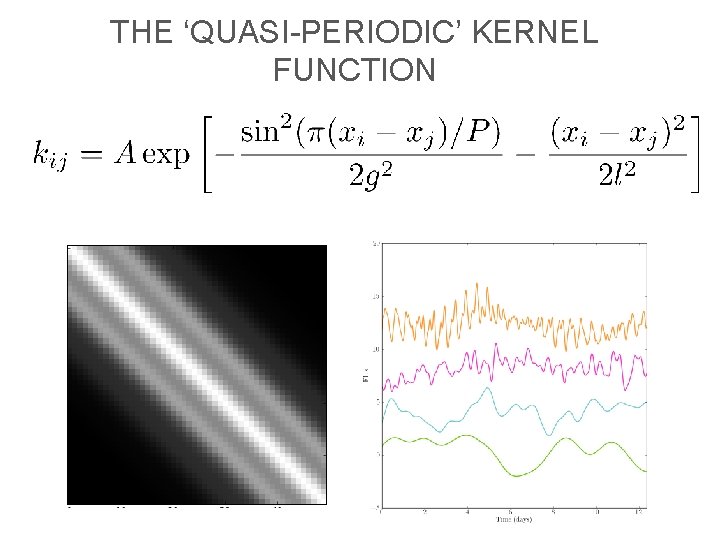
THE ‘QUASI-PERIODIC’ KERNEL FUNCTION

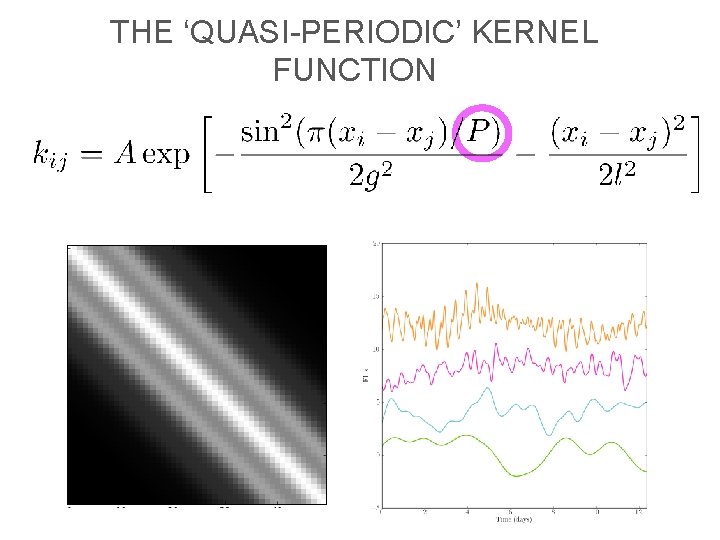
THE ‘QUASI-PERIODIC’ KERNEL FUNCTION

A ‘DROP-IN’ LIKELIHOOD FUNCTION REPLACEMENT

A ‘DROP-IN’ LIKELIHOOD FUNCTION REPLACEMENT

A ‘DROP-IN’ LIKELIHOOD FUNCTION REPLACEMENT

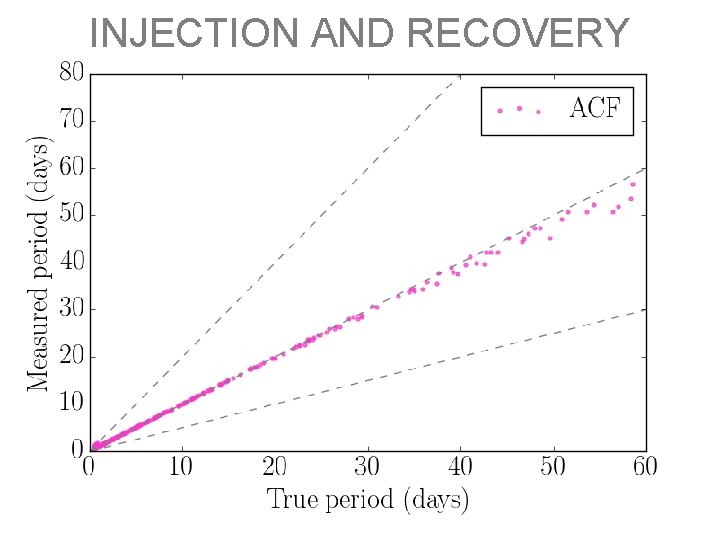
INJECTION AND RECOVERY

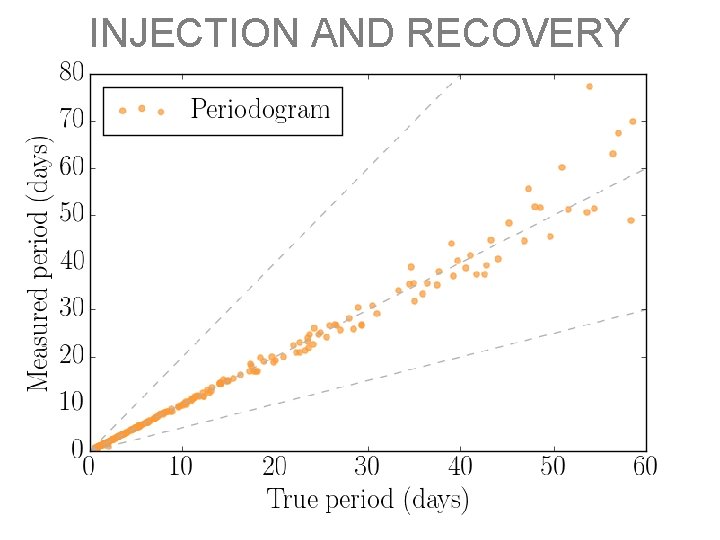
INJECTION AND RECOVERY

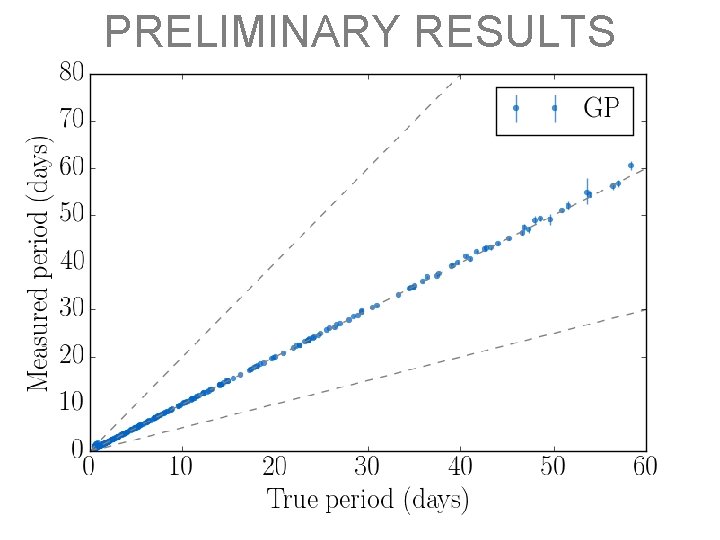
PRELIMINARY RESULTS

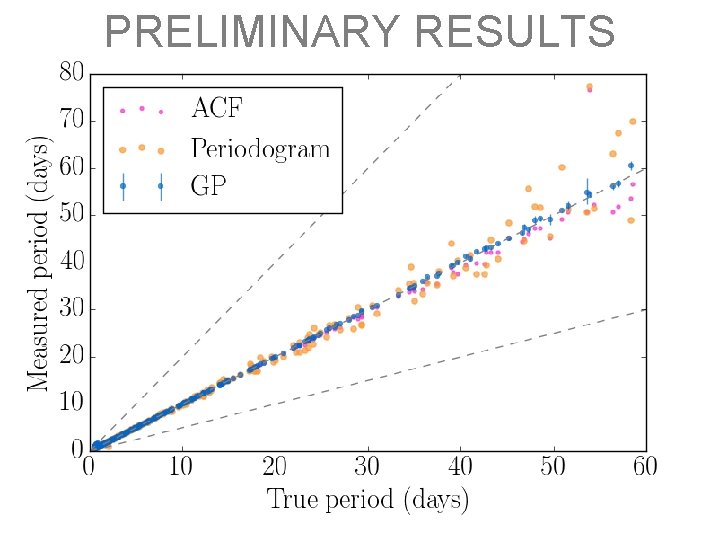
PRELIMINARY RESULTS

github. io/ruthangus/GProtation

Computation time (dfm. io/george) Data must be Gaussian distributed: NO OUTLIERS! SUMMARY More accurate periods. More representative uncertainties. Directly use posterior samples for your hierarchical inference. @RUTHANGUS